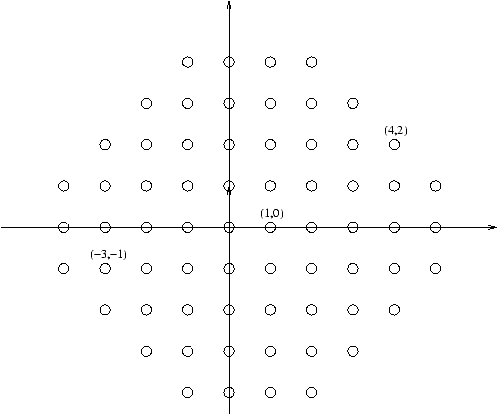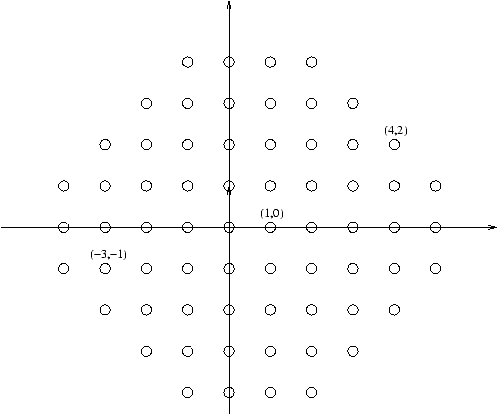Analysis Of Algorithms
Analysis Of Algorithms
 Class notes
Class notes
 Combinatorics
Combinatorics
Document also available in PDF, Postscript, DVI, Text, LaTeX, LyX.
Chapter 1 Sets (section 3.1 )
1.1 Introduction
Problem p 161
Goal:
-
Introduce the formalism of set theory
- Use it to solve counting problems
1.2 Sets and basic manipulations of sets
1.2.1 Definition
Définition 1
A set A is a collection of objects.
Defining property: you can ask whether an object a belongs to A
or not.
Objects or elements: a,b,c,....
Sets: A,B,C,....
Predicates:
-
ain S: a belongs to S, or a is an element of S, or
S contains a;
- anot in S: a does not belong to S.
Two sets A and B are equal (A=B) if they contain the
same elements:
(for all x)(xin A)<=>(xin B)
1.2.2 How to define a set S?
You have to describe which elements are in the set S and which
are not.
-
List the elements of the set S:
S:={ a,b,c}
ain S is true, whereas din S is false.
The order and the repetition are irrelevant:
{ a,b,c}={ a,b,b,b,c}={ c,b,a}
Note that a and { a} are two different things. The first is
the object a, whereas the second one is the set containing a,
and no other elements.
- Provide a predicate which determines which element are in S:
S:={ x | P(x)}
S:={ x | x is an integer and 3<x<=7}
5in S is true, whereas 3not inS, and no car belongs to A.
- Use a recursive definition, as for the set of well formed formulas:
S contains basic propositions A,B,C,...
If P and Q belong to S, then P', P/\ Q, P\/ Q,
P-> Q, P<-> Q also belong to S.
Some usual sets:
-
The empty set:
Ø:={ x | false}
- Numbers:
N:={ x | x is a non negative integer }
Z:={ x | x is an integer }
Q:={ x | x is a rational number }
R:={ x | x is a real number }
C:={ x | x is a complex number }
S*:={ x | xin S and x!=0}
S+:={ x | xin S and x>=0}
1.2.3 Relationships between sets
Exercice 1
[, Exercise 10 p. 117]
R:={1,3,pi,4,1,9,10}, S:={{1},3,9,10}
T:={1,3,pi}, U:={{1,3,pi},1}
-
Sincluded in or equal to R?
- 1in R?
- 1in S?
- 1included in or equal to U?
- {1}included in or equal to T?
- {1}included in or equal to S?
- Tincluded in R?
- {1}in S?
- Øincluded in or equal to S?
- Tincluded in or equal to U?
- Tin U?
- Tnot in R?
- Tincluded in or equal to R?
- Sincluded in or equal to{1,3,9,10}?
1.2.4 The powerset of a set
The powerset (S) of a set S is the set of all subsets of
S.
Exemple 1
What are the elements of the following powersets ?
-
({1,2})=
- ({1})=
- (Ø)=
Exercice 2
What is the size of (S) if S has n elements ?
1.2.5 Binary and unary operations
Définition 2
¤ is a unary operation on a set S if for every
element x of S, ¤ x exists, is unique and is a member
of S.
¤ is a binary operation on a set S if for every
ordered pair (x,y) of elements of S, x¤ y exists, is
unique and is a member of S.
Examples:
-
is +a binary operation on N ?
- is +a binary operation on {0,1,2}?
- is ×a binary operation on {0,1}
- is -a binary operation on N ?
- is /a binary operation on Z ?
- are +,-, and ×binary operations on Q ?
- are +,-, ×and /binary operations on Q*?
- is (x)1/2 a unary operation on R+ ?
- are /\, \/, ->, ', ... operations
on { true,false}? on wff ?
A binary operation can be defined by its multiplication table.
Exemple 2
({ true,false},/\)
| /\ |
false |
true |
| false |
false |
false |
| true |
false |
true |
An operation does not necessarily need to have a particular meaning.
Exemple 3
({2,5,9},¤)
| ¤ |
2 |
5 |
9 |
| 2 |
2 |
5 |
2 |
| 5 |
2 |
9 |
5 |
| 9 |
9 |
2 |
5 |
5¤9=?
1.3 Operations on sets
1.3.1 The universe of discourse
We have seen operations on numbers, or other objects.
We can also define operations on sets (union, intersection, ...).
We need a set that contains all the sets we want to deal with.
It would be tempting to consider the set of all sets.
Problem 1
Let S be the set of all sets that does not contain themselves.
Does S contain itself ?
-
if S does not contain itself, then it contains itself !
- if S contains itself, then it does not contain itself !
There is a strange loop here which yields a contradiction: S cannot
exist.
For a similar reason, the set of all sets cannot exist.
See Gödel Esher Bach[] for a lot of similar
fun stuff with strange loops.
That's been a major source of trouble and work a century ago, when
mathematicians tried to define a strong basis for set theory.
To be safe, we always work inside a set big enough to contain all
the sets we need, but small enough to avoid the strange loop above.
Définition 3
This set is the universal set, or the universe of discourse.
We define operations on the powerset of the universal set.
1.3.2 Union, intersection, complement and Cartesian product
We define operations on subsets of the universe of discourse.
Définition 4
The union
of A and B is the set:
Aunion B:={ x | xin A or xin B}
Définition 5
The intersection
of A and B is the set:
Aintersect B:={ x | xin A and xin B}
Définition 6
The complement
of A is the set:
A':={ x | xnot in A}
Définition 7
The set difference
of A and B is the set:
A-B:={ x (xin A) and (xnot in B)}
Définition 8
The Cartesian product
(or cross product
) of A and
B is the set:
A× B:={(x,y) | xin A,yin B}
Notation 2
A2=A× A is the set of all ordered pairs of elements of
A;
An=A×···× A is the set of all n-uples of elements
of A.
Définition 9
Venn diagrams.
Exercice 3
Let
A:={1,2} and
B:={2,3,4}.
-
Aunion B=,
- Aintersect B=,
- A-B=,
- A'= (assuming that the universe of discourse is {1,2,3,4}),
- A× B=,
- A3=.
Exercice 4
Let A be a set of size n, and B a set of size m.
-
what is the size of Aunion B:
- what is the size of Aintersect B:
- what is the size of A' ?
- what is the size of A× B :
1.3.3 Set identities
Proposition 1
Let A and B be to sets. Then,
Aintersect B=Bintersect A (commutative property)
Proof.
xin Aintersect B
<=>(xin A)/\(xin B) by definition of intersect
<=>(xin B)/\(xin A) by commutativity of /\
<=> xin Bintersect A by definition of intersect
The commutativity of intersectderives directly from the commutativity
of /\.
All identities on logic operators induce identities on set operators.
Proposition 2
Let A, B, and C be two sets. Then,
Aunion B=Bunion A (commutative property)
Aintersect B=Bintersect A (commutative property)
(Aunion B)union C=Aunion(Bunion C)=Aunion Bunion C (associative property)
(Aintersect B)intersect C=Aintersect(Bintersect C)=Aintersect Bintersect C (associative property)
Aunion A'=S (complement, S is the universe of discourse)
Aintersect A'=Ø (complement)
(Aunion B)'=A'intersect B' (de Morgan's)
(Aintersect B)'=A'union B' (de Morgan's)
A-B=Aintersect B'
1.4 Countable and uncountable sets
1.4.1 Enumerations
If a set S has k elements, these can be listed one after the
other:
s1,s2,...,sk
Définition 10
s1,s2,...,sk is called an enumeration of the
set S.
Exemple 4
1,5,4,3, 5,1,3,4, and 4,1,3,5 are enumerations of the set
{1,5,4,3}.
When a set S is infinite, you can not enumerate all of it's elements
at once.
However, some times, you can still pickup a first element s1,
then a second s2, and so on forever. This process is an enumeration
of the elements of S if:
-
Any element of S gets enumerated eventually;
- No element is enumerated twice.
Exemple 5
0,1,2,3,4,... is an enumeration of the non-negative integers.
1.4.2 Denumerable and Countable sets
Définition 11
A infinite set S is denumerable
if it has an enumeration
s1,s2,...,sn,...
A set S is countable
if it's either finite or denumerable.
Exemple 6
Are the following sets countable ?
-
The set of all students in this class.
- The set N of the non-negative integers (enumeration: 0,1,2,3,4,...);
Actually, the order does not need to be logical.
This is a perfectly legal enumeration: 0,10,5,11,4,2,17,2,1,28,3
- The set of the even integers (enumeration: ;
- The set of the prime integers (enumeration: ;
- The set Z of the integers (enumeration: );
- The set N×N
(e.g. all points in the plane with non-negative integer coordinates):


- Enumeration: (0,0),(0,1),(1,0),(2,0),(1,1),(0,2),(3,0),...
- The set Z×Z of all points in the plane with integer coordinates:
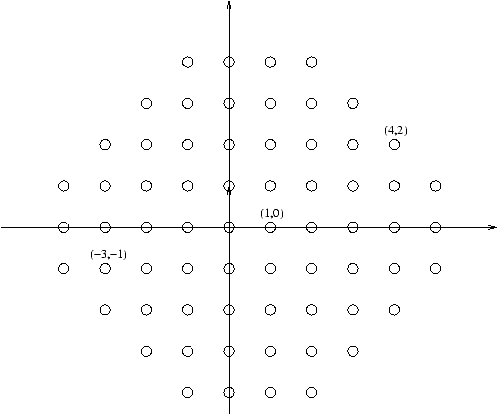
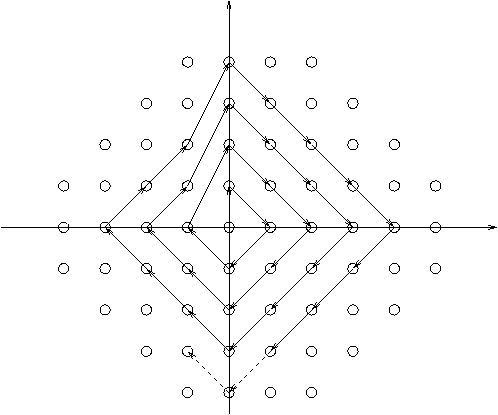
Enumeration: (0,0),(0,1),(1,0),(0,-1),(-1,0),(2,0),...
- The set Q of rational numbers:
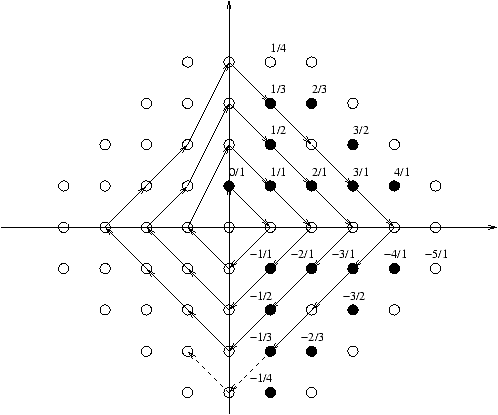
Théorème 1
The following sets are countable:
-
Any subset Aincluded in B of a countable set B.
- The union Aunion B of two countable sets A and B is countable.
- The union A1union A2union···union Ai of a finite number
i of countable sets A1,...,Ai.
- The union A1union A2union···union Aiunion···of a countable
number of countable sets.
- The cross product A× B of two countable sets A and B
is countable.
- The cross product A1×···× Ai of a finite number
of countable sets A1,...,Ai.
Proof.
Enumerations of those sets can be constructed in the following way:
-
Enumerate the elements of B, and ignore those that are not in A.
- Enumerate the elements of A and B alternatively (a1,b1,a2,b2,...).
- Induction, using 2.
- As for N×N: a1,1,a2,1,a1,2,a3,1,a2,2,a1,3,...
(ai,j is the jth element of Ai).
- As for N×N: (a1,b1),(a1,b2),(a2,b1),(a1,b3),(a2,b2),(a3,b1),....
- Induction, using 5.
1.4.3 Uncountable sets ?
Remarque 1
All the sets we have seen so far are countable.
Problem 1
Are there any uncountable sets ?
Théorème 2
(Cantor) R is uncountable.
Lemme 1
Any real number
xin[0,1) can be written uniquely in decimal form:
x=0.d1d2d3d4··· di···,
where the
di are digits between 0 and 9, and the sequence
does not end by an infinite number of 9.
Exemple 7
Here is how some classical numbers can be written:
-
0=0.0000···
- 0.5=0.50000···
- 0.5=0.49999··· (Same number as above, we don't use this form)
- 1/3=0.333333···
- pi=3.141592653···
Let's jump to the proof of the theorem, without detailing the proof
of this lemma.
Proof.
(Of the theorem): Cantor diagonalization method.
It's sufficient to prove that [0,1) is not countable.
Let's do this by contradiction: assume [0,1) is countable.
Let s1,s2,...,si,... be an enumeration of [0,1).
Goal: construct an element which is not in this enumeration.
Using the lemma, we can write the si as follow:
|
|
| s1 |
= |
0, |
|
d1,2 |
d1,3 |
d1,4 |
d1,5 |
··· |
| s2 |
= |
0, |
d2,1 |
|
d2,3 |
d2,4 |
d2,5 |
··· |
| s3 |
= |
0, |
d3,1 |
d3,2 |
|
d3,4 |
d3,5 |
··· |
| s4 |
= |
0, |
d4,1 |
d4,2 |
d4,3 |
|
d4,5 |
··· |
| s5 |
= |
0, |
d5,1 |
d5,2 |
d5,3 |
d5,4 |
|
··· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
|
We want to construct an element x which is not in this enumeration.
Let's look at an example:
|
|
| s1 |
= |
0, |
|
5 |
7 |
3 |
5··· |
| s2 |
= |
0, |
0 |
|
4 |
7 |
3··· |
| s3 |
= |
0, |
4 |
5 |
|
0 |
3··· |
| s4 |
= |
0, |
9 |
7 |
3 |
|
7··· |
| s5 |
= |
0, |
4 |
3 |
8 |
1 |
|
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
· |
·
·
··
·
· |
| |
|
|
|
|
|
|
|
| x |
= |
0, |
0 |
1 |
0 |
0 |
1··· |
|
The trick : let xi=1 if di,i=0 and xi=1 else.
Then, x!= s1. But also, x!= s2, x!= s3, ...
Therefore x is indeed never enumerated! Contradiction!
Conclusion: [0,1) is not countable.
Remarque 2
We can deduce that many sets like C, or [5.3,10) are uncountable.
A similar proof can be used to prove that many other sets are uncountable.
This includes the set of all infinite strings, or the set (N)
of all subsets of N.
Résumé 2
We have a hierarchy of bigger and bigger sets:
-
The empty set
- Finite sets (the empty set, sets with 1 element, sets with 2
elements, ...)
- Denumerable sets: N, Z, Q, ...
- Uncountable sets: R, C, ...
- ...
Problem 3
Is there any set bigger than N and smaller that R? Nobody
knows!
1.5 Conclusion
We are now done with basic properties of sets. We have seen enough
formalism
to go on to the next section, Combinatorics:
How to count the objects in a finite set ?

 Analysis Of Algorithms
Analysis Of Algorithms
 Class notes
Class notes
 Combinatorics
Combinatorics
Sets /
CSM MACS-358 /
Nicolas M. Thiéry
Last modified: Fri Jan 19 13:12:17 2007