TP de mathématiques

Exercice 1  

1. Calculer 1+1, 2*2, 2³⁰, 10!, 5/9. Que constate-t'on?
2. Calculer √2, puis (√2)² (indication: consulter l'aide avec ?sqrt). En calculer des approximations numériques (cf. ?float). Faire varier la précision en jouant avec DIGITS := 200. Puis réinitialiser à 10 chiffres de précision.
3. Calculer sin(3.14), sin(π), sin(π/3) (cf. ?sin, ?PI). Que constate-t'on?

Exercice 2  

1. Essayer la commande: (f+g) ( x + y ). Comparer avec (f+g) * (x+y). Conclusion?
2. Développer (x+3)(x−2) (cf. ? expand), et stocker le résultat dans une variable p (cf. ?:=).
3. Refactoriser le résultat (cf. ? factor).
4. Utiliser solve pour retrouver les racines de p.
5. Factoriser x²−2 et chercher ses racines.
6. Factoriser p := x⁷−3x²+x+1 et chercher ses racines. Interpréter.
7. Évaluer p en x=0, x=2, x=π, x=y² (cf. ? |).
8. Tracer le graphe de la fonction x↦ p(x) de R dans R (cf. ? plot::Function2d). En utilisant ce graphe et la fonctionnalité de zoom, donner le nombre de racines de p.
9. Calculer numériquement les racines de p (cf. ? solve, ? float).

Exercice 3  

1. Calculer arccos(1), arccos(−1), arccos(√2/2), arccos(−x).
2. Calculer la dérivée de arccos, puis en tracer le graphe (cf. ? diff, ? plot::Function2d)
   
   
3. Calculer la dérivée par rapport à x des expressions suivantes:
   1. 3sin(x)+x⁵ − 1/(1+x²+3x⁵)
   2. f(x) + g(x)
   3. f(x) g(x)
   4. f(x)/g(x)
   5. (f∘ g) (x) (cf. ?@)
   
   
   
4. Calculer symboliquement puis numériquement les intégrales suivantes (cf. ? int):
   1. ∫_x=0^π/2 cos(x)/1+sin(x) dx.
   2. ∫_x=0¹ dx/e^x2 + 1.
   Que constate-t'on?
   
   
5. Calculer les primitives des expressions suivantes, puis les redériver pour vérifier le résultat:
   1. x².
   2. 1/4 e^x + e^−x + 4.
   3. 1/e^x2 + 1.
   Que constate-t'on?

Exercice 4   Résoudre en fonction de m le système d'équations:

Exercice 5   La première application concerne la modélisation de la dynamique des populations, telle qu'étudiée en écologie. Le cas d'école que nous allons considérer n'est pas nouveau, puisqu'il a été proposé en 1202 par Leonardo Pisano comme problème récréatif dans un de ses ouvrages, le Liber Abaci.

Possédant initialement un couple de lapins, combien de couples obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ?

Nous allons considérer un modèle très simple, dans lequel on notera f_n le nombre nombre de paires de lapins en fin de n-ième mois, dans une population idéale telle que:

• le premier mois, il y a juste une paire de lapereaux,
• les lapereaux ne sont pubères qu'à partir du deuxième mois,
• chaque mois, toute paire susceptible de procréer engendre effectivement une nouvelle paire de lapereaux,
• les lapins ne meurent jamais.

1. Donner la relation de récurrence satisfaite par la suite f_n.
2. Donner le surnom de Leonardo Pisano.
3. Nous souhaitons maintenant calculer f_n pour n relativement grand. Pour cela, nous allons mettre le problème sous forme matricielle en notant pour n>=2, F_n:=(

   fn

   fn−1

   ).
   1. Donner F₂, et déterminer une matrice M telle que F_n+1=M F_n pour n≥ 2.
   2. À l'aide d'une boucle for, calculer f₁₀₂₆ et f₆₅₆₃₆.
   3. Calculer F₁₀₂₆=M¹⁰²⁴ F₂ et F₆₅₆₃₈=M⁶⁵⁶³⁶ F₂. À votre avis, comment s'y prend la machine?
   4. Pouvez-vous l'égaler en utilisant uniquement des produits de matrices?
   5. Évaluer le nombre d'opérations arithmétiques (+, * sur les coefficients des matrices) nécessaires pour calculer M²ⁿ.
   6. Utiliser la commande time pour comparer le temps de calcul de M²²⁰ et de float(M)²²⁰. Interpréter.
   7. Calculer numériquement f_2²⁰, f_2²³, f_2²⁴. Interpréter.
4. Nous cherchons maintenant donner une formule exacte pour f_n. Pour cela, on va diagonaliser la matrice M.
   1. Vérifier que M²−M−I₂=0. Comparer avec le résultat de linalg::minimalPolynomial(M,z).
   2. Soit v un vecteur non nul et λ un réel tels que Mv=λ v. Montrer que λ²−λ−1=0. En déduire les deux valeurs λ₁<λ₂ de λ possibles (cf. solve; expérimenter avec op pour extraire les valeurs du résultat de solve). Donner leurs valeurs numériques (cf. float).
   3. Chercher deux vecteurs non nuls v₁ et v₂ tels que Mv₁=λ₁ v₁ et Mv₂=λ₂ v₂. On pourra utiliser la commande linalg::nullspace, en remarquant que l'équation Mv=λ v est équivalente à (M−λ I₂) v = 0.
   4. λ₁ et λ₂ sont les valeurs propres de M, et v₁ et v₂ des vecteurs propres correspondants. comparer avec le résultat des commandes: linalg::eigenvalues(M) et linalg::eigenvectors(M).
   5. Soit B la base canonique de R², et B' la base (v₁, v₂). Donner la matrice de passage P de B à B'. Vérifier que P est inversible (cf. linalg::det), puis calculer la matrice de passage de B' à B.
   6. Calculer au moyen des formules usuelles de changement de base la matrice M' dans B' de l'application qui a pour matrice M dans la base B (attention: le symbole ' dénote la dérivation; utiliser par exemple M1 pour nommer M'). Essayer les commandes expand, simplify, radsimp pour simplifier le résultat. Interpréter.
   7. Calculer M'ⁿ. En déduire Mⁿ, puis une formule close pour f_n.
   8. Utiliser cette formule pour calculer de manière exacte puis numériquement quelques valeurs de f_n pour n grand (voir ?radsimp).

Exercice 6   La deuxième application concerne le test automatique de programmes informatiques. À quelques simplifications près, le modèle que l'on va étudier est utilisé dans le monde industriel (voir http://www.lri.fr/~gouraud/recherche.fr.html), et les questions que l'on va rencontrer sont significatives des problèmes rencontrés dans le monde du test.

Dans ce modèle, un programme est décrit par un graphe de contrôle. Par exemple, le programme suivant:

decompositionBinaire :=
proc(nombre)
begin
    resultat := [];
    while nombre>0 do
        if nombre mod 2 = 1 then
             resultat := append(resultat,1);
             nombre := nombre-1
        else
             resultat := append(resultat,0)
        end_if;
        nombre := nombre div 2;
    end_while;
    resultat;
end_proc:

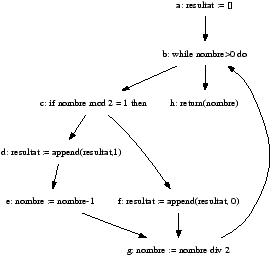
sera décrit par le graphe suivant:



Une trace d'exécution est alors une suite de sommets consécutifs allant du sommet a au sommet h dans ce diagramme. Par exemple, en appliquant ce programme au nombre 5, on obtient la trace (a,b,c,d,e,g,b,c,f,g,b,c,d,e,g,b,h). Vous pouvez le vérifier à la main, ou en utilisant la commande debug(decompositionBinaire(5)). La longueur d'une trace est le nombre de sommets parcourus, soit 17 dans l'exemple précédent.

Le principe de cette méthode de test est d'étudier les traces d'exécutions possibles, et de déterminer si elles sont correctes. Ici, notre objectif est simplement de compter le nombre h_k de traces d'exécutions de longueur n, afin de déterminer jusqu'à quelle longueur on peut envisager de faire du test exhaustif. En particulier, on ne se préoccupera pas ici des valeurs des variables du programme. Formellement, le problème est de compter les chemins dans un graphe orienté.

1. Lister toutes les traces d'exécutions de longueur inférieure à 17.
2. On considère le vecteur

   Vn:=

   ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ an bn cn dn en fn gn hn ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠

   (1)

   où c_n compte le nombre de traces d'exécutions du sommet a au sommet c de longueur n, et similairement pour a_n,...,h_n
   1. Calculer les vecteurs V₀, V₁, V₂, V₃, V₄.
   2. Donner une formule de récurrence permettant d'exprimer g_n en fonction de a_n−1,...,h_n−1. Exprimer de même les autres coordonnées de V_n.
   3. Déterminer une matrice M telle que V_n=MV_n−1.
   4. Calculer le nombre de traces d'exécutions de longueur 1024. Évaluer très grossièrement le temps nécessaire pour tester toutes ces traces, sur un ordinateur à 2GHz (on admettra que le traitement de chaque sommet prend environ 100 cycles d'horloge).
3. Pour donner une formule approximative pour h_n, on va procéder comme dans l'exercice précédent en diagonalisant la matrice M.
   1. Calculer les valeurs propres de M à l'aide de la commande linalg::eigenvalues(M). Interprétation? Calculer le polynôme minimal de M avec linalg::minimalPolynomial
   2. Pour simplifier, nous nous contenterons de faire un calcul numérique approché, en considérant la matrice de flottants float(M).
   3. Calculer numériquement les vecteurs propres de M.
   4. En déduire une base B' de Rⁿ dans laquelle M est diagonale.
   5. Calculer les matrices de changement de base.
   6. Calculer la matrice M' correspondant à M dans cette nouvelle base.
   7. Calculer M'ⁿ, puis Mⁿ, puis V_n puis h_n.
   8. Donner une approximation de h_n sous la forme aⁿ.
   9. Jusqu'à quelle valeur de n peut-on raisonnablement faire du test exhaustif?

points := [matrix(point)
           $ point in [[   0, 1755], [1980,  180], [2070, 1260], [3150,  720],
                       [2340, 3240], [4095, 1125], [3060, 3735], [4860, 1260],
                       [4050,  900], [4590,  900], [7650, 2070], [6300, 1890],
                       [5130, 1395], [3645, 4275], [3735, 4320], [5175, 1485],
                       [5445, 1620], [4950, 3105], [5355, 3285], [6795, 2250],
                       [7695, 2295], [4590, 4860], [4365, 4725], [4860, 3915],
                       [4590, 3780], [3915, 4455], [2790, 3780], [3060, 2880],
                       [2070, 3645], [1710, 2655], [2970, 990],  [1440, 2295],
                       [1845, 450], [1035, 2160]]];

plot(plot::Polygon2d(points))

Exercice 7   Soit M une matrice M de dimension 2× 2, et ϕ l'application linéaire de R² dans R² correspondante. Notre objectif est d'interpréter géométriquement la transformation ϕ lorsque cela est possible.

Considérons d'abord la matrice:

    M := matrix ( [ [ 0,1],
                    [ 1,0] ]):

Étant donné un vecteur v de R², l'image ϕ(v) de v par ϕ peut être obtenue en calculant M*v. Calculer l'image des vecteurs de la base canonique de R².

Pour visualiser l'image du polygone par ϕ, il suffit donc de faire:

plot(plot::Polygon2d([ M*v $ v in points]))

1. Quelle est la transformation géométrique effectuée par ϕ?
2. Même question pour les matrices suivantes:

   
       M := matrix ( [ [-1, 0],
                       [ 0,-1]])
   

   
       M := matrix ( [ [ 4, 0],
                       [ 0, 1]])
   

   
       M := matrix ( [ [ 1, 0],
                       [ 0, 1]])
   

   
       M := matrix ( [ [ 1, 0],
                       [ 0,-1]])
   

3. L'animation suivante permet de visualiser l'effet de la matrice

   
       M := matrix ( [ [ 1, 0],
                       [ 0, 1/2^n]])
   

   lorsque n tend vers l'infini.

   
   plot(plot::Polygon2d([ matrix([[1,0],[0,1/2^n]])*v $ v in points], n=1..10))
   

   Quelle est la transformation géométrique pour la matrice limite

   
       M := matrix ( [ [ 1, 0],
                       [ 0, 0]])
   

4. Chercher la matrice de l'application linéaire ϕ qui effectue une homothétie (zoom) de facteur 2, et plus généralement de facteur lambda. Vérifier le résultat en visualisant le polygone transformé.
   
   
5. En vous inspirant de l'exemple précédent, construire une animation où le polygone grossit progressivement.
6. Chercher la matrice de l'application linéaire ϕ qui effectue une rotation d'un quart de tour dans le sens trigonométrique.
   
   
7. Chercher la matrice de l'application linéaire ϕ qui effectue une rotation d'angle θ dans le sens trigonométrique (indication: chercher l'image par ϕ des vecteurs de la base canonique).
   
   
8. Construisez une animation où le polygone tourne autour du point de coordonnées (0,0).
9. Même chose, en faisant grossir progressivement le polygone au fur et à mesure qu'il tourne.
10. Chercher la matrice de l'application linéaire ϕ qui envoie le vecteur b₁:=

    1

    1

    sur 2b₁, et b₂:=

    1

    −1

    sur 1/2 b₂ (indication: donner la matrice de ϕ dans la base (b₁,b₂), puis appliquer les formules de changement de base pour obtenir sa matrice M dans la base canonique).

Exercice 8   Toutes les transformations que nous avons rencontrées pour l'instant sont linéaires; en particulier le vecteur 0 reste inchangé.

1. Quelle opération matricielle pourrait-on utiliser pour décaler le polygone de 1000 points vers la gauche?
2. Plus généralement pour effectuer une translation le long d'un vecteur de coordonnées (x,y)?
3. Construire une animation où le polygone part vers la droite de plus en plus vite.
4. Ce que nous venons de faire, c'est de nous placer dans une classe plus grande de transformations: les transformations affines. Celles si sont de la forme v ↦ M v + u, où M est une matrice 2× 2, et u un vecteur de R².
5. Chercher la transformation affine correspondant à la rotation d'angle 45 degrés autour du centre du polygone.
6. Construire une animation où le polygone tourne, grossit et se déplace simultanément.

Exercice 9   Nous voulons maintenant animer le polygone en 3D. Afin de comprendre la mécanique interne, nous n'utiliserons pas les possibilités natives de MuPAD. Pour simplifier, nous nous contenterons ici de perspective cavalière.

1. Pour plonger le polygone dans R³, nous pouvons utiliser l'application linéaire de R² dans R³ qui envoie les deux vecteurs de la base canonique de R² sur les deux premiers vecteurs de R³. Donner la matrice de cette application linéaire.
2. Réciproquement, pour visualiser un objet en 3D sur l'écran (qui n'a que deux dimensions), il faut faire une projection de R³ dans R². Nous supposerons que l'observateur regarde depuis le haut, de sorte que la projection se fera sur le plan des x et y. Donner la matrice de cette application linéaire.
3. Calculer le produit des deux matrices correspondant au plongement de R² dans R³ suivi de la projection de R³ dans R². Interprétation?
4. Afficher le polygone après plongement puis projection.
5. Donner la matrice de la rotation de R³ d'angle θ autour de l'axe des x. Indication: faire un dessin, et chercher l'image des vecteurs de la base canonique. Afficher le polygone après plongement, rotation de 45 degrés puis projection. Animer le résultat pour θ variant de 0 à 359 degrés.

Exercice 10   Probablement trop ambitieux.

Exercice 11   Soit f := x ↦ sin(x). Tracer son graphe avec

    f := sin:
    plot(plot::Function2d(f))
  

Notre objectif est de construire des fonctions simples qui approximent f aux alentours d'un point x₀.

1. Chercher une constante a₀ telle que la fonction constante g := a₀ approxime au mieux f aux environs de 0. Tracer son graphe par dessus celui de f avec

   
         plot(plot::Function2d(g(x)), plot::Function2d(g(x)))
       

   Zoomer le graphique.
2. Chercher une fonction affine g := a₀ + a₁ x qui approxime au mieux f aux environs de x₀:=0. La comparer graphiquement avec f.
3. Chercher une fonction affine g := a₀ + a₁ (x−x₀) qui approxime au mieux f aux environs de x₀ := π/4 (π se note PI).

4. 
         xmin := -2*PI:
         xmax := 2*PI:
         plot(plot::Function2d(sin(x), x=xmin..xmax),
              plot::Function2d(f(x0) + f'(x0)*(x-x0), x=xmin..xmax, x0=xmin..xmax),
              ViewingBoxYRange=-2..2)
      

Exercice 12  

Exercice 13   Un vieux pirate est sur son lit de mort. Dans sa jeunesse il a enfoui un Fabuleux Trésor dans la lagune interminable de l'Ile de la Tortue, quelque part à l'est du Grand Cocotier. Il a réuni ses dix lieutenants préférés pour leur transmettre l'information secrète indispensable: la distance entre le Grand Cocotier et le Trésor. Connaissant bien ses lieutenants, et dans un étonnant dernier sursaut de justice, il ne voudrait pas qu'une conjuration de quelques uns d'entre eux assassines les autres pour empocher seuls le trésor. En tenant cependant compte de la mortalité habituelle du milieu, il souhaite donner une information secrète à chacun de ses lieutenants pour que sept survivants puissent toujours retrouver ensemble le trésor, mais pas moins. Comment peut-il s'y prendre?

1. « The art of doing mathematics consists in finding that special case which contains all the germs of generality » – David Hilbert
   
   Autrement dit, la première chose à faire pour attaquer ce genre de problème est de le généraliser pour des paramètres quelconques, et de commencer par essayer de comprendre ce qu'il se passe pour de petites valeurs des paramètres. Ici, les paramètres naturels sont le nombre n de lieutenants, et le nombre k de survivants. Que peut on dire pour n≤ 1? pour k≤ 1?
2. Étudions maintenant le cas n=k=2. Soit b la distance secrète. Le pirate choisit au hasard un coefficient a qu'il garde secret, et considère la fonction f(x) = ax+b. Puis il choisit au hasard deux points d'évaluation x₁:=−3 et x₂:=7 qu'il annonce publiquement. Enfin, il dit en secret au premier pirate que f(x₁) = 5 et au deuxième pirate que f(x₂) = 7. Les deux pirates se mettent ensemble; retrouver la valeur de b. Est-ce que le premier pirate aurait pu la retrouver tout seul?
3. Généralisation pour n=10 et k=7: choisir une valeur secrète b. Tirer au hasard les coefficients d'un polynôme f(x) = a₆ x⁶ +...+a₁ x + b de degré 6 et dont le terme constant est b. Tirer au hasard dix points d'évaluation x₁,...,x₁0 distincts et non nuls, et calculer f(x₁),...,f(x₁0). À l'aide de la commande interpolate, et en utilisant uniquement x₁,...,x₇ et f(x₁),...,f(x₇) retrouver la valeur de b. Pour se mettre en condition réelle, donner à chaque étudiant du TP un couple (x_i, f(x_i)), et laissez les retrouver ensemble la valeur secrète.