Étude de l’algorithme de Kruskal

Dans ce qui suit nous exécutons pas à pas, l’algorithme de Kruskal :

from graph import Graph, examples
import networkx
import matplotlib
import matplotlib.pyplot as plt

## On part d'un graphe valué et on fixe un dessin
G = examples.cours_1_reseau()
GNX = G.networkx()
layout = networkx.planar_layout(GNX)
edges_weight = {(u, v) : w for u, v, w in G.edges()}

## On visualise la progression de l'algorithme en affectant à chaque arête un état représenté par une couleur

from enum import Enum, unique
@unique
class Status(Enum):
    AFAIRE = 0
    GARDEE = 1
    SUPRIMEE = 2
    ENCOURS = 3
colors_code = { 
    Status.AFAIRE : 'black',
    Status.GARDEE : 'green',
    Status.SUPRIMEE : 'lightgray',
    Status.ENCOURS : 'red'
}

def show_kruskal(status):
    plt.figure()
    colors = [colors_code[status[u,v]] for (u, v) in GNX.edges()]
    networkx.draw(GNX, layout, edge_color = colors, width=3, linewidths=1,
                  node_size=500, node_color = 'lightgray', alpha=0.9,
                  labels = {node : node for node in G.nodes()})
    networkx.draw_networkx_edge_labels(GNX, layout, edge_labels= edges_weight, font_color='black')
    plt.axis('off')
    plt.show()

# Au début toutes les arêtes sont marquée "à faire"
edges_status = {(u, v) : Status.AFAIRE for u, v, _ in G.edges()}
show_kruskal(edges_status)

# On choisit l'une des arêtes de poids minimum
edges_status["F", "G"] = Status.ENCOURS
show_kruskal(edges_status)

# Elle ne crée pas de cycle. On la garde
edges_status["F", "G"] = Status.GARDEE
show_kruskal(edges_status)

# On choisit l'une des arêtes de poids minimum
edges_status["B", "C"] = Status.ENCOURS
show_kruskal(edges_status)

# Elle ne crée pas de cycle. On la garde
edges_status["B", "C"] = Status.GARDEE
show_kruskal(edges_status)

# L'algorithme se continue ainsi
edges_status["B", "G"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["B", "G"] = Status.GARDEE
edges_status["A", "G"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["A", "G"] = Status.GARDEE
edges_status["C", "H"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["C", "H"] = Status.GARDEE
edges_status["E", "G"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["E", "G"] = Status.GARDEE
show_kruskal(edges_status)

# On Passe maintenant aux arêtes de poids 3
edges_status["E", "F"] = Status.ENCOURS
show_kruskal(edges_status)

# L'arête E - F crée un Cycle, on la supprime
edges_status["E", "F"] = Status.SUPRIMEE
show_kruskal(edges_status)

# On Passe maintenant a A - B
edges_status["A", "B"] = Status.ENCOURS
show_kruskal(edges_status)

# L'arête A - B crée un Cycle, on la supprime
edges_status["A", "B"] = Status.SUPRIMEE
show_kruskal(edges_status)

# Idem pour E - H
edges_status["E", "H"] = Status.SUPRIMEE
show_kruskal(edges_status)

# L'algorithme se poursuit
edges_status["A", "F"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["A", "F"] = Status.SUPRIMEE
edges_status["C", "D"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["C", "D"] = Status.GARDEE
edges_status["G", "H"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["G", "H"] = Status.SUPRIMEE
show_kruskal(edges_status)

# On pourrait continuer jusqu'à ce que l'on ai vu toutes les arêtes...
# On remarque que l'on a choisi 7 arêtes dans un graphe à 8 sommets. On peut donc s'arrêter dès maintenant.
edges_status["C", "G"] = Status.SUPRIMEE
edges_status["D", "E"] = Status.SUPRIMEE
edges_status["D", "H"] = Status.SUPRIMEE
show_kruskal(edges_status)

On a calculé un arbre couvrant de poids 13 du graphe.

L’invariant de l’algorithme est le suivant:

À chaque étape, le graphe des arêtes choisies est un graphe partiel acyclique de \(G\) de poids minimum

Exercice

1. Appliquez à la main l’algorithme de Kruskal aux deux graphes suivants. On donnera un arbre couvrant de poids minimal et un arbre couvrant de poids maximal. Pour ce dernier on applique le même algorithme mais en choissant un arête de plus fort poids. Donnez le poids de l’arbre couvrant obtenu.

   

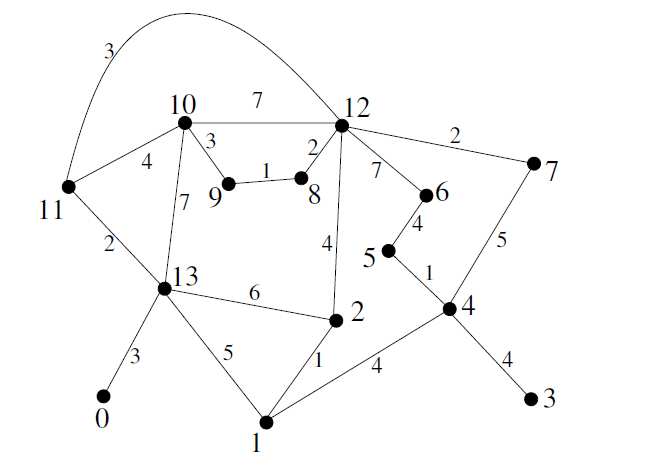
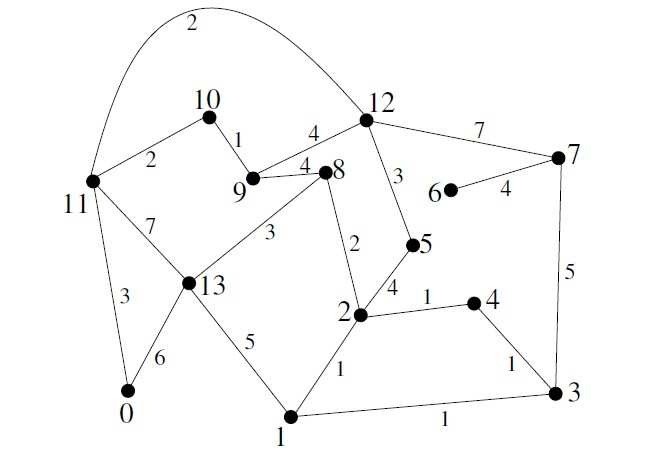
2. Expliquez pourquoi l’invariant est conservé.