Previous: Homework assignment 12Homework assignment 12 Up: Homework assignmentsHomework assignments
Document also available in PDF, Postscript, DVI, pure text and LaTeX.

Homework assignment 13



4.4. Functions

Exercise 1  [23 p. 304]   Let f:S-> T and g:T-> U be functions.
  1. Prove that if go f is one-to-one, so is f.
  2. Prove that if go f is onto, so is g.
  3. Find an example where go f is one-to-one but g is not one-to-one.
  4. Find an example where go f is onto but f is not onto.
Proof: [Correction]
  1. Let's assume go f is one-to-one, and take x and y two elements of S such that f(x)=f(y). In order to prove that f is one to one, we just need to check that x=y. Clearly, by using the assumption, g(f(x))=g(f(y)), i. e. go f(x)=go f(y). Now, since go f is one-to-one, we indeed have x=y, which concludes the proof.
  2. Let's assume that go f is onto, and take z in the codomain U of g. Then, there is an element x in S such that go f(x)=z. Take y:=f(x); this is an element of T, and we have g(y)=z, so z has a preimage by g. Conclusion: g is onto.
Exercise 2  [29 p. 305]   Let A be any set and let SA be the set of all permutations of A. Let f, g, h in SA. Prove that the functions ho (go f) and (ho g)o f are equal, thereby showing that we can write ho g o f without parentheses to indicate grouping.
Proof: [Correction] The functions ho (go f) and (ho g)o f have same domain and codomain. It remains to check that they give the same value to any element of the domain: given an element x of the domain, we have:
(fo g)o h(x) = (fo g)(h(x)) = f(g(h(x)))
  = f((go h)(x)) = fo(go h)(x).
Conclusion: those two functions are indeed equal.

Exercise 3  [31a p. 305]   Find the composition of the following cycles representing permutations on N. Write your answer as a composition of one or more disjoint cycles.
  1. (3,5,2)o(6,2,4,1)o(4,8,6,2)
Proof: [Correction] (3,5,2)o(6,2,4,1)o(4,8,6,2)=(
1 2 3 4 5 6 7 8
6 1 5 8 2 4 7 3
)=(6, 4, 8, 3, 5, 2, 1)

Exercise 4  [32 p. 305]   Find a permutation on an infinite set that can't be written as a cycle.
Proof: [Correction] Just take Z as infinite set, and the function f: x|-> x+1. Obviously, f is a permutation. However, if we try to build a cycle, as we did for permutations of finite sets, the process is never going to stop. For example, if we start at 1, we get a cycle that starts as follow (1,2,3,4,5,...), but never cycles back to 1.

Exercise 5  [33 p. 305]   The ``pushdown store,'' or ``stack,'' is a storage structure operating much like a set of plates stacked on a spring in a cafeteria. All storage locations are initially empty. An item of data is added to the top of the stack by a ``push'' instruction, which pushes any previous stored items further down in the stack. Only the top-most item on the stack is accessible at any moment, and it is fetched and removed from the stack by a ``pop'' instruction.

Let's consider strings of integers that are an even number of characters in length; half the characters are positive integers, and the other half are zeros. We process these strings through a pushdown store as follows: As we read from left to right, the push instruction is applied to any nonzero integer, and a zero causes the pop instruction to be applied to the stack, thus printing the popped integer. Thus processing the string 12030040 results in an output of 2314, and processing 12304000 results in an output of 3421. A string such as 10020340 cannot be handled by this procedure, because we cannot pop two integers from a stack containing only one integer. Both 2314 and 3421 can be thought of as permutations,
(
(
1 2 3 4
2 3 1 4
)
)		 and (
(
1 2 3 4
3 4 2 1
)
)
respectively, on the set A={1,2,3,4}.
  1. What permutation of A={1,2,3,4} is generated by applying the procedure to the string 12003400?
  2. Name a permutation of A={1,2,3,4} that cannot be generated from any string where the digits 1, 2, 3, and 4 appear in order, no matter where the zeros are placed.
Proof: [Correction]
  1. 2134.
  2. 4123. Indeed, if the first integer which is popped out is 4, then there is no 0 in the string before 4. But then, the string is 12340000, and the resulting permutation should be 4321 instead.
Exercise 6   Draw all binary trees on 1,2,3 and 4 nodes. What conjecture does it suggest to you ? Use recursion to prove it.
Proof: [Correction] We obtain respectively 1, 2, 5 and 14 binary trees. This is the same sequence for binary trees, and suggests the following conjecture: the number of binary trees on n nodes is equal to the number of ordered trees on n nodes.

Let's prove this conjecture. For practical reason, we are actually going to build by induction a bijection f between ordered trees on n nodes and binary trees on n nodes where the topmost node has no right child. Those in turn are in bijection with binary trees with n-1 nodes, by simply pruning the topmost node.

Construction of f:

Base case: n=1: the image of a single node by f is a single node.

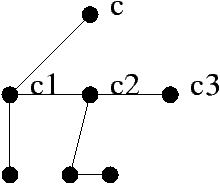
Induction step: let t be an ordered tree on n>1 nodes. Let c be the top node of t, c1,...,ck its children, and t1,···,tk be the subtrees pending from those children. The images of those subtrees by f are binary trees with the same number of nodes, and with no right child. Now f(t) is constructed as follow: c has no right child. The left child of c is c1, and we attach f(t1) here. The right child of c1 is c2, with f(t2) attached. The right child of c2 is c3 with f(t3) attached. And so on, and so forth.

To summarize, each node points to two over nodes: on the left its first child in t if it has one, and on the right its next brother in t if it has one. Below are drawn an ordered tree (on the left) and its image by f (on the right). To make the correspondence more obvious, the nodes of the binary tree has been drawn at the same positions at the corresponding nodes in the ordered tree. Links from a node to its left child are non-horizontal, whereas links from a node to its right child are horizontal.
    

This process could be inverted (check this by providing an algorithm!), and so f is indeed a bijection.
Previous: Homework assignment 12Homework assignment 12 Up: Homework assignmentsHomework assignments
Homework assignment 13 / CSM MACS-358 / Nicolas M. Thiéry
Last modified: Tue Dec 2 13:40:44 2003