 Proof Of Correctness
Proof Of Correctness
 Class notes
Class notes
 Sets
Sets
Document also available in PDF, Postscript, DVI, Text, LaTeX, LyX.
Chapter 1 Analysis of Algorithm (Section 2.5)
Exemple 1
Finding an element in a list.
Computing the nth Fibonacci number F(n).
Problem 1
How long will my program take to execute ?
How much memory do I need ?
How efficient is my algorithm ?
Is it the best one ?
Which algorithm should I choose ?
Goal: "measure" the quality of an algorithm:
-
Time
- Memory
- Easiness of writing
1.1 Complexity of an algorithm: Measuring time
Définition 1
Decide which operations are basic (i.e. multiplications).
Complexity of the algorithm: how many basic operations are
needed.
Exemple 2
Sequential search
-
SequentialSearch(x,l)
// Preconditions:
// - l is a list ["bonjour","car","hello","juggler"]
// - x is a string
// Postcondition: return true iff x is in the list
Begin
// compare successively x with l[1], l[2], ..., l[n]
For i From 1 To n Do
If (x=l[i]) Then Return TRUE; EndIf
EndFor;
Return FALSE;
End;
How many operations ?
-
x = "unicycle":
- x = "juggler":
- x = "hello":
- x = "car":
Worst case: n basic operations
Average case: depends on the probability for x to be in the list.
Difficult !
Résumé 1
n: size of the data (here, the length of the list)
Worst case: maximum number of operations for a data of size n.
Average case: average number of operations for a data of size n
(difficult)
Exemple 3
Binary search
A non sorted dictionary is useless!!!
-
BinarySearch(x, l)
// Preconditions:
// - l is sorted ["bonjour","car","hello","juggler"]
// - x is a string
// Postcondition: return true iff x is in the list
Begin
If n=1 Then
Return x=l[1];
ElseIf x <= l[n/2] Then
Return BinarySearch(x, [l[1], ..., l[n/2]]);
Else
Return BinarySearch(x, [l[n/2]+1, ..., l[n]]);
End if
End
How many operations ?
For n, there is at most k operations, where k is the smallest
integer such that 2k-1>= n.
log(n): logarithm of n other base 2
Number of operations: log(n)
1.1.1 How precise ?
The estimate above does not give a precise measure of the time needed.
It depends in particular on:
-
What computer you are using
- How long are the strings
- The computer language:
-
How fast are strings
- How fast are for loops
- How fast are function calls
A precise measure of the time is often hard to obtain.
Most of the time, to decide between to algorithms, a rough order of
magnitude is enough.
Draw the graphs to get an idea if there are big differences
-
4n operations / 7n operations?
- 4n operations / 7n operations ?
- n operations / n+3 operations ?
- log(n) operations / n operations ?
- n operations / n2 operations ?
- n operations / exp(n) operations ?
Définition 2
An algorithm is of complexity O(n5) if it needs less than Cn5+K
operations to execute, where C and K are some constant.
-
O(1): constant (random access to an element of an array)
- O(log(n)) : logarithmic (random access in a sorted list
by binary search)
- O(n): linear (random access in a linked list; sequential search)
- O(nlog(n)): (sorting a list by a good algorithm)
- O(n2): quadratic (sorting a list by bubble sort)
- O(nk): polynomial
- O(exp(n)): exponential
Worst case analysis is usually easier. It is important if your need
a warranty on the time needed for each data (e.g.: real time data
acquisition).
Average case analysis is more difficult. It is important when running
over a large sample of data.
1.1.2 Case study: the Fibonacci sequence
Here is a program written in MuPAD www.mupad.de (free Computer
Algebra system).
It present different implementations of the computation of the Fibonacci
sequence.
-
/*
fibonacci_rec (n: Dom::Integer);
fibonacci_rec_remember (n: Dom::Integer);
fibonacci_loop_array (n: Dom::Integer);
fibonacci_loop (n: Dom::Integer);
Precondition: n non negative integer
Postcondition: returns the nth fibonacci number
Also increments the global variable operations.
*/
fibonacci_rec:=
proc(n: Dom::Integer)
begin
if n=0 then return(1); end_if;
if n=1 then return(1); end_if;
operations:=operations+1; // Count operations
return(fibonacci_rec(n-1)+fibonacci_rec(n-2));
end_proc:
fibonacci_array:=
proc(n:Dom::Integer)
local i, F;
begin
if n=0 then return(0); end_if;
if n=1 then return(1); end_if;
F[0]:=0;
F[1]:=1;
for i from 2 to n do
operations := operations+1; // Count operations
F[i] := F[i-1] + F[i-2];
end_for;
return(tableau(n));
end_proc:
fibonacci_loop:=
proc(n:Dom::Integer)
option remember;
local i, value, previous, previousprevious;
begin
if n=0 then return(0); end_if;
if n=1 then return(1); end_if;
previous:=0;
value:=1;
for i from 2 to n do
operations := operations+1; // Count operations
previousprevious:= previous;
previous := value;
value := previousprevious+previous;
end_for;
return(value);
end_proc:
fibonacci_rec_remember:=
proc(n: Dom::Integer)
option remember;
begin
if n=0 then return(0); end_if;
if n=1 then return(1); end_if;
operations := operations+1; // Count operations
return(fibonacci_rec_remember(n-1)+
fibonacci_rec_remember(n-2) );
end_proc:
printentry:=
proc(x)
begin
userinfo(0, NoNL, x);
userinfo(0, NoNL, "t");
end_proc:
for n from 0 to 30 do
printentry(n);
operations:=0;
printentry(fibonacci_rec(n));
printentry(operations);
operations:=0;
fibonacci_array(n);
printentry(operations);
operations:=0;
fibonacci_loop(n);
printentry(operations);
operations:=0;
fibonacci_rec_remember(n);
printentry(operations);
// Clear remember table;
fibonacci_rec_remember:=
subsop(fibonacci_rec_remember,5=NIL);
print();
end_for:
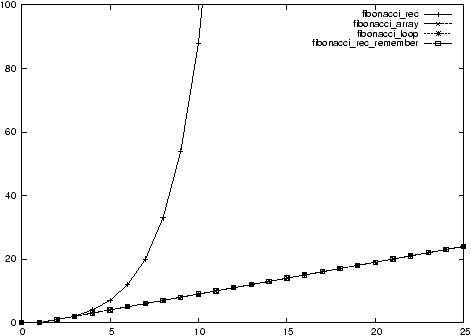
Figure 1.1: Measurement of the complexity of the different implementations of
the Fibonacci sequence
Problem 2
Why is Fibonacci rec so slow ? (Trace its execution)
How to avoid this?
Don't throw away the results !
The remember option.
Time consumption:
-
Fibonacci rec: exponential
- Fibonacci rec_remember: linear
- Fibonacci array: linear
- Fibonacci loop: linear
Memory consumption:
-
Fibonacci rec: exponential
- Fibonacci rec_remember: linear
- Fibonacci array: linear
- Fibonacci loop: constant
Easiness to write:
-
Fibonacci rec: straight forward
- Fibonacci rec_remember: straight forward
- Fibonacci array: easy
- Fibonacci loop: harder
1.2 The P=NP conjecture
1.2.1 Case study: Satisfying a well formed formula of propositional logic
We consider a well formed formulas of propositional logic.
Définition 3
A choice of truth values for A, B, C, ... satisfies
P if P evaluates to true.
Exemple 4
A true and B true satisfies A/\ B.
A true and B false do not satisfy A/\ B.
Problem 1
Given the truth values of A, B, C, ... check if they satisfy
P.
Algorithm ?
Complexity ?
Définition 4
A wff P is satisfiable if at least one choice of truth values
for A, B, C, ... satisfies P.
I.e. P is not a contradiction.
Exemple 5
A/\ B is satisfiable, whereas A/\ A' is not.
Problem 2
Testing if a wff P is satisfiable.
Algorithm ?
Complexity ?
Is this the best algorithm ?
Does there exist a polynomial algorithm ?
That's an instance of a problem where:
-
checking a solution is easy (polynomial)
- finding the solution seems to be hard (the best known algorithm is
exponential)
Exemple 6
Checking if the solution of a crossword puzzle is correct is easy.
Solving the crossword puzzle is not !
Exemple 7
Backpack problem with size=23, and objects=5,7,7,20,17,5,11,5,19,14.
1.2.2 Polynomial and Non Deterministic Polynomial problems
Définition 5
Problems as above are called NP (Non-deterministic Polynomial)
P: collection of all polynomial problems
NP: collection of all NP problems
Problem 3
P = NP ?
In other words:
If it's easy to check a potential solution of a problem,
is there necessarily an easy way to find the solution ?
Intuitively, no. This cannot be true.
Well, despite a lot of research, we still have no proof!
This is the main problem of theoretical computer science since 30
years.
So, this is YOUR job to find the solution !

 Proof Of Correctness
Proof Of Correctness
 Class notes
Class notes
 Sets
Sets
Analysis Of Algorithms /
CSM MACS-358 /
Nicolas M. Thiéry
Last modified: Fri Jan 19 13:12:15 2007