Combinatorics
Combinatorics
 Class notes
Class notes
 Functions
Functions
Document also available in PDF, Postscript, DVI, Text, LaTeX, LyX.
Chapter 1 Relations (section 4.1, 4.2 and 4.4)
1.1 Introduction
A mere set of words would not make a good dictionary.
It would be a pain to find a particular word!
A usable dictionary has some structure: the words are sorted.
In general, the more structure a set have, the more useful
it is.
A way to bring structure into this set is to describe the relations
between its elements, or between its elements and the elements of
another set.
In this section we will see how we can formalize and study relations.
Exemple 1
Imagine you want to build a house.
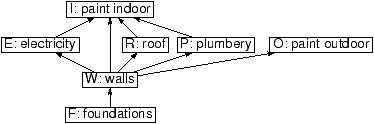
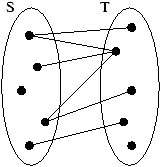
Figure 1.1 shows the tasks that need to be completed.
Figure 1.1: Tasks to build a house
Let S:={ F,W,E,I,O,R} be the set of all tasks.
Problem: can we do the tasks in any order ?
For example, it would be better to build the walls AFTER the foundations!
S in itself does not contain enough information to choose a correct
order.
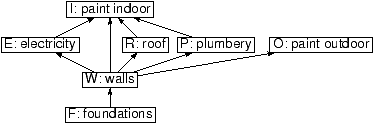
Figure 1.2: Constraints between the tasks to build a house
Set of constraints: rho:={(F,W),(W,O),(W,E),(R,E),(R,I)}.
This set of constraints gives some structure to S, and makes it
useful.
1.2 Relations
1.2.1 Definitions
Définition 1
A binary relation on a set S is a subset rho of S× S.
Let x and y be two elements of S.
Then x is in relation with y (denoted x rho y)
iff (x,y)inrho.
Exemple 2
Let rho be the relation ``is a prerequisite for'':
rho:={(F,W),(W,O),(W,E),(R,E),(R,I)}
Then, (F,W)inrho, but (I,O)not inrho.
So, F rho W is true, whereas I rho O
is false.
A relation can be defined by a property.
Exercice 1
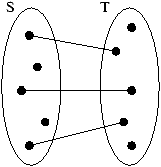
Let S:={1,2,3,4,5}. Draw the relations defined by:
-
x rho1 y iff x=y;
- x rho2 y iff x<= y;
- x rho3 y iff x divides y;
- x rho4 y iff x-y is even.
Définition 2
A binary relation between two sets S and T is a subset
rho of S× T.
A n-ary relation between n sets S1,...,Sn is
a subset rho of S1×···× Sn.
Exemple 3
Let M be a set of male and F a set of female students.
We can define the relation ``is married to''.
1.2.2 Basic properties of relations
Is there anything particular about the relation ``is married to''
?
Définition 3
Let rho be a relation between S and T.
-
S is one-to-one if any element of S and T appears
at most once in rho;
-
S is one-to-many if any element of T appears at most
once in rho;
-
S is many-to-one if any element of S appears at most
once in rho;
-
S is many-to-many in all other cases.
Exemple 4
Is x lower or equal to itself ?
Définition 4
A relation rho on a set S is reflexive
iff
(for all xin S) x rho x.
Exemple 5
Assume x is equal to y. Is y equal to x ?
Définition 5
A relation rho on a set S is symmetric
iff
(for all xin S)(for all yin S) (x rho y)<->(y rho x).
Exemple 6
Assume x<= y and y<= x. What can you say about x and
y?
Définition 6
A relation rho on a set S is antisymmetric
iff
(for all xin S)(for all yin S)[(x rho y) and (y rho x)]->(x=y).
Exemple 7
Assume x<y and y<z. What can you say about x and z?
Définition 7
A relation rho on a set S is transitive
iff
(for all xin S)(for all yin S)(for all zin S)[(x rho y) and (y rho z)]->(x rho z).
Exemple 8
What are the properties of the following relations
-
<, <=, =;
- ``is married to'';
- ``is a friend of'';
- ``has the same color than''.
1.2.3 Operations on relations
A relation is basically a set. So, we can use all usual set operations
on relations.
Remarque 1
Let S and T be two sets.
The powerset (S× T) is the set of all binary relations
between S and T.
Définition 8
Let rho and sigma be two relations between S and T.
We can construct the following new relations:
-
union: rhounionsigma,
- intersection: rhointersectsigma,
- complement: rho',
- ...
Exemple 9
Let S:=N.
-
What is the union of <and =?
- What is the intersection of < and >?
- What is the union of < and >?
- Is <a sub relation of <= ?
1.2.4 Closure of a relation
Exemple 10
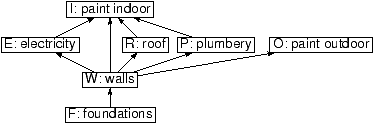
Lets come back to the example of the house building.
Figure 1.1: Constraints between the tasks to build a
house
Do you have to do the electricity after the foundations ?
Foundations is not a direct prerequisite for electricity.
However, it still needs to be done before electricity.
The relation ``has to be done before'' is transitive, and contains
the relation
``is a prerequisite for''. It's the transitive closure
of ``is a prerequisite for''.
Définition 9
Let rho be a relation.
The transitive closure of rho is the smallest transitive
relation rho*containing rho.
Exercice 2
Draw the transitive closure of ``is a prerequisite for''.
Problem 1
Is there an algorithm for computing the transivite relation of a relation?
Algorithme 2
Construction of the transitive closure rho*.
-
rho*:=rho;
- Find x, y, z such that (x rho*y), (y rho*z),
and (x ¬ rho*z);
- If no such triple exists, rho*is transitive; Exit;
- rho*:=rho*union{(x,z)};
- Repeat at step 2.
Remarque 2
The order in which you add the pairs to rho is irrelevant.
Exemple 11
Draw the relation ``has to be done before'' (Figure 1.1).
Définition 10
Let rho be a relation.
The reflexive closure of rho is the smallest reflexive
relation containing rho.
The symmetric closure of rho is the smallest symmetric
relation containing rho.
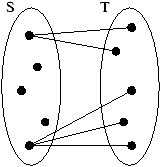
Exercice 3
Consider the following relation:
-
Draw its reflexive closure
- Draw its symmetric closure
- Draw its transitive closure
- Draw its antisymmetric closure
Remarque 3
The antisymmetric closure of a relation cannot be uniquely defined!
1.3 Equivalence relations
Exemple 12
Consider a set of cars, and the relation ``has the same color as''.
What are the properties of this relation?
Définition 11
An equivalence relation
is a relation which is
-
Reflexive
- Symmetric
- Transitive
Définition 12
Let rho be a relation on a set S, and x be an element of
S.
The equivalence class of x is the set [x]of all elements
y such that x rho y.
Exemple 13
The equivalence class of a car is the set of all cars having same
color.
Remarque 4
If x rho y, then [x]=[y].
Exemple 14
Consider the relation same as3 on N defined by xsame as3y
iff 3 divides x-y.
(we also say that x and y are congruent modulo 3:
xsame as y (mod 3))
What are the equivalence classes?
Définition 13
A partition of a set S is a collection of subsets { A1,...,Ak}
of S such that:
-
A1union···union Ak=S
- Aiintersect Aj=Ø for any i, j.
Exemple 15
Consider a set S of car, whose color are either red, blue, or green.
Define the following subsets of S:
R (red cars), B (blue cars), and G (green cars) .
Then, { R,B,G} is a partition of S.
The equivalence relation ``has the same color'' and the partition
of the cars by color are closely related.
Théorème 1
In general:
-
An equivalence relation on S defines a unique partition of S.
- A partition of S defines a unique equivalence relation on S.
Proof.
Left as exercise:
-
Construct the collection { A1,...,Ak}, and prove it
is indeed a partition of S.
- Construct the relation rho, and prove it's indeed an equivalence
relation.
Définition 14
Let S be a set, and rho be a relation on S.
The set of all the equivalence classes is called the quotient
of S by rho.
Remarque 5
This method is used a lot in set theory:
Construction of Z from N.
Construction of Z/nZ (integers modulo n) from Z.
Construction of Q from Z.
1.4 Partially Ordered Sets
Exemple 16
What are the properties of the relation ``has to be done before''
on the tasks to build a house ?
Définition 15
A partially ordered set
(or poset
) is a set S with
a relation rho which is
-
Reflexive
- Antisymmetric
- Transitive
Exemple 17
Which of the following are posets ?
-
({1,2,3,4},<=);
- ({1,2,3,4},<);
- ({1,2,3,4},=);
- ({1,2,3,4},rho), with x rho y iff x
divides y.
- (({1,2,3,4}),included in or equal to).
1.4.1 Drawing posets; Hasse diagrams
Définition 16
Some names:
-
Node (or vertex)
- Predecessor
- Immediate predecessor
- Maximal element
- Minimal element
- Least element
- Greatest element
Définition 17
The Hasse diagram
of a poset is a drawing of this poset such
that:
-
If x rho y, then y is higher than x;
- The loops are not drawn;
- There is a segment linking x and y iff x is an immediate
predecessor of y.
Exemple 18
Draw all posets on 1, 2, 3, 4 indistinct nodes.
How many such posets are there on 10 nodes ?
1.4.2 Scheduling
Scheduling a set of tasks consist in allocating tasks to resources,
subject to certain constraints.
Exemple 19
Consider the house building problem, with the following assumptions:
-
All tasks take the one day to complete;
- One worker can only work on one task every day;
- It does not save time to have two workers working on the same task.
Figure 1.1: Constraints between the tasks to build a
house
Schedule the tasks between 2 workers to optimize the completion time:
| |
Day 1 |
Day 2 |
Day 3 |
Day 4 |
Day 5 |
Day 6 |
Day 7 |
| Worker 1 |
|
|
|
|
|
|
|
| Worker 2 |
|
|
|
|
|
|
|
What if there is one worker ?
| |
Day 1 |
Day 2 |
Day 3 |
Day 4 |
Day 5 |
Day 6 |
Day 7 |
| Worker 1 |
|
|
|
|
|
|
|
What if there are three workers ?
| |
Day 1 |
Day 2 |
Day 3 |
Day 4 |
Day 5 |
Day 6 |
Day7 |
| Worker 1 |
|
|
|
|
|
|
|
| Worker 2 |
|
|
|
|
|
|
|
| Worker 3 |
|
|
|
|
|
|
|
Proposition 1
Consider the problem of scheduling n tasks on p processors, subject
to precedence constraints, with the same assumptions and goal as above.
-
1 or 2 processors: algorithms in O(n2);
- 3 processors: complexity unknown;
- p processors: NP-complete
(basically the only known algorithm is exhaustive search);
- oo processors: O(n).
This is typical from scheduling problems, where a very small change
in the constraints can make huge differences in the complexity of
the problems.
Also, usually the complexity is as follow:
-
No constraints: low complexity;
- Some constraints: higher and higher complexity;
- More constraints: NP-complete. The only known algorithm is exhaustive
search through all plausible cases (branch-and-cut);
- Even more constraints: still NP-complete, but easier. Indeed more
and more cases can be thrown away very early.
Having very good scheduling algorithms is vital in industry, because
a 1% difference in completion time (for example) can save thousands
of dollars. Consequently, research in this topic is well financed!
1.5 Conclusion
-
The more structure a set has, the more useful it is.
- Defining a relation is a way to add structure to a set.
- Relations, posets, equivalence relations, ... are just abstract
models of natural notions commonly used in real life.

 Combinatorics
Combinatorics
 Class notes
Class notes
 Functions
Functions
Relations /
CSM MACS-358 /
Nicolas M. Thiéry
Last modified: Fri Jan 19 13:12:20 2007