Up: Class notesClass notes Next: IntroductionIntroduction
Document also available in PDF, Postscript, DVI, Text, LaTeX, LyX.

Algebraic Structures



nthiery@users.sf.net mailto:nthiery@users.sf.net

http://www.lapcs.univ-lyon1.fr/~nthiery/

LaPCS, Université Claude Bernard Lyon I, Bâtiment recherche [B]
50, avenue Tony-Garnier, Domaine de Gerland,
69366 Lyon Cedex 07, FRANCE

1

1
Those notes grew up from the class MACS 358 that I taught during three semesters at the Colorado School of Mines, using the textbook Mathematical Structures for Computer Sciences (4th edition) by Judith L. Gersting[1].
Copyright Nicolas M. Thiéry 1999-2000
They are released, with the approbation of the publisher of the textbook, under the GNU Free Documentation License (see http://www.gnu.org/copyleft/fdl.html): in short, copying, redistribution in any form, modification or reuse is permitted, and even encouraged, as long as I get credit for the original version, and don't get blamed for other's modifications. Moreover, any suggestions for improvements are warmly welcomed.
I use LyX http://www.lyx.org to typeset them, as well as to display them in class on a LCD-projector plugged in my laptop. The dvi, PDF, ps, HTML and pure text versions are then created using LATEX, Hevea http://para.inria.fr/~maranget/hevea/, Htmlpp http://htmlpp.sourceforge.net, and some Makefile magic. I highly recommend the PDF of ps versions, since the HTML and pure text versions are far from perfect due to the limitations of those formats.

Table of Contents

Chapter 1  Introduction

1.1  Course Objectives

Mathematical tools for solving problems arising from computer science.

Using a computer to solve problems.

1.2  Pólya's hints for solving a problem

There are two main kinds of problems:
  1. Problems to solve
  2. Problems to prove
Here is a list of general questions that will guide you when you try to solve a problem.

Most of them are borrowed from ``How to solve it'' by Pólya[3, p. XVI].

(*subliminal hint* you definitely should read this book!)

Whenever you get stuck and don't know what to do, browse through them, and most likely one of them will give you something to try out.

1.2.1  Phase 1: Understanding the problem

You have to understand the problem.
  1. What is the goal ?
  2. What is the condition ?
  3. Look at examples. Draw a figure. Introduce suitable notations.
  4. How would you store the data on a computer ?

1.2.2  Phase 2: Devising a plan

Find the connection between the data and the unknown.

You may be obliged to consider auxiliary problems if an immediate connection cannot be found.

You should obtain eventually a plan of the solution.
  1. Have you seen it before?
  2. Here is a problem related to yours and solved before. Could you use it?
  3. Could you restate the problem? Could you restate it still differently?
  4. Go back to definitions.
  5. If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem? A more general problem? A more special problem? An analogous problem?
  6. Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problems?

1.2.3  Phase 3: Carrying out the plan

Carry out your plan.
  1. Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove it is correct?

1.2.4  Phase 4: Looking back

Examine the solution obtained.
  1. Can you check the result? Can you check the argument?
  2. Can you derive the result differently? Can you see it at a glance?
  3. What's the structure behind?
  4. Can you use the result, or the method for some other problem?
  5. Can you make it an algorithm ?

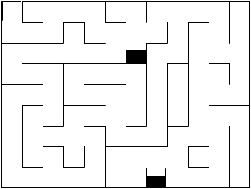
1.3  Some ``research'' about Mazes





1.4  Conclusion

The purpose of this exercise was to browse quickly through what we are going to do this semester:

1.4.1  General problem solving techniques:

We have used Pólya's list of questions as a guide to solve our problems. We will do this over and over. Usually the main difficulty with a problem is to get started. Whenever you get stuck on a problem, and don't know what to do, you should refer to this list, and see if some of the questions could give you something to try out.

1.4.2  Proofs

At some time, we had a solution for exiting from a maze. However, we were not sure if it worked all the time or not. Well, the only way to be sure that something is correct is to PROVE it.

We will need to learn how to prove things before anything else. In particular we will want to prove that certain algorithms are correct. That will be the core of our first month of class.

So what's a proof ? Basically, it's a message written by a human A to convince another human B that some fact is true (possibly A and B are the same person). When B reads through the message, he should not have any choice at the end but to say "I agree". To achieve this goal, our primary tool will be Formal Logic.

It's not easy to write good proofs. For example, a proof should be short enough that you don't get lost in the details, and detailed enough that you are sure not to have left a hole somewhere. Learning to write proofs is like learning to write. The only way is to write a lot of proofs yourself, and to take model on other's proofs. We will learn this progressively.

1.4.3  Discrete structures:

We have seen that the very structure of a maze (once we have removed all extraneous information like color, shape and so on) can be formalized with a graph, that is a set of nodes which are connected or not by edges.

A graph is a good example of discrete object, or structure (in opposition to a continuous object like a curve). We are going to see other discrete structures, and learn to recognize them when the arise at the very heart of problems. We are also going to see how to deal with such structures (algorithms and such).

1.4.4  Counting objects of a certain kind (Combinatorics)

How many mazes? how many ordered trees ?

1.4.5  Algebraic structures

That's another kind of structure that can arise in our problems. Addition, multiplication and other algebraic operations are very powerful tools. We will see that such operations can often be defined for other objects that the usual integers or real number.

1.4.6  Making a solution into an algorithm, and implementing it

Part I
Formal Logic

Chapter 2  Propositional Logic

2.1  Introduction

2.1.1  What is a proof ?


Définition 1   A proof is a piece of text written by a human to convince another human that some fact is true.
Problem 1   [1, p. 2]

You have been selected to serve on jury duty for a criminal case. The attorney for the defense argues as follow:

``If my client is guilty, then the knife was in the drawer. Either the knife was not in the drawer, or Jason Pritchard saw the knife. If the knife was not there on October 10, it follows that Jason Pritchard did not see the knife. Furthermore, if the knife was there on October 10, then the knife was in the drawer and also the hammer was in the barn. But we all know that the hammer was not in the barn. Therefore, ladies and gentlemen of the jury, my client is innocent.''
Are you convinced ?

Problems: A good proof consists of: Let's look at a very simple example:
Théorème 1   Let x and y be two integers.

If x is odd and y is odd, then xy is odd.

Proof. Assume x is odd and y is odd.

Let k be an integer such that x=2k+1.

Let l be an integer such that y=2l+1.

Then, xy=(2k+1)(2l+1)=2(2kl+k+l)+1.

Note that 2kl+k+l is an integer.

Conclusion: xy is odd.




2.1.2  Formal and Informal proofs

What do we mean by ``derives logically from the previous ones'' ?

What operations shall we consider as legal ?

To learn more about this, we need a model of what we intuitively consider as true, or logic.

This model we are going to construct is called formal logic.

Formal systems


Définition 2   A formal system is build by providing: A string that can be obtained from the axioms by applying rewriting rules is called a theorem of the formal system.

The proof of a theorem is a description of the axioms and rules used to get the theorem.

The set of all theorems is called the language defined by the formal system.
Exemple 1   The MIU formal system[2]
A formal system does not need to have any meaning or semantic. It's pure syntax.

We will build formal logic as a formal system, with a meaning! Then, any theorem of this formal system shall be interpreted as true.

We will have to be very careful with the choice of the axioms and rules!

Proofs and programming

Writing a proof and a writing a program are very similar:


Proofs Programming Purpose
Theorem Function prototype How to use it
Proof Function definition How it works
Intuitive proof Comments Explanation for the reader
Informal proof Program in a high level language Human readable
Formal proof Program in assembly language Machine readable
Checking an informal proof Compiling Human readable -> Machine readable



This comparison is not gratuitous. There are deep links between proofs and programming which have been studied a lot in the last decades. This is called the Curry-Howard correspondence.

2.2  Statements, Symbolic Representation, and Tautologies

As a first step, let's define logic formulas and their interpretation.

2.2.1  Statements and Propositions


Définition 3   A statement (or proposition) is a sentence which is either true or false.
Exemple 2   Which sentences below are statements ?
Notation 1   A, B, C: symbols representing a statement.

Each of those symbols can be given a truth value, either True (T for short) or False (F for short).

1 is a statement if truth value True.

0 is a statement if truth value False.

2.2.2  Connectives

How can we combine two statements ?

And (conjunction), or (disjunction)


Exemple 3   ``The sky is cloudy'': A. ``It's raining'': B.
Définition 4   The truth table of a formula describes when it's true or not, given the truth value of the symbols.


A B A/\ B A\/ B
T T    
T F    
F T    
F F    


Exclusive or


Exemple 4   ``Cheese or desert''

You get cheese: A

You get desert: B
Définition 5   A exclusive or B: A xor B.

Truth table:


A B A xor B
T T  
T F  
F T  
F F  


Implication


Exemple 5   ``If I get my driver license, I will open a bottle of champagne''.

``I get my driver license'': A.

``I open a bottle of champagne'': B.
Définition 6   A implies B: A-> B.

Truth table:


A B A-> B
T T  
T F  
F T  
F F  


Why this should be true: Why this should be false:

This one can be tricky. To help you make up your mind, here are some examples: Well, as strange as it can sound, F-> T is a true formula.

If you start from an utterly false hypothesis, you can prove anything.

``Avec des si, on pourrait mettre Paris en bouteille''

``With ifs, Paris could be put in a bottle''
Remarque 1   A-> B and B-> A are not the same!
Sounds stupid ?

Look carefully around you! This is the most common logic error in peoples argumentations.

And it's not always an involuntary error.
Exercice 1   Give the antecedent and the consequent in the following sentences

Equivalence


Exemple 6   The knight will win if and only if his armor is strong

The knight will win: A.

His armor is strong: B.

This sentence contains two informations:
Définition 7   A is equivalent to B: A<-> B.

Truth table:


A B A<-> B
T T  
T F  
F T  
F F  


Not

So far we defined binary connectives, that is connectives which took two arguments.

Here is now a unary connective, taking just one argument.
Exemple 7   It will not rain tomorrow

The knight will win: A.

His armor is strong: B.

This sentence contains two informations:
Définition 8   not A: A' (more usual notation: ¬ A)

Truth table:


A A'
T  
F  

2.2.3  Complex Well Formed Formulas


Définition 9   A formula is a string of A well formed formula (or wff) is a formula which satisfies certain syntax rules.
Notation 2   Symbols representing wff: P, Q, R.

Order of precedence

The formula A/\ B-> C' is ambiguous. It can be read as: Solution 1: always put all parenthesis (not very readable).

Solution 2: put an order of precedence between the operators:
  1. Connectives within parentheses, innermost parenthesis first
  2. '
  3. /\, \/
  4. ->, <-
  5. <->
With this order of preference, A/\ B-> C' unambiguously refer to (A/\ B)->(C)'.

Evaluation of a wff

From the truth values of the basic statements, and the elementary truth tables, one can evaluate the truth value of a wff.
Exemple 8   A/\ B-> C', with A true, B false and C true:

A/\ B: false

C': false

A/\ B-> C': true
There is a recursive algorithm to compute the evaluation of a wff.

Truth table of a wff

This yields an algorithm for computing the truth table of a wff.


A B C A/\ B C' (A/\ B)->(C')
T T T      
T T F      
T F T      
T F F      
F T T      
F T F      
F F T      
F F F      


Problem 3   What's the size of a truth table?

Problem 4   Can any truth table be obtained by a wff?

2.2.4  Tautologies and Contradictions


Définition 10   A tautology is a statement that is always true.

A contradiction is a statement that is always false.
Exemple 9   A\/ A'

``Today the sun shine or today the sun does not shine''.
Exercice 2   Are the following wff tautologies or contradictions ?
  1. A/\ A'
  2. A<-> A
  3. (A/\ B)<->(B/\ A)
  4. (A/\ B)-> A
Algorithm to check for a tautology?

Compute the truth table!

It's slow (2n, where n is the number of propositions), but it works.

For certain simple forms of propositions, there is a much faster algorithm (see [1, Tautology test, p. 13]).
Exemple 10   Is [(A/\ B-> C')/\(E<- D)]<->[(E<- D)/\(A/\ B-> C')] a tautology ?

Let P:=(A/\ B-> C') and Q:=(E<- D).

The formula above is [P/\ Q]<->[Q/\ P].

Let's prove it's a tautology.

Take some truth values for A, B, C, D, E.

P and Q will then have some truth value.

But we know that (A/\ B)<->(B/\ A) is a tautology.

So [P/\ Q]<->[Q/\ P] will be true!

We don't actually need to compute the truth table of P and Q.
Remarque 2   Whenever you have some tautology, if you replace ALL occurrences of some basic statement (say A) by a more complicated wff, you still get a tautology.

2.2.5  Equivalence of wff

Let P and Q be two wff, and suppose P<-> Q is a tautology.

Then P and Q have the same truth table.
Définition 11   P and Q are equivalent (noted P <=> Q) if they have the same truth table.
Remarque 3   Writing P<-> Q or P <=> Q is different.

In the first case, you just represent a formula, which can be true or false.

In the second case, you claim that the wff P<-> Q is a tautology.

Basic equivalent wff

What is the negation of ``Peter is tall and thin'' ?


Identity (id) A\/0 <=> A
  A/\1 <=> A
Complement (comp) A\/ A' <=> 1
  A/\ A' <=> 0
Commutativity (comm) A\/ B <=> B\/ A
  A/\ B <=> B/\ A
Associativity (ass) (A\/ B)\/ C <=> A\/(B\/ C) <=> A\/ B\/ C
  (A/\ B)/\ C <=> A/\(B/\ C) <=> A/\ B/\ C
Distributivity (dist) A\/(B/\ C) <=> (A\/ B)/\(A\/ C)
  A/\(B\/ C) <=> (A/\ B)\/(A/\ C)
Double negation (dn) A'' <=> A
De Morgan's Law (dm) (A\/ B)' <=> A'/\ B'
  (A/\ B)' <=> A'\/ B'
Implication (imp) A'\/ B <=> A-> B


Remarque 4   Notice the duality between \/ and /\.

Unlike + and · they play a perfectly symmetric role in all formulas.

More equivalent wff using substitution


Exemple 11   (A/\ B)/\1 <=> (A/\ B).
Remarque 5   Let P and Q be equivalent wff.

If you replace all occurrences of some basic statement by another wff, you still get two equivalent wff's.
Exemple 12   A/\(B\/ C) <=> A/\(C\/ B)
Remarque 6   Let P and Q be equivalent wff.

If P appears exactly as a subformula of a bigger wff, then you can substitute P by Q and get an equivalent wff.

What's the point ?

Rewriting a formula to simplify it:
Exercice 3   [1, Example 7 p.12]
If ((outflow > inflow) and not ((outflow>inflow) and (pressure < 1000)))

  Do something;

Else

  Do something else;

EndIf
Write the wwf corresponding to the test.

Rewrite this wwf using equivalence rules.
Electronic circuits and logical gates:
Exercice 4   Build an electronic circuit for (A/\ B)-> C'.

2.3  Propositional logic

2.3.1  Arguments

We have seen propositions, well formed formula for formalizing statements.

We now need to formalize arguments.
Exemple 13   [1, Example 17 p. 28]

Let's formalize the following argument:

``If interest rates drop, the housing market will improve.

Either the federal discount rate will drop, or the housing market will not improve.

Interest rates will drop.

Therefore the federal discount rate will drop.''

Basic statements: Argument: (I-> H)/\(F\/ H')/\ I -> F
Définition 12   An argument is a wff of the form P1/\ P2/\···/\ Pn -> Q.

P1,···,Pn are the hypothesis.

Q is the conclusion.

The argument is valid iff P1/\ P2/\···/\ Pn -> Q is a tautology.
Exercice 5   Prove that the following arguments are valid:
  1. [A->(B-> C)] -> [(A/\ B)-> C]
  2. [(A/\ B)-> C] -> [A->(B-> C)]
Why is this reasonable ?

``If the sun shine then if you don't put sun cream, you will get burned'': A -> (B-> C)

``If the sun shine and you don't put sun cream, then you will get burned'': (A/\ B) -> C
Exemple 14   ``George Washington was the first president of the United States.

Therefore everyday has 24 hours.''
We put some more restrictions to only keep ``meaningful'' arguments.

2.3.2  Proof sequences

So now, how to prove that an argument is a tautology ?
  1. Use the truth table
  2. Use formal logic!
Exemple 15   Let's prove that the argument A\/(A\/ B)' -> (A\/ B') is valid.

We are lazy to compute the truth table.

Instead, we assume that the hypothesis is valid, and use a series of equivalences to deduce that the conclusion is valid.
1. A\/(A\/ B)' (Hypothesis)
2. A\/(A'/\ B') (De Morgan's, 1)
3. (A\/ A')/\(A\/ B') (Distributivity, 2)
4. 1/\(A\/ B') (Complement, 3)
5. (A\/ B') (Identity, 4)

What we just did is called a proof sequence.

This is our first proof using formal logic.
Exercice 6   Prove that the following argument is valid:

(A\/ B)'\/(A'/\ B) -> A'
Définition 13   Formal Logic: wff + set of derivation rules (formal system).
What derivation rules shall we accept?

We want our formal logic to be:

2.3.3  Looking for derivation Rules


Exemple 16   A/\ B -> A
Equivalences rules are not enough.

We can't prove the previous statement, because A/\ B is strictly stronger than A.

We have build equivalence rules from equivalences P<-> Q.

We can build Inference rules from any valid argument P-> Q.


Rule name From Can derive
modus ponens (mp) P, (P-> Q) Q
modus tollens (mt) (P-> Q), Q' P'
conjunction (con) P, Q P/\ Q
simplification (sim) P/\ Q P, Q
addition (add) P P\/ Q


Exemple 17   A/\(A-> B)/\(B-> C) -> C
1. A/\(A-> B)/\(B-> C) (Hypothesis)
2. A (Simplification, 1)
3. A-> B (Simplification, 1)
4. B (Modus ponens, 2, 3)
5. B-> C (Simplification, 1)
6. C (Modus ponens, 4, 5)


Exemple 18   (A->(B\/ C))/\ B'/\ C' -> A'
1. (A->(B\/ C))/\ B'/\ C' (Hypothesis)
2. (A->(B\/ C)) (Simplification 1)
3. (B'/\ C') (Simplification 1)
4. (B\/ C)' (De Morgan's 3)
5. A' (Modus tollens 4, 5)

Exercice 7   Prove the validity of the following arguments using formal logic:
  1. A/\(B-> C)/\[(A/\ B)->(D\/ C')]/\ B-> D
  2. A'/\(A\/ B)-> B
  3. A'/\ B/\[B->(A\/ C)]-> C
  4. A/\ A'-> B
Theorem 1   This formal logic is correct and complete.
The correctness of the formal logic comes from the way we built the rules from valid arguments.

Proving it's complete is far more difficult.

2.3.4  Methods to make it easier

Our logic is complete, but still not very practical to use.

Here are some tricks to make it easier.

Most of the time, the proofs start like this:
1. (A->(B\/ C))/\ B'/\ C' (hyp)
2. (A->(B\/ C)) (Simp 1)
3. (B'/\ C') (Simp 1)
··· ··· ···

The steps 2 and 3 are pretty trivial, and it's reasonable to start directly with:
1. (A->(B\/ C)) (hyp)
2. (B'/\ C') (hyp)
··· ··· ···

The deduction method


Exemple 19   (A-> B)/\(B-> C) -> (A-> C)

The obvious start is:
1. (A-> B) (hyp)
2. (B-> C) (hyp)

But then it's pretty painful:
3. A'\/ B (imp 1)
4. A'\/(B-> C) (add 2)
5. (A'\/ B)/\(A'\/(B-> C)) (con 3, 4)
6. A'\/(B/\(B'-> C)) (dist 5)
7. A'\/ C (mp 6)
8. A-> C (imp 7)

Here it's easier to first rewrite the argument into an equivalent argument.

We have seen that P->(Q-> R) and (P/\ Q)-> R are equivalent.

So we can prove A/\(A-> B)/\(B-> C) -> C instead, which is straightforward:
1. A (hyp)
1. (A-> B) (hyp)
2. (B-> C) (hyp)
3. B (mt 1, 3)
4. C (mt 2, 4)

This trick is called the deduction method.

It's powerful because we have:
Exercice 8   (A-> B)/\[B->(C-> D)]/\[A->(B-> C)] -> (A-> D)

Additional deduction rules

As we have seen, any valid argument could be transformed into a new rule.
Exemple 20   Here are two useful rules.

Rule name From Can derive
hypothetical syllogism (hs) P-> Q, Q-> R P-> R
contraposition P-> Q Q'-> P'



Adding those new rules won't change the power of the formal logic, but can make it more convenient. On the other hand, a minimal formal logic is nice since it's less error prone, and it's easier to remember all the rules.

It's up to you to choose which rules you want to use (and learn).
Exemple 21   (P-> Q)/\(P'-> Q)-> Q.

2.4  Verbal arguments

We can now start checking verbal arguments.
Exemple 22   Let's prove the following verbal argument[1, Example 17 p. 28]:

``If interest rates drop, the housing market will improve.

Either the federal discount rate will drop, or the housing market will not improve.

Interest rates will drop.

Therefore the federal discount rate will drop.''
Exercice 9   Prove the following verbal argument[1, Ex. 30 p. 32]:

``If the program is efficient, it executes quickly.

Either the program is efficient or it has a bug.

However, the program does not execute quickly.

Therefore it has a bug.''

2.5  Summary

2.5.1  Different levels of logic

Three levels for arguments: Any verbal argument based on propositions can be translated into a formal argument.

The propositional logic system is complete and correct:

2.5.2  Syntactic proof versus semantic proof

Testing an argument by computing it's truth table is purely mechanical.

So, what's the point of formal logic ?

Chapter 3  Predicate Logic (sections 1.3, 1.4)

3.1  Introduction


Exemple 23   ``Every man has a brain; Socrate is a man; therefore Socrate has a brain.''

Is propositional logic expressive enough for this sentence ?

What is missing ?

3.1.1  Quantifiers, Predicates, Validity


Exemple 24   ``Every man has a brain''

``For all man, this man has a brain''
New features: constants / variables / quantifier / predicates
Définition 14   Quantifiers: Universal quantifier: (for all x)

Existential quantifier: (there exists x)

Always place the quantifiers inside ( ).

3.1.2  Predicates:


Définition 15   Predicate: a statement that describes a property of a variable
Exemple 25   P(x) : x has a brain

``For all man, this man has a brain''

Translates into (for allx ) P(x)
As in propositional logic, we can build well formed formulas from predicates and logic connectives.
Exemple 26   (for allx ) B(x)-> R(x)': if x is blue, then x is not red.

3.1.3  Domain of interpretation:

If x is a car, the sentence above (for allx ) P(x) is false.

The truth of the sentence depends on where you take x from!
Définition 16   Domain of interpretation:

The collection of objects from which x may be selected
Exemple 27   (for allx ) (x>0)

DOI: all integers

DOI: all integers > 10

DOI: all humans

Exemple 28   For any thing, if it's a man then it has a brain

P(x): x is a man

Q(x): x has a brain

(for allx ) P(x)-> Q(x)
Exercice 10   Write a formula for the following sentence:

``There exists a man which is called Socrate''

3.1.4  N-Ary predicates:


Définition 17   Binary predicate: predicate which takes two variables

N-Ary predicate : predicate which takes several variables

3.1.5  Truth value

Can we define the Truth table of a wff ?
Problem 1   The domain of interpretation may be infinite.
To assess the truth value, we need to know:
  1. What is the domain of interpretation.
  2. What property of elements of the DOI does P(x) represent.
  3. An assignment for each constant.
Définition 18   This is called an interpretation.
Exemple 29   [1, Exercise 1 p. 41]

What is the truth value of the following wffs for this interpretation:

DOI: integers; O(x): x is odd; L(x): x<10; G(x): x>9
  1. (there existsx ) O(x)

    There exists an odd number

  2. (for allx ) [L(x)-> O(x)]

    For any integer x, if x is strictly lower than 10, then x is odd;

    Any integer strictly lower than 10 is odd;

  3. (there existsx ) [L(x)/\ G(x)]

    There exists an integer x such that x is strictly lower than 10 and x is strictly larger than 9

  4. (for allx ) [L(x)\/ G(x)]

    For any integer, either x is strictly lower than 10 or x is strictly bigger that 9
Exercice 11   [1, Exercise 3 p. 41]

Are the following wffs true for this interpretation:

DOI: states of the US.

Q(x,y): x is north of y; P(x): x starts with the letter M; a is "Mississippi".
  1. (for allx ) P(x)
  2. (for allx ) (for ally ) (for allz ) [ (Q(x,y)/\ Q(y,z)) -> Q(x,z) ]
  3. (there existsy ) (there existsx ) Q(x,y)
  4. (for allx ) (there existsy ) [P(y)/\ Q(x,y)]

    For any state x, there exists a state y such that y starts with M and x is north of y.

  5. (there existsy ) Q(a,y)

Exercice 12   Translate the following sentences into wffs, with:

DOI: world; D(x): x is a day; S(x): x is sunny; R(x): x is rainy;

M is "Monday"; T is "Tuesday".
  1. All days are sunny:
  2. Some days are not rainy:
  3. Every day that is sunny is not rainy:
  4. Some days are sunny and rainy:
  5. No day is both sunny and rainy:
  6. It is always a sunny day only if it is a rainy day:
  7. No day is sunny:
  8. Monday was sunny; therefore every day will be sunny:
  9. It rained both Monday and Tuesday:
  10. If some day is rainy, then every day will be sunny:

3.1.6  Dummy variables / free variables:


Définition 19   A dummy variable is a variable which is linked to a quantifier.

The name of the variable is irrelevant.

Same thing as a local variable in a program.
Exemple 30   (there existsx ) Q(x) is the same wff as (there existsz ) Q(z)

(there existsx ) (for ally ) Q(x,y) is the same wff as (there existsz ) (for allt ) Q(z,t) or (there existsy ) (for allx ) Q(y,x)
Définition 20   A variable is free if it is not linked to a quantifier.

Same thing as a global variable in a program.

3.1.7  Validity


Résumé 2   Where are we?
  1. We can build all the wff of predicate logic.
  2. Given a wff P, and an interpretation, we can decide the truth value of P.
Définition 21   Argument: P1/\ P2/\···/\ Pk -> Q
Exercice 13   [1, Exercise 16 p. 35]

Give interpretations to prove that the following wffs are not valid:
  1. (there existsx ) A(x)/\(there existsx ) B(x) -> (there existsx ) [ A(x)/\ B(x) ]
  2. (for allx ) (there existsy ) P(x,y) -> (there existsx ) (for ally ) P(x,y)
  3. (for allx ) [P(x)-> Q(x)] -> (for allx ) [P(x)\/ Q(x)]
  4. (for allx ) [ A(x)' ] <-> [(for allx ) A(x) ]'

3.2  Predicate logic

There is an infinity of interpretations, so there is no algorithm to check the validity of a predicate.

We will have to use REASON:

3.2.1  Universal instantiation:


Exemple 31   We want to be able to prove the following argument:

Every human is mortal; Socrate is a man; Therefore Socrate is mortal.

H(x): x is a human; M(x): x is a mortal; s: Socrate

(for allx ) [H(x) -> M(x)]/\ H(s) -> M(s)
Définition 22   Rule of universal instantiation (ui):

From: (for allx ) P(x)

Can derive: P(s)

Note: s can be any constant.
We decide that this rule is valid, because it is intuitively valid.

Proof sequence for: (for allx ) [H(x)-> M(x)]/\ H(s) -> M(s)
1. (for allx ) [H(x)-> M(x)] (hyp)
2. H(s) (hyp)
3. H(s)-> M(s) (ui 1)
4. M(s) (mp 2, 3)

Exercice 14   Prove (for allx ) [ P(x)-> R(x) ]/\[ R(y)' ] -> [ P(y)' ]

3.2.2  Universal generalization:


Exemple 32   ``Every human is a living being. Every living being is mortal.Therefore every human is mortal.''

H(x): is a human

L(x): is a living being

M(x) is mortal

(for allx ) [H(x)-> L(x)] /\ (for allx ) [L(x)-> M(x)] -> (for allx ) [H(x)-> M(x)]
This is clearly something we want to be able to prove, but we cannot use hypothetical syllogism directly!
Définition 23   Rule of universal generalization (ug)

From: P(s)

Can derive: (for allx ) P(x)

s must be an arbitrary element of the domain.
Exemple 33   (for allx ) [H(x)-> L(x)] /\ (for allx ) [L(x)-> M(x)] -> (for allx ) [H(x)-> M(x)]
1. (for allx ) H(x)-> L(x) (hyp)
2. (for allx ) L(x)-> M(x) (hyp)
3. H(s)-> M(s) (ui 1)
4. L(s)-> M(s) (ui 2)
5. H(s)-> M(s) (hs 3,4)
6. (for allx ) [H(x)-> M(x)] (ug 5)

Exemple 34   s: Socrate; H(x): x is a man; M(x): x is mortal:
1. M(s) (hyp)
2. H(s)'\/ M(s) (add 1)
3. H(s)-> M(s) (imp 2)
4. (for allx ) [H(x)-> M(x)] (ug 3)

Socrate is a mortal, therefore every man is a mortal.
This proof sequence is incorrect: you cannot apply ug at step 4.

Indeed s is Socrate, and not an arbitrary element of the domain.
Exercice 15   Prove the following arguments:
  1. (for allx ) [P(x)/\ Q(x)] -> (for allx ) P(x)/\(for allx ) Q(x)
  2. (for allx ) P(x)/\(for allx ) Q(x) -> (for allx ) (P(x)/\ Q(x))
  3. (for allx ) [P(x)/\(for ally ) Q(x,y)] -> (for allx ) (for ally ) Q(x,y)

3.2.3  Existential instantiation:


Exemple 35   DOI: contents of the fridge.

There exists a fruit; therefore, I can take a fruit.

F(x): x is a fruit

(there existsx ) F(x) -> F(s)
Définition 24   Rule of existential instantiation (ei):

From: (there existsx ) P(x)

Can derive: P(s)

s must be a newly created variable
Exemple 36   (for allx ) [P(x)-> Q(x)] /\(there existsy ) P(y) -> Q(s)
1. (for allx ) [P(x)-> Q(x)] (hyp)
2. (there existsy ) P(y) (hyp)
3. P(s) (ei 2)
4. P(s)-> Q(s) (ui 1)
5. Q(s) (mp 3,4)

3.2.4  Existential generalization:


Exemple 37   DOI: contents of the fridge

I see a fruit, therefore there exists a fruit.

F(s) -> (there existsx ) F(x)
Définition 25   Rule of existential generalization (eg)

From: F(s)

Can derive:(there existsx ) F(x)
Exemple 38   (for allx ) [P(x)-> Q(x)] /\ (there existsy ) P(y) -> (there existsy ) Q(y)
1. (for allx ) [P(x)-> Q(x)] (hyp)
2. (there existsy ) P(y) (hyp)
3. P(s) (ei 2)
4. P(s)-> Q(s) (ui 1)
5. Q(s) (mp 3,4)
6. (there existsy ) Q(y) (eg 5)


Exemple 39   (there existsx ) P(x)/\(there existsx ) Q(x) -> (there existsx ) [P(x)/\ Q(x)]
1. (there existsx ) P(x) (hyp)
2. (there existsx ) Q(x) (hyp)
3. P(s) (ei 1)
4. Q(s) (ei 2)
5. P(s)/\ Q(s) (add 3,4)
6. (there existsx ) [P(x)/\ Q(x)] (eg 5)


We have seen that the previous argument is incorrect:

So, where is the flaw in the following proof ?

For example, s cannot have been created by existential instantiation
Exercice 16   Prove or disprove the following arguments
  1. (there existsx ) (for ally ) Q(x,y) -> (for ally ) (there existsx ) Q(x,y)
  2. (for allx ) (there existsy ) Q(x,y) -> (there existsy ) (for allx ) Q(x,y)

3.2.5  Deduction Method and Temporary Hypothesis:


Exemple 40   P(s)->(for ally ) Q(x,y) -> (for ally ) [P(s)-> Q(x,y)]

3.3  Conclusion

Goal: formalization of arguments and proofs.
Propositional logic:
 

propositions A, B, ...

connectives, well formed formula

truth table

argument valid iff wff is a tautology

proofs: Ex 24, 37

Predicate logic
 

variables, predicates

domain of interpretation

connectives, wff

interpretation

truth table: all possible interpretations (infinite)

argument valid iff wff is true for all possible interpretations

proofs:
Those two logic are correct and complete.

They are still not powerful enough to represent all real life argument.

For this we would need of more powerful logics (2nd order), that allows for quantifying other sets.

Problem: it's often difficult, if not impossible to prove that those logics are complete and correct!

We won't need to go into those details.

We have seen enough low-level logic to help us write safely less formal proofs.

Part II
Proofs

Chapter 4  Proof techniques (section 2.1)

4.1  Theorems and Informal proofs

What we have seen so far:
Argument
P1/\···/\ Pn -> Q
Syntax
how it's written
Semantic
meaning in a given interpretation
Valid argument
 

True for all interpretations

True because of its very structure
Proofs of valid argument are purely based on syntactical rewriting rules.

Only arguments that are true for all interpretations can be proved.

4.1.1  Theorems

We are now interested to work in a particular subject (say integer arithmetic).
Définition 26   A theorem is an argument that is valid in this particular subject.
Exemple 41   If x is even and y is even then xy is even.

E(x): x is even

(for allx ) (for ally ) [E(x)/\ E(y) -> E(xy)]
This argument is true in this context, but not universally true.

How to prove it ?

Implicitly, we add new hypothesis which reflects basic facts of this subject.

For example, we add the following hypothesis: Using those new hypothesis, it's now possible to write a formal logic proof of the theorem.

See [1, Example 4 p. 87]

4.1.2  Formal and informal proofs:

Remember that the goal of a proof is to be read by humans (in particular yourself) in order to convince those humans.

The formal proof above is convincing in the sense that you can check that all the steps are valid. However, it's very difficult to extract the meaning of the proof: The problem is that the keys of the proofs are buried under layers of insignificant details.

So, starting from now, we will write informal proofs:
Définition 27   An informal proof is a narrative descriptions, of the ideas and of the important steps of the proof, without extraneous details.
Exemple 42   A proof of the theorem above could be written as follow:

Proof. Let x and y be two even integers. We can take n and m such that x=2n and y=2m.

Then, xy=2(2nm). Since 2nm is an integer, xy is an even number.


Let see which details we omitted:
  1. Let x and y be two even integers.

    Implicit universal instantiation

  2. We can take n and m such that x=2n and y=2m.

    Implicit universal instantiation for x and y of the definition of an even number

    Implicit existential instantiation for n and m

  3. Then, xy=2(2nm)

    Implicit use of rules of arithmetic

  4. Since 2nm is an integer, xy is an even number:

    Implicit universal instantiation of the definition of an even number

    Implicit universal generalization to get the final result
Problem 1   Which details can we omit, and which not ?
A reader will be convinced by the proof if he can check that he could translate each step of the proof into one or several steps of a formal proof.

So, this all depends on WHO reads the proof!

You should not write your proof for your instructor, but for yourself, and for everybody else in the class.

A good rule of thumb is to imagine yourself rereading the proof in a few month, and to check that even then, you could possibly translate the proof into a formal one.

The difference between formal and informal proofs is very similar to the difference between assembly and, say, C++ or Java. A C++ program is not usable by itself. It's usable because it's possible to translate it into assembly language.

However, there does not exists, and most likely will never exists, a compiler that transforms informal proofs into formal proofs. English is much to rich a language for this.

4.1.3  Formal and informal theorems:

Most of the time, we also won't write theorems as a formal argument, but rather with an English sentence that could be translated into a formal argument:
Théorème 2   Let x and y be two integers. [Some definitions: interpretation]

Assume x and y are even. [Some hypothesis: P1/\···/\ Pn]

Then, xy is even. [Consequent: Q]

4.1.4  To Prove or not to prove

In textbooks, you can be asked: prove that ... Usually, in real life, you first have to find what to prove. Two jobs:
Définition 28   A conjecture is a statement that you guess is true, but that you have not proved or disproved yet.
Classical steps:
  1. Explore some examples
  2. Try to see some pattern emerging
  3. Formulate a conjecture
  4. Try to prove (or disprove it)
Steps 1-3 are inductive reasoning, whereas step 4 is deductive reasoning.

Finding the good questions is as important as solving them !
Exemple 43   Fermat's conjecture.

4.1.5  Some ``research'' around the factorial


Définition 29   Let n be an integer. The factorial of n is the number n!:=n(n-1)···1.

For example, 1!=1 and 4!=4·3·2·1=24.
Problem 2   How big is n! ?

4.2  Proof techniques

We want to prove some argument of the form P -> Q.

4.2.1  Disproof by counter example


Conjecture 1   If n is a positive integer, then n!<n3.

4.2.2  Direct proof


Définition 30   Direct proof
  1. Assume P
  2. Deduce Q
Exemple 44   Prove that if x and y are even, then xy is even.
Exercice 17   Prove that if x and y are even, then x+y is even.

4.2.3  Proof by contraposition


Exemple 45   Prove that if n2 is odd, then n is odd.
Hint: prove instead that if n is even, then n2 is even.
Définition 31   Proof by contraposition:
  1. Assume Q' (the consequent is false)
  2. Prove P' (the antecedent is also false)
This technique relies on the fact that P -> Q is equivalent to Q' -> P'.
Exercice 18   Prove that xy is odd if and only if x and y are odd.

4.2.4  Exhaustive proof


Problem 1   Can a proof by example be valid ?

Yes, if there is a finite number of cases to be treated.
Exemple 46   Propositional logic formula (the truth table is finite)
Définition 32   Proof by exhaustion means that all cases have been exhausted.

(and so are you ...).
Exemple 47   Drawing a figure without lifting the pencil and without retracing a line.

4.2.5  Some ``research'' around rational numbers


Définition 33   A number x is rational if it can be written as p/q, where p and q are integers.
Exemple 48   5, -7/5, 1/-3, 14/4, 7/2, ... are rational.
Problem 2   Properties of rational numbers ?

Remarque 7   If x is rational, it's always possible to choose p and q so that:

Problem 3   Are all numbers rational ?

Problem 4   Assume x and y are rational.
  1. Is x+y rational ?
  2. Is xy rational ?
  3. Is x/y rational ?

Problem 5   Is the square root of an integer a rational number ?

Problem 6   Prove that the square root of 2 is irrational.

4.2.6  Proof by contradiction


Théorème 3   The square root of 2 is irrational.

Proof. Let's assume the square root of 2 is rational.

Let p and q be two integers such that (2)1/2=p/q and p and q are relatively prime.

Then, we have 2=(p/q)2, and so 2q2=p2.

Therefore p2 is even, and we have seen that this implies that p is also even.

Let k be the integer such that p=2k.

Then, we have 2q2=p2=(2k)2=4k2, and so q2=2k2.

It follows that q2 is even, and so q is also even.

Conclusion: p and q are both even.

That's a contradiction, since p and q are relatively prime!


Définition 34   Proof by contradiction
  1. Assume the contrary
  2. Deduce a contradiction
This technique relies on the fact that:
  1. Q/\ Q' is always false
  2. if P->0 is true, then P is false.

4.2.7  Serendipity


Exemple 49   The chess board problem.

4.3  Summary


Goal Technique Name
P -> Q Assume P ; deduce Q. Direct proof/Deduction method
P'-> Q' Prove Q-> P. Proof by contraposition
Q' Assume Q; deduce a contradiction. Proof by contradiction
P<-> Q Prove P-> Q; prove Q-> P.  
P/\ Q Prove P ; prove Q.  
P\/ Q Prove P'-> Q  
(P1\/ P2)-> Q Prove P1-> Q; prove P2-> Q Proof by cases
(for allx ) Q(x) Let x; prove Q(x) ui / ug
(there existsx ) Q(x) Construct a such that Q(a) eg
  Be smart Serendipity



Chapter 5  Induction - Recursion

5.1  Introduction


Définition 35   A sequence S is a list of objects, enumerated in some order:
S(1),S(2),S(3),...,S(k),...

A sequence can be defined by giving the value of S(k), for all k.
Exemple 50   S(k):=2k defines the sequence: 2,4,8,16,32,...
Imagine instead that I give you the following recipe: Can you compute S(2)? S(3) ? S(4) ?

Could you compute any S(k), where k>0.
Proposition 1   The sequence S(k) is fully and uniquely defined by (a) and (b).
Définition 36   We say that S is defined recursively by (a) and (b).
Exemple 51   The stair and the baby.
This is the idea of recursion (or induction), which is very useful in maths and computer science.

It allows to reduce an infinite process to a finite (small) number of steps.
Exemple 52   Define S(k) by S(1):=4.

Problem: how to compute S(2) ?

Exemple 53   Define S(k) by S(k):=2S(k-1)

Problem: both the following sequences satisfies this definition!

Exemple 54   Proof that any integer is even.
Pitfall: Both base case and induction step are necessary !

You need to know how to start, and you need to know how to continue.

5.2  Proofs by induction


Problem 1   Let S be the sequence defined by: Goal: compute S(60)

S(1) = 1 =
S(2) = 1+2 =
S(3) =   =
S(4) =   =
·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·
S(k) = 1+···+2k =

Conjecture 2   S(60)=

The formula S(k)=2k-1 is called a closed form formula for S(k).

It allows to compute S(k) easily, without computing all the previous values S(1),S(2),...  S(k-1).

So, how to prove this conjecture ?
Introduce some notation
 

Let P(k) be the predicate: S(k)=2k-1.

For any positive integer k, P(k) is either true or false.

Look at examples
 
Exercice 19   Try the following:
Now, can you prove P(60)?

5.2.1  First principle of mathematical induction:


Théorème 4   First principle of mathematical induction

Let P(k) be a predicate. If:

(a) P(1) is true

(b) For any k>1, P(k-1) true implies P(k) true

Then: P(k) is true for all k>=1.
Définition 37   P is the inductive hypothesis.

(a) is the base case.

(b) is the induction step.
Exemple 55   Consider the sequence S defined as above by:

(a) S(1):=1.

(b) S(k):=S(k)+2k-1.

Let's prove that for all k, S(k)=2k-1.

Proof. Let P(k) be the predicate S(k)=2k-1.
  1. Base case:

    S(1)=1=2    1-1. So, P(1) is true.

  2. Induction step:

    Let k>1 be an integer, and assume P(k-1) is true: S(k-1)=2    k-1-1.

    Then, S(k)=S(k-1)+2    k-1=2k-1-1+2k-1=2k-1.

    So, P(k) is also true.

    Conclusion: by the first principle of mathematical induction,

    P(k) is true for all k>=1, i.e. S(k)=2    k-1.
Exercice 20   Let S(k):=1+3+5+···+(2k-1). Find a closed form formula for S(k).

Exercice 21   Prove that k!>2k for any k>=4.

Exercice 22   Prove that for any integer k, 22k-1 is divisible by 3.

Exercice 23   Prove that a+ar+ar2+···+arn=a-arn/1-r.

Exercice 24   Find a closed form formula for S(k):=14+24+··· k4.

Hint: the difficulty is to find a suggestion. What tool could you use for this?


Exercice 25   The chess board problem.

5.2.2  Other forms of induction:


Exemple 56   Define the sequence F(n) by:

F(1):=1

F(2):=1

F(k)=F(k-1)+F(k-2), for all k>2.
Exercice 26   Can you compute F(3),F(4),F(5)?
This sequence is the famous and useful Fibonacci sequence.
Problem 2   To compute F(k), you not only need F(k-1), but also F(k-2).

So that does not fit into the previous induction scheme.
That's fine, because to compute F(k), you only need to know the values of F(r) for r<k.
Théorème 5   Second principle of Mathematical induction:

Let P(k) be a predicate. If

(a) P(1) is true,

(b) For any k>1, [ P(r) true for any r, 1<= r<k ] implies P(k) true,

then: P(k) is true for all k>=1.
Exemple 57   Any integer is a product of prime integers

Exemple 58   The coin problem
We did not prove that the first (or the second) principle of induction were valid.

Let's just give an idea of the proof:
Théorème 6   The three following principles are in fact equivalent:
  1. the first principle of induction
  2. (b) the second principle of induction
  3. (c) the principle of well ordering:

    every non empty collection of positive integers has a smallest member.
Problem 3   Is the principle of well ordering valid for Z ? R ? C ?

5.3  Other uses of induction

Induction is a much more general problem solving principle.

If you have a family of problems such that: Then, you can solve by induction any problem in your family.
Exemple 59   Problem: computation of F(k).

Measure of the problem: k.

Value of F(1) is known.

F(k) can be computed from the values of F(k-1) and F(k-2)

Exemple 60   Inductive definition of well formed formulas from formal logic

<basic proposition>: A | B | C | ...

<binary connective>: /\ | \/ | -> | <- | <->

<wff>: <basic proposition> | <wff>' | (<wff>) | <wff> <binary connective> <wff>
This kind of inductive description is called *BNF* (Backus Naur form).
Exemple 61   Recursive proof of a property of wff
Théorème 7   If a wff contains n propositions (counted with repetition: in A\/ A, there are two propositions), then it contains n-1 binary connectives.
Exemple 62   Recursive algorithm for the computation of the value of a wff:
bool function Evaluation(P, C)

// Precondition: P is a wff, C is the context, i.e.

// the truth values of all the basic propositions.

// Postcondition: returns the truth value of P in the // context C

Begin

  If P is a proposition (say A) Then

    Return the truth value of A;

  ElseIf P is of the form (Q) Then

    Return Evaluation(Q, C);

  ElseIf P is of the form Q' Then

    Return not Evaluation(Q,C);

  ElseIf P is of the form Q1/\ Q2 Then

    Return Evaluation(Q1, C)and Evaluation(Q2, C);

  ... // Other binary operators

  Else

    Error P is not a wff;

End;
Remarque 8   There are programming languages that are particularly well adapted to write this kind of algorithms. Actually, the real program would almost look like the pseudo-code. See for example CAML ftp://ftp.inria.fr/lang/caml-light/.

Exemple 63   Bijection between words of parenthesis and forests

5.4  Conclusion

Induction is a fundamental technique for solving problems, in particular in computer science.

It's the mathematical formalization of the divide and conquer approach.

Chapter 6  Proof Of Correctness (Sections 1.6, 2.3)

6.1  Introduction

``Beware of bugs in the above code; I have only proved it correct, not tried it.''

Donald E. Knuth http://www-cs-faculty.stanford.edu/~knuth/
How to check if a program is correct ?

Why checking if a program is correct ?

What is a correct program ?
Définition 38   Specification: precise description of how a program should behave.

A program is correct, if it behaves in accordance with its specifications.
How to check if a program is correct?

6.2  Correctness

6.2.1  Assertions

  ...

  x=sqrt(r);  // r should be >= 0 !

  x=a[i];     // i should be in the correct range

  ...
Définition 39   Assertion: condition on the variables of a program that should be verified at some given step, if the program is running correctly.
Using assert in C/C++:
#include <assert.h>

  ...

  assert(r>=0);

  x=sqrt(r);

  assert((0<=i) && (i<MAX));

  x=a[i];

  ...
Each assertion is automatically checked:
Assertion failed, line 35 of file foo.c
With C++, java and other languages, you can use exceptions instead of assert: Static type checking also makes some kind of assertion checking.

One way or the other, check assertions in your programs.

6.2.2  Specification of a function:

int factorial(int n);

// Preconditions: n is a non-negative integer

// Postcondition: returns n!

...

int factorial(int n) {

  assert(n>=0);

  if (n==0) return 1;

  return n*factorial(n-1);

}
The specification of a program can be formalized as follow:
Exemple 64   Program to compute of a square root
Définition 40   P is correct if (for all X) Q(X)-> R(X,P(X)).

A Hoare triple is just a short hand notation: {Q} P {R}
Exemple 65   {x>=0} y:=sqrt(x);; {y2=x}

6.3  Proof of Correctness

6.3.1  Divide and Conquer

Let P be a big program:
s0

s1

s2

...

sn-1
To prove {Q} P {R}, we break P into elementary steps, and insert assertions that describes the state of the program at each step:
{Q}

s0

{R1}

s1

{R1}

s2

...

sn-1

{R}
P is correct, if each step is correct, i.e. the following Hoare triples hold: To prove that the elementary steps are correct, we will use some syntactic rules, exactly as we did in formal logic.

6.3.2  Assignment rule:

Consider the following Hoare triple: {Q} x:=e {R}
Théorème 8   If from Q you can derive R with x substituted everywhere by e,

then the Hoare triple is valid.
Exemple 66   {x=2} y:=x+1 {y=3}

When substituting, y=3 becomes x+1=3.

From x=2, you can deduce x+1=3.

So this Hoare triple holds.

Exemple 67   {x>0} x:=x+1 {x>1}

Here it can be confusing.

The same name x stands for both the value of x before and after the assignments.

If you get confused, just rename the variable:

{x0>0} x1:=x0+1 {x1>1}

When substituting, x1>1 becomes x0+1>1, which you can deduce from x0>0.

6.3.3  Conditional Rule

Consider the following Hoare triple:
{Q}

if condition B then

  P1

else

  P2

end if

{R}
Théorème 9   If the Hoare triples {Q/\ B} P1{R} and {Q/\ B'} P2 {R} hold,

then the Hoare triple above holds.
Exemple 68   [1, Exercise 11 p. 78]

6.3.4  Loop Rule

Consider the following Hoare triple:
{Q}

while condition B do

  P

end_while

{R}
{Q} describes the state of the program before the loop.

We need to have a predicate which describes the state of the program DURING the loop:

The loop invariant {S}

Most of the time, {Q} will do the job, but not always.
Théorème 10   If the Hoare triple {S/\ B} P {S} holds, then the following Hoare triple will hold:
{S}

while condition B do

  P

end_while

{S/\ B'}

6.3.5  A simple example

Consider this little program:
Product(x,y)

// Precondition: x and y are non-negative integers

// Postcondition: returns the product of x and y

begin 

  i:=0;

  j:=0;

  while ( (i=x)' ) do

    j=j+y;

    i:=i+1;

  end while

  // Assertion: { j = x*y }

  return(j);

end;
It's pretty clear that this algorithm it's correct.

Let's check it anyway to see how it works.

Proof. We need a loop invariant, which will describe the state of the program after k iterations.

A reasonable guess is S : j=iy

Let ik, jk and Sk be the value of i, j and S after k iterations.

Base case: using the assignment rule, i0=0 and j0=0 so S0 holds.

Induction step:

Assume the invariant holds after k-1 iterations: jk-1=ik-1y

We need to prove that the invariant is preserved by the k th iteration.

Otherwise said, we have to check that the following Hoare triple holds:
{Sk-1/\(i=x)'}

 jk:=jk-1+y;

 ik:=ik-1+1;

{Sk}
Let's applying the assignment rule.

By substituting ik and jk by the expressions they have been assigned with, we get:
Sk <=> jk = iky  
  <=> jk-1+y = (ik-1+1)y (By the substitution rule)
  <=> ik-1y+y = (ik-1+1)y (By Sk-1)
  <=> ik-1y+y = ik-1y+y

So, Sk indeed holds.

By induction, after any number k of iterations, Sk still hold.

At the end, both Sk and i=x hold, so, as expected: j=iy=xy


Remarque 9   We have proved that after the end of the execution the result is correct.

But what if the program does not terminate and loop forever?

This is not usually consider a proper behavior.

We only have spoken about partial-correctness.

A full proof of correctness needs also a proof of termination!

6.3.6  A more sophisticated example: The Euclidean algorithm

GCD(a,b)

Begin

// Precondition: a and b are non-negative integers  

// with a>=b.

// Postcondition:

// returns gcd(a,b), the greater common divisor of 

// a and b.

Local variables: i, j, q, r

  i:=a;

  j:=b;

  while j>0 do

    // Assertion: 

    // r is the rest of the integer division i/j

    r:= i mod j;

    i:= j;

    j:= r;

  end while

  // Assertion: i is the gcd of a and b.

  return(i);

end;
Exercice 27   Use the Euclidean algorithm to compute:

GCD(8,8), GCD(14,4), GCD(31,17).
Here the proof of correctness of the algorithm is non-trivial.

Proof. Let ik and jk be the value of i and j after k iterations.

We need to find an invariant which describes the state of the program after each iteration.

Take Sk: gcd(ik, jk)=gcd(a,b).
  1. Base case:

    Before the loop, i0=a and j0=b.

    So the invariant S0 holds: gcd(i0, j0)=gcd(a,b);

  2. Induction step:

    Assume Sk-1 holds, that is gcd(ik-1, jk-1)=gcd(a,b).

    We just need to prove that gcd(ik, jk)=gcd(ik-1, jk-1).

    By the assignment rule, we have: So, by the definition of the integer division, we have:
    ik-1=qjk-1+jk
    for some integer q.
    1. Assume x divides both ik and jk.

      Then, of course jk-1, since jk-1=ik.

      By the equation above, x also divides ik-1.

    2. Assume x divides both ik-1 and jk-1.

      Then of course x divides ik.

      Once again, using the equation above, x also divides jk

    Therefore, gcd(ik, jk)=gcd(ik-1, jk-1)=gcd(a,b), as wanted.

  3. At the end:

    By induction, the loop invariant S still holds: gcd(i, j)=gcd(a,b)

    Moreover, the loop condition failed: j=0.

    So, gcd(a,b)=gcd(i, j)=gcd(i, 0)=i, as expected.



6.4  Conclusion

6.4.1  A note on automatic program proving:

6.4.2  Check assertions in your programs!

Chapter 7  Analysis of Algorithm (Section 2.5)


Exemple 69   Finding an element in a list.

Computing the nth Fibonacci number F(n).
Problem 1   How long will my program take to execute ?

How much memory do I need ?

How efficient is my algorithm ?

Is it the best one ?

Which algorithm should I choose ?
Goal: "measure" the quality of an algorithm:

7.1  Complexity of an algorithm: Measuring time


Définition 41   Decide which operations are basic (i.e. multiplications).

Complexity of the algorithm: how many basic operations are needed.
Exemple 70   Sequential search
SequentialSearch(x,l)

// Preconditions:

// - l is a list ["bonjour","car","hello","juggler"]

// - x is a string

// Postcondition: return true iff x is in the list

Begin

  // compare successively x with l[1], l[2], ..., l[n]

  For i From 1 To n Do

    If (x=l[i]) Then Return TRUE; EndIf

  EndFor;

  Return FALSE;

End;
Basic operations: comparison of two strings.

How many operations ? Worst case: n basic operations

Average case: depends on the probability for x to be in the list. Difficult !

Résumé 1   n: size of the data (here, the length of the list)

Worst case: maximum number of operations for a data of size n.

Average case: average number of operations for a data of size n (difficult)
Exemple 71   Binary search

A non sorted dictionary is useless!!!
BinarySearch(x, l)

// Preconditions:

// - l is sorted ["bonjour","car","hello","juggler"]

// - x is a string

// Postcondition: return true iff x is in the list

Begin

  If n=1 Then

    Return x=l[1];

  ElseIf x <= l[n/2] Then

    Return BinarySearch(x, [l[1], ..., l[n/2]]);

  Else

    Return BinarySearch(x, [l[n/2]+1, ..., l[n]]);

  End if

End
Basic operation: comparison of two strings.

How many operations ?


n operations
1  
2  
4  
8  
16  



For n, there is at most k operations, where k is the smallest integer such that 2k-1>= n.

log(n): logarithm of n other base 2

Number of operations: log(n)

7.1.1  How precise ?

The estimate above does not give a precise measure of the time needed.

It depends in particular on: A precise measure of the time is often hard to obtain.

Most of the time, to decide between to algorithms, a rough order of magnitude is enough.

Draw the graphs to get an idea if there are big differences
Définition 42   An algorithm is of complexity O(n5) if it needs less than Cn5+K operations to execute, where C and K are some constant.
Worst case analysis is usually easier. It is important if your need a warranty on the time needed for each data (e.g.: real time data acquisition).

Average case analysis is more difficult. It is important when running over a large sample of data.

7.1.2  Case study: the Fibonacci sequence

Here is a program written in MuPAD www.mupad.de (free Computer Algebra system).

It present different implementations of the computation of the Fibonacci sequence.
/*

fibonacci_rec           (n: Dom::Integer);

fibonacci_rec_remember  (n: Dom::Integer);

fibonacci_loop_array    (n: Dom::Integer);

fibonacci_loop          (n: Dom::Integer);

Precondition: n non negative integer

Postcondition: returns the nth fibonacci number

Also increments the global variable operations.

*/

fibonacci_rec:=

proc(n: Dom::Integer)

begin

  if n=0 then return(1); end_if;

  if n=1 then return(1); end_if;

  operations:=operations+1; // Count operations

  return(fibonacci_rec(n-1)+fibonacci_rec(n-2));

end_proc:

 

fibonacci_array:=

proc(n:Dom::Integer)

  local i, F;

begin

  if n=0 then return(0); end_if;

  if n=1 then return(1); end_if;

  F[0]:=0;

  F[1]:=1;

  for i from 2 to n do

    operations := operations+1; // Count operations

    F[i] := F[i-1] + F[i-2];

  end_for;

  return(tableau(n));

end_proc:

 

fibonacci_loop:=

proc(n:Dom::Integer)

  option remember;

  local i, value, previous, previousprevious;

begin

  if n=0 then return(0); end_if;

  if n=1 then return(1); end_if;

  previous:=0;

  value:=1;

  for i from 2 to n do

    operations := operations+1;   // Count operations

    previousprevious:= previous;

    previous        := value;

    value           := previousprevious+previous;

  end_for;

  return(value);

end_proc:

 

fibonacci_rec_remember:=

proc(n: Dom::Integer)

  option remember;

begin

  if n=0 then return(0); end_if;

  if n=1 then return(1); end_if;

  operations  := operations+1;   // Count operations

  return(fibonacci_rec_remember(n-1)+ 

         fibonacci_rec_remember(n-2)  );

end_proc:

printentry:=

proc(x)

begin

  userinfo(0, NoNL, x);

  userinfo(0, NoNL, "t");

end_proc:

 

for n from 0 to 30 do

 

  printentry(n);

    

  operations:=0;

  printentry(fibonacci_rec(n));

  printentry(operations);

    

  operations:=0;

  fibonacci_array(n);

  printentry(operations);

    

  operations:=0;

  fibonacci_loop(n);

  printentry(operations);

    

  operations:=0;

  fibonacci_rec_remember(n);

  printentry(operations);

  // Clear remember table;

  fibonacci_rec_remember:=

    subsop(fibonacci_rec_remember,5=NIL);

    

  print();

end_for:


Figure 7.1: Measurement of the complexity of the different implementations of the Fibonacci sequence



Problem 2   Why is Fibonacci rec so slow ? (Trace its execution)

How to avoid this?

Don't throw away the results !

The remember option.
Time consumption: Memory consumption: Easiness to write:

7.2  The P=NP conjecture

7.2.1  Case study: Satisfying a well formed formula of propositional logic

We consider a well formed formulas of propositional logic.
Définition 43   A choice of truth values for A, B, C, ... satisfies P if P evaluates to true.
Exemple 72   A true and B true satisfies A/\ B.

A true and B false do not satisfy A/\ B.
Problem 1   Given the truth values of A, B, C, ... check if they satisfy P.

Algorithm ?

Complexity ?
Définition 44   A wff P is satisfiable if at least one choice of truth values for A, B, C, ... satisfies P.

I.e. P is not a contradiction.
Exemple 73   A/\ B is satisfiable, whereas A/\ A' is not.
Problem 2   Testing if a wff P is satisfiable.

Algorithm ?

Complexity ?

Is this the best algorithm ?

Does there exist a polynomial algorithm ?

That's an instance of a problem where:
Exemple 74   Checking if the solution of a crossword puzzle is correct is easy.

Solving the crossword puzzle is not !

Exemple 75   Backpack problem with size=23, and objects=5,7,7,20,17,5,11,5,19,14.

7.2.2  Polynomial and Non Deterministic Polynomial problems


Définition 45   Problems as above are called NP (Non-deterministic Polynomial)

P: collection of all polynomial problems

NP: collection of all NP problems
Problem 3   P = NP ?

In other words:

If it's easy to check a potential solution of a problem,

is there necessarily an easy way to find the solution ?

Intuitively, no. This cannot be true.

Well, despite a lot of research, we still have no proof!

This is the main problem of theoretical computer science since 30 years.

So, this is YOUR job to find the solution !

Part III
Sets and Combinatorics

Chapter 8  Sets (section 3.1 )

8.1  Introduction

Problem p 161

Goal:

8.2  Sets and basic manipulations of sets

8.2.1  Definition


Définition 46   A set A is a collection of objects.
Defining property: you can ask whether an object a belongs to A or not.

Objects or elements: a,b,c,....

Sets: A,B,C,....

Predicates: Two sets A and B are equal (A=B) if they contain the same elements:
(for all x)(xin A)<=>(xin B)

8.2.2  How to define a set S?

You have to describe which elements are in the set S and which are not. Some usual sets:

8.2.3  Relationships between sets

Exercice 28   [1, Exercise 10 p. 117]
R:={1,3,pi,4,1,9,10},  S:={{1},3,9,10}

T:={1,3,pi},  U:={{1,3,pi},1}
  1. Sincluded in or equal to R?
  2. 1in R?
  3. 1in S?
  4. 1included in or equal to U?
  5. {1}included in or equal to T?
  6. {1}included in or equal to S?
  7. Tincluded in R?
  8. {1}in S?
  9. Øincluded in or equal to S?
  10. Tincluded in or equal to U?
  11. Tin U?
  12. Tnot in R?
  13. Tincluded in or equal to R?
  14. Sincluded in or equal to{1,3,9,10}?

8.2.4  The powerset of a set

The powerset (S) of a set S is the set of all subsets of S.
Exemple 76   What are the elements of the following powersets ?
  1. ({1,2})=
  2. ({1})=
  3. (Ø)=
Exercice 29   What is the size of (S) if S has n elements ?

8.2.5  Binary and unary operations


Définition 47   ¤ is a unary operation on a set S if for every element x of S, ¤ x exists, is unique and is a member of S.

¤ is a binary operation on a set S if for every ordered pair (x,y) of elements of S, x¤ y exists, is unique and is a member of S.
Examples:
  1. is +a binary operation on N ?
  2. is +a binary operation on {0,1,2}?
  3. is ×a binary operation on {0,1}
  4. is -a binary operation on N ?
  5. is /a binary operation on Z ?
  6. are +,-, and ×binary operations on Q ?
  7. are +,-, ×and /binary operations on Q*?
  8. is (x)1/2 a unary operation on R+ ?
  9. are /\, \/, ->, ', ... operations on { true,false}? on wff ?
A binary operation can be defined by its multiplication table.
Exemple 77   ({ true,false},/\)

/\ false true
false false false
true false true



An operation does not necessarily need to have a particular meaning.
Exemple 78   ({2,5,9},¤)


¤ 2 5 9
2 2 5 2
5 2 9 5
9 9 2 5



5¤9=?

8.3  Operations on sets

8.3.1  The universe of discourse

We have seen operations on numbers, or other objects.

We can also define operations on sets (union, intersection, ...).

We need a set that contains all the sets we want to deal with.

It would be tempting to consider the set of all sets.
Problem 1   Let S be the set of all sets that does not contain themselves.

Does S contain itself ?
There is a strange loop here which yields a contradiction: S cannot exist.

For a similar reason, the set of all sets cannot exist.

See Gödel Esher Bach[2] for a lot of similar fun stuff with strange loops.

That's been a major source of trouble and work a century ago, when mathematicians tried to define a strong basis for set theory.

To be safe, we always work inside a set big enough to contain all the sets we need, but small enough to avoid the strange loop above.
Définition 48   This set is the universal set, or the universe of discourse.
We define operations on the powerset of the universal set.

8.3.2  Union, intersection, complement and Cartesian product

We define operations on subsets of the universe of discourse.
Définition 49   The union of A and B is the set:
Aunion B:={ x |  xin A or xin B}


Définition 50   The intersection of A and B is the set:
Aintersect B:={ x |  xin A and xin B}


Définition 51   The complement of A is the set:
A':={ x |  xnot in A}


Définition 52   The set difference of A and B is the set:
A-B:={ x (xin A) and (xnot in B)}


Définition 53   The Cartesian product (or cross product) of A and B is the set:
A× B:={(x,y) |  xin A,yin B}

Notation 2   A2=A× A is the set of all ordered pairs of elements of A;

An=A×···× A is the set of all n-uples of elements of A.
Définition 54   Venn diagrams.
Exercice 30   Let A:={1,2} and B:={2,3,4}.
  1. Aunion B=,
  2. Aintersect B=,
  3. A-B=,
  4. A'= (assuming that the universe of discourse is {1,2,3,4}),
  5. A× B=,
  6. A3=.

Exercice 31   Let A be a set of size n, and B a set of size m.
  1. what is the size of Aunion B:
  2. what is the size of Aintersect B:
  3. what is the size of A' ?
  4. what is the size of A× B :

8.3.3  Set identities


Proposition 2   Let A and B be to sets. Then,

Aintersect B=Bintersect A (commutative property)

Proof. xin Aintersect B

<=>(xin A)/\(xin B) by definition of intersect

<=>(xin B)/\(xin A) by commutativity of /\

<=> xin Bintersect A by definition of intersect


The commutativity of intersectderives directly from the commutativity of /\.

All identities on logic operators induce identities on set operators.
Proposition 3   Let A, B, and C be two sets. Then,

Aunion B=Bunion A (commutative property)

Aintersect B=Bintersect A (commutative property)

(Aunion B)union C=Aunion(Bunion C)=Aunion Bunion C (associative property)

(Aintersect B)intersect C=Aintersect(Bintersect C)=Aintersect Bintersect C (associative property)

Aunion A'=S (complement, S is the universe of discourse)

Aintersect A'=Ø (complement)

(Aunion B)'=A'intersect B' (de Morgan's)

(Aintersect B)'=A'union B' (de Morgan's)

A-B=Aintersect B'

8.4  Countable and uncountable sets

8.4.1  Enumerations

If a set S has k elements, these can be listed one after the other:
s1,s2,...,sk

Définition 55   s1,s2,...,sk is called an enumeration of the set S.
Exemple 79   1,5,4,3, 5,1,3,4, and 4,1,3,5 are enumerations of the set {1,5,4,3}.
When a set S is infinite, you can not enumerate all of it's elements at once.

However, some times, you can still pickup a first element s1, then a second s2, and so on forever. This process is an enumeration of the elements of S if:
Exemple 80   0,1,2,3,4,... is an enumeration of the non-negative integers.

8.4.2  Denumerable and Countable sets


Définition 56   A infinite set S is denumerable if it has an enumeration
s1,s2,...,sn,...

A set S is countable if it's either finite or denumerable.
Exemple 81   Are the following sets countable ?
  1. The set of all students in this class.
  2. The set N of the non-negative integers (enumeration: 0,1,2,3,4,...);
    Actually, the order does not need to be logical.
    This is a perfectly legal enumeration: 0,10,5,11,4,2,17,2,1,28,3
  3. The set of the even integers (enumeration: ;
  4. The set of the prime integers (enumeration: ;
  5. The set Z of the integers (enumeration: );
  6. The set N×N

    (e.g. all points in the plane with non-negative integer coordinates):





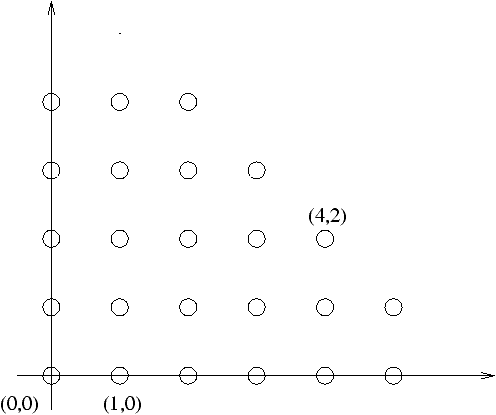
  7. Enumeration: (0,0),(0,1),(1,0),(2,0),(1,1),(0,2),(3,0),...
  8. The set Z×Z of all points in the plane with integer coordinates:





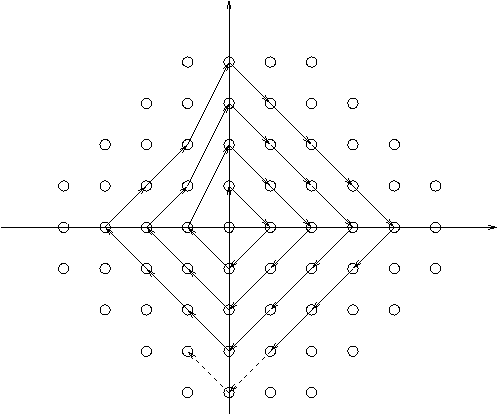
    Enumeration: (0,0),(0,1),(1,0),(0,-1),(-1,0),(2,0),...

  9. The set Q of rational numbers:

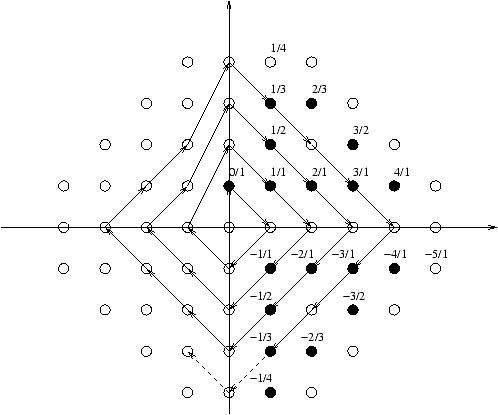
Théorème 11   The following sets are countable:
  1. Any subset Aincluded in B of a countable set B.
  2. The union Aunion B of two countable sets A and B is countable.
  3. The union A1union A2union···union Ai of a finite number i of countable sets A1,...,Ai.
  4. The union A1union A2union···union Aiunion···of a countable number of countable sets.
  5. The cross product A× B of two countable sets A and B is countable.
  6. The cross product A1×···× Ai of a finite number of countable sets A1,...,Ai.

Proof. Enumerations of those sets can be constructed in the following way:


  1. Enumerate the elements of B, and ignore those that are not in A.
  2. Enumerate the elements of A and B alternatively (a1,b1,a2,b2,...).
  3. Induction, using 2.
  4. As for N×N: a1,1,a2,1,a1,2,a3,1,a2,2,a1,3,... (ai,j is the jth element of Ai).
  5. As for N×N: (a1,b1),(a1,b2),(a2,b1),(a1,b3),(a2,b2),(a3,b1),....
  6. Induction, using 5.

8.4.3  Uncountable sets ?


Remarque 10   All the sets we have seen so far are countable.
Problem 1   Are there any uncountable sets ?
Théorème 12   (Cantor) R is uncountable.
Lemme 1   Any real number xin[0,1) can be written uniquely in decimal form:
x=0.d1d2d3d4··· di···,
where the di are digits between 0 and 9, and the sequence does not end by an infinite number of 9.
Exemple 82   Here is how some classical numbers can be written:
Let's jump to the proof of the theorem, without detailing the proof of this lemma.

Proof. (Of the theorem): Cantor diagonalization method.

It's sufficient to prove that [0,1) is not countable.

Let's do this by contradiction: assume [0,1) is countable.

Let s1,s2,...,si,... be an enumeration of [0,1).

Goal: construct an element which is not in this enumeration.

Using the lemma, we can write the si as follow:
s1 = 0,
d1,1
d1,2 d1,3 d1,4 d1,5 ···
s2 = 0, d2,1
d2,2
d2,3 d2,4 d2,5 ···
s3 = 0, d3,1 d3,2
d3,3
d3,4 d3,5 ···
s4 = 0, d4,1 d4,2 d4,3
d4,4
d4,5 ···
s5 = 0, d5,1 d5,2 d5,3 d5,4
d5,5
···
·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·  
 · 
  ·

We want to construct an element x which is not in this enumeration.

Let's look at an example:
s1 = 0,
1
5 7 3 5···
s2 = 0, 0
0
4 7 3···
s3 = 0, 4 5
7
0 3···
s4 = 0, 9 7 3
5
7···
s5 = 0, 4 3 8 1
0
···
·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
·		 ·
·
··  
 · 
  ·
               
x = 0, 0 1 0 0 1···

The trick : let xi=1 if di,i=0 and xi=1 else.

Then, x!= s1. But also, x!= s2, x!= s3, ...

Therefore x is indeed never enumerated! Contradiction!

Conclusion: [0,1) is not countable.


Remarque 11   We can deduce that many sets like C, or [5.3,10) are uncountable.

A similar proof can be used to prove that many other sets are uncountable.

This includes the set of all infinite strings, or the set (N) of all subsets of N.
Résumé 2   We have a hierarchy of bigger and bigger sets:
  1. The empty set
  2. Finite sets (the empty set, sets with 1 element, sets with 2 elements, ...)
  3. Denumerable sets: N, Z, Q, ...
  4. Uncountable sets: R, C, ...
  5. ...
Problem 3   Is there any set bigger than N and smaller that R? Nobody knows!

8.5  Conclusion

We are now done with basic properties of sets. We have seen enough formalism

to go on to the next section, Combinatorics:
How to count the objects in a finite set ?

Chapter 9  Combinatorics (section 3.2...3.5)

9.1  Introduction

Goal: answer ``How many ?'' questions: Applications:

9.2  Counting

9.2.1  Preliminaries


Définition 57   The size of a finite set is the number of elements in this set.

The size of S is denoted by |S| (or, often in the literature, # S).
Note 1   In the sequel, we only consider finite sets !
A``how many ?'' question is usually formalized as follow:
  1. Define the set S of the objects to be counted
  2. What is the size of S ?
Techniques to answer this question:

9.2.2  The addition principle


Exemple 83   A small company wants to know how many computers it owns, given that it owns 5 Mac's, and 3 UNIX stations.

Let: Then, C=Munion U.

What is the size of C ?
| C | = | M | + | U | =5+3=8

Théorème 13   (Addition principle) Let A and B be disjoint sets (e.g. Aintersect B=Ø). Then:
| Aunion B | = | A | + | B | .

Exemple 84   Imagine 2 of the 5 Mac's are actually running Linux.

What is the size of C ?

Well, |C|=6<8.
So, the disjoint hypothesis is important !

What to do when the sets are not disjoint ?
Théorème 14   Let A and B be two sets. Then:
| Aunion B | = | A | + | B | - | Aintersect B | .


Proof. We just have to split A, B, and Aunion B into unions of disjoint subsets:
A=(A-B)union(Aintersect B)

B=(B-A)union(Aintersect B)

Aunion B=(A-B)union(Aintersect B)union(B-A).

(Practice: draw and prove those set identities!).

Then,
| A | + | B | - | Aintersect B |
=
( | A-B | + | Aintersect B | )+( | B-A | + | Aintersect B | )- | Aintersect B |
  =
| A-B | + | Aintersect B | + | B-A |
  =
| Aunion B |


Exemple 85   In the example above, |C|=|M|+|U|-|Mintersect U|=5+3-2=6.
Exercice 32   There are 24 students in a class, all of them are math majors or computer science major. 10 are math majors, and 20 are computer science majors. How many double-major are there in this class ?

9.2.3  The multiplication principle


Exemple 86   You are a car dealer. For each car you sell, you propose several options (color, 2WD/4WD, airbag, ABS, radio, ...). Of course, you would like to always have all possible combinations of options in stock. On the other hand, you cannot afford to store too many cars in your parking lot. So you need to know how many possible combinations of options there are. How many combinations are there ?

First solution: draw a decision tree.

The choices are independent!

The number of sub-branches at each level is constant.

Therefore, we have 2·3=6 choices.

Let's formalize this.

Let C be the set of all choices. Each choice can be represented by a couple.

For example a yellow 2WD car with black seats can be represented as:
(2,Y)

So, C can be viewed as the cross product:
{2,4}×{ B,Y,G}.

Théorème 15   Let A and B be two sets. Then,
| A× B | = | A | · | B | .

Exemple 87   In the example above, |C|=|{2,4}×{ B,Y,G}|=|{2,4}|·|{ B,Y,G}|=2·3=6.
Exercice 33   How many possible different phone numbers are there ?

Strings

Strings are commonly used objects in computer science.

``how many'' questions often be translate into questions about sets of strings.
Définition 58   Let S be a set, that we call alphabet.

Elements of S are called letters.

A string over S is a sequence (s1,s2,...,sn) of elements of S.

lambda:=() is the empty string.

The set of all strings of length n is Sn=S×···× S.

The set of all finite strings over S is denoted S*.

A language is a set of strings.
Exemple 88   Let S:={0,1}. A string over S, like 001001 is called a binary string.

Let S:={ a,b,...,z}. Then bonjour is a string over S of length 7.

A phone number 3032733462 is a string over {0,1,2,3,4,5,6,7,8,9}.

The set of all English words is a language.

Exemple 89   Count the following:
  1. binary strings of length 4?
  2. strings of length n over an alphabet containing p letters ?

9.2.4  Decision trees


Exemple 90   A kid is allowed to pick 3 candies (one after another), out of one jelly bean, one lollipop and 2 gummy bears (one blue, one yellow). In how many ways can he do this ?

Draw a decision tree.

The choices are not independent

The multiplication principle does not apply.

However, the number of choices at each step does not change!

So the answer is: 5·4·3=60.
Exercice 34   Count the following:
  1. Strings of length 4 over {1,2,3,4,5} with no repetitions.
  2. Strings of length n over {1,...,n} with no repetitions.

Exercice 35   How many ways to toss a coin five times without two heads in a row ?

Note: the decision tree is irregular.

9.2.5  Combining those principles together


Exemple 91   Count the following:

Exercise 18-19 p. 195

9.2.6  Principle of Inclusion and Exclusion


Exemple 92   All the guests at a dinner party drink coffee, chocolate or tea; 11drink coffee, 9 drink tea, 10 drink chocolate; 3 drink coffee and tea, 5 drink tea and chocolate; 6 drink coffee and chocolate

Formalization: what is the size of |Aunion Bunion C|?
Generalization ?
Théorème 16   (Principle of Inclusion and exclusion)

Let A1,...,An be n sets. Then,
| A1union···union An |
=
| A1 | +···+ | An |
   
- | A1intersect A2 | -···- | An-1intersect An |
   
+ | A1intersect A2intersect A3 | +··· | An-2intersect An-1intersect An |
   
+(-1)n+1 | A1intersect···intersect An |
  =
 
--
\
/
--
Iincluded in{1,···,n}
(-1)
| I | +1
 
|
|
|
|
 
intersect
iin I
Ai |
|
|
|


Proof. Induction.




9.2.7  Pigeon Hole principle


Exercice 36   It's early in the morning, and you don't want to wake up your significant whatever by turning on the light. You know you only have black and white socks in your drawer. Is it possible to exit the room with at least two socks with the same color ?
Théorème 17   (Pigeon hole principle)

If more than k items are placed in k bins, then at least one bin has more than one item inside.
Exemple 93   How many people do you need to have in a room to ensure at least two of them have the same birthday ?

9.2.8  Permutations: sequences without repetitions


Exemple 94   How many ways to choose a committee with 1 president and 1 vice-president out of a group of n persons.

This amount to find the number of strings of length 2 over a set of size n, without repetitions. This is n(n-1).
Définition 59   We denote by P(n,k) the number of strings of length k over a set of size n without repetitions.
Exemple 95   P(n,0)= , P(n,1)= , P(n,n)= , P(1,2)= .

Théorème 18   P(n,k)=n(n-1)···(n-k+1)=n!/(n-k)!.

9.2.9  Combinations


Exemple 96   How many ways to choose 3 voluntaries out of a group of 5 persons?
Définition 60   We denote by C(n,k) the number of subsets of size k of a set of size n.
Exemple 97   C(n,0)= , C(n,1)= , C(n,n)= , C(1,2)= .

Théorème 19   C(n,k)=n(n-1)···(n-k+1)/k(k-1)···1=n!/k!(n-k)!.
Exemple 98   Ex. 51 p. 210:

A committee of 8 students is to be selected from a class consisting of 19 freshmen and 34 sophomores.
  1. In how many ways can 3 freshmen and 5 sophomores be selected?
  2. In how many ways can a committee with exactly 1 freshman be selected?
  3. In how many ways can a committee with at most 1 freshman be selected?
  4. In how many ways can a committee with at least 1 freshman be selected?
Exemple 99   What is the total number of subsets of S ?
Exemple 100   What is the number of paths between Stratton Hall and Golden Tourism Information center ?

9.2.10  Combinations with repetitions


Exemple 101   In how many ways can you distribute 10 lollipops between 4 kids.
Théorème 20   The number of combinations with repetitions of k elements of a set S of size n is C(n+k-1,n).
Exemple 102   In how many ways can you distribute 10 lollipops between 4 kids, so that every kid get at least one lollipop ?

9.2.11  Summary


Addition principle (A and B disjoint) |Aunion B|=|A|+|B|
Principle of Inclusion-Exclusion |Aunion B|=|A|+|B|-|Aintersect B||A1union···union An|=···
Multiplication principle |A× B|=|A|·|B||Ak|=|A|k
Sequences of k elements of S (|S|=n) nk
Permutations: P(n,k)=n!/(n-k)!
Sequences of k elements of S, w/o repetitions  
Sequences of k elements of {0,1}, w/o successive 1 Fibonacci: F(k)
Combinations: subsets of size k of S C(n,k)=n!/k!(n-k)!
All subsets of S 2n
Combinations with repetitions C(n+k-1,k)



9.3  Properties of binomial coefficients; Combinatorial proofs


Exemple 103   How many subsets of size 14 of a set of size 15 ?
Théorème 21   C(n,k)=C(n,n-k)

Proof.  


  1. Algebraic proof
  2. Combinatorial proof
Définition 61   Combinatorial proof:

Goal: prove that two quantities a and b are equal

Technique:
  1. construct a set A of size a;
  2. construct a set B of size b;
  3. construct a bijection between A and B
Problem 1   Recursive computation of C(n,k) ?

Théorème 22   C(n,k)=C(n-1,k)+C(n-1,k-1)

Proof.  


  1. Algebraic proof
  2. Combinatorial proof
Exemple 104   Compute C(7,4), without calculator.
Définition 62   Pascal triangle:


nk 0 1 2 3 4 5 6 7
0 1              
1 1 1            
2 1 2 1          
3 1 3 3 1        
4 1 4 6 4 1      
5 1 5 10 10 5 1    
6 1 6 15 20 15 6 1  
7 1 7 21 35 35 21 7 1



Théorème 23   C(n,0)+···+C(n,n)=2n

Proof.  


  1. Algebraic proof ?
  2. Combinatorial proof

9.3.1  The binomial theorem


Problem 2   Compute (x+y)n .

Théorème 24   There is a formula for expanding (x+y)n:
(x+y)n =
k=n
--
\
/
--
k=0
C(n,k)xn-kyk
  = C(n,0)xn+C(n,1)xn-1y+C(n,2)xn-2y2+···+C(n,n)yn

9.4  Conclusion

Part IV
Relations Functions and Matrices

Chapter 10  Relations (section 4.1, 4.2 and 4.4)

10.1  Introduction

A mere set of words would not make a good dictionary.

It would be a pain to find a particular word!

A usable dictionary has some structure: the words are sorted.

In general, the more structure a set have, the more useful it is.

A way to bring structure into this set is to describe the relations between its elements, or between its elements and the elements of another set.

In this section we will see how we can formalize and study relations.
Exemple 105   Imagine you want to build a house.

Figure 10.1 shows the tasks that need to be completed.

Figure 10.1: Tasks to build a house

Let S:={ F,W,E,I,O,R} be the set of all tasks.

Problem: can we do the tasks in any order ?

For example, it would be better to build the walls AFTER the foundations!

S in itself does not contain enough information to choose a correct order.

Figure 10.2: Constraints between the tasks to build a house

Set of constraints: rho:={(F,W),(W,O),(W,E),(R,E),(R,I)}.

This set of constraints gives some structure to S, and makes it useful.

10.2  Relations

10.2.1  Definitions


Définition 63   A binary relation on a set S is a subset rho of S× S.

Let x and y be two elements of S.

Then x is in relation with y (denoted x rho y) iff (x,y)inrho.
Exemple 106   Let rho be the relation ``is a prerequisite for'':
rho:={(F,W),(W,O),(W,E),(R,E),(R,I)}

Then, (F,W)inrho, but (I,O)not inrho.

So, F rho W is true, whereas I rho O is false.
A relation can be defined by a property.
Exercice 37   Let S:={1,2,3,4,5}. Draw the relations defined by:
  1. x rho1 y iff x=y;
  2. x rho2 y iff x<= y;
  3. x rho3 y iff x divides y;
  4. x rho4 y iff x-y is even.
Définition 64   A binary relation between two sets S and T is a subset rho of S× T.

A n-ary relation between n sets S1,...,Sn is a subset rho of S1×···× Sn.
Exemple 107   Let M be a set of male and F a set of female students.

We can define the relation ``is married to''.

10.2.2  Basic properties of relations

Is there anything particular about the relation ``is married to'' ?
Définition 65   Let rho be a relation between S and T.









Exemple 108   Is x lower or equal to itself ?
Définition 66   A relation rho on a set S is reflexive iff
(for all xin S) x rho x.


Exemple 109   Assume x is equal to y. Is y equal to x ?
Définition 67   A relation rho on a set S is symmetric iff
(for all xin S)(for all yin S) (x rho y)<->(y rho x).


Exemple 110   Assume x<= y and y<= x. What can you say about x and y?
Définition 68   A relation rho on a set S is antisymmetric iff
(for all xin S)(for all yin S)[(x rho y) and (y rho x)]->(x=y).


Exemple 111   Assume x<y and y<z. What can you say about x and z?
Définition 69   A relation rho on a set S is transitive iff
(for all xin S)(for all yin S)(for all zin S)[(x rho y) and (y rho z)]->(x rho z).


Exemple 112   What are the properties of the following relations
  1. <, <=, =;
  2. ``is married to'';
  3. ``is a friend of'';
  4. ``has the same color than''.

10.2.3  Operations on relations

A relation is basically a set. So, we can use all usual set operations on relations.
Remarque 12   Let S and T be two sets.

The powerset (S× T) is the set of all binary relations between S and T.
Définition 70   Let rho and sigma be two relations between S and T.

We can construct the following new relations:
Exemple 113   Let S:=N.
  1. What is the union of <and =?
  2. What is the intersection of < and >?
  3. What is the union of < and >?
  4. Is <a sub relation of <= ?

10.2.4  Closure of a relation


Exemple 114   Lets come back to the example of the house building.

Figure 10.1: Constraints between the tasks to build a house

Do you have to do the electricity after the foundations ?

Foundations is not a direct prerequisite for electricity.

However, it still needs to be done before electricity.

The relation ``has to be done before'' is transitive, and contains the relation

``is a prerequisite for''. It's the transitive closure of ``is a prerequisite for''.
Définition 71   Let rho be a relation.

The transitive closure of rho is the smallest transitive relation rho*containing rho.
Exercice 38   Draw the transitive closure of ``is a prerequisite for''.
Problem 1   Is there an algorithm for computing the transivite relation of a relation?

Algorithme 2   Construction of the transitive closure rho*.
  1. rho*:=rho;
  2. Find x, y, z such that (x rho*y), (y rho*z), and (x ¬ rho*z);
  3. If no such triple exists, rho*is transitive; Exit;
  4. rho*:=rho*union{(x,z)};
  5. Repeat at step 2.
Remarque 13   The order in which you add the pairs to rho is irrelevant.
Exemple 115   Draw the relation ``has to be done before'' (Figure 10.1).
Définition 72   Let rho be a relation.

The reflexive closure of rho is the smallest reflexive relation containing rho.

The symmetric closure of rho is the smallest symmetric relation containing rho.
Exercice 39   Consider the following relation:



  1. Draw its reflexive closure
  2. Draw its symmetric closure
  3. Draw its transitive closure
  4. Draw its antisymmetric closure

Remarque 14   The antisymmetric closure of a relation cannot be uniquely defined!

10.3  Equivalence relations


Exemple 116   Consider a set of cars, and the relation ``has the same color as''.

What are the properties of this relation?
Définition 73   An equivalence relation is a relation which is
  1. Reflexive
  2. Symmetric
  3. Transitive

Définition 74   Let rho be a relation on a set S, and x be an element of S.

The equivalence class of x is the set [x]of all elements y such that x rho y.
Exemple 117   The equivalence class of a car is the set of all cars having same color.
Remarque 15   If x rho y, then [x]=[y].
Exemple 118   Consider the relation same as3 on N defined by xsame as3y iff 3 divides x-y.

(we also say that x and y are congruent modulo 3: xsame as y (mod 3))

What are the equivalence classes?
Définition 75   A partition of a set S is a collection of subsets { A1,...,Ak} of S such that:
  1. A1union···union Ak=S
  2. Aiintersect Aj=Ø for any i, j.
Exemple 119   Consider a set S of car, whose color are either red, blue, or green.

Define the following subsets of S:

R (red cars), B (blue cars), and G (green cars) .

Then, { R,B,G} is a partition of S.
The equivalence relation ``has the same color'' and the partition of the cars by color are closely related.
Théorème 25   In general:
  1. An equivalence relation on S defines a unique partition of S.
  2. A partition of S defines a unique equivalence relation on S.

Proof. Left as exercise:
  1. Construct the collection { A1,...,Ak}, and prove it is indeed a partition of S.
  2. Construct the relation rho, and prove it's indeed an equivalence relation.

Définition 76   Let S be a set, and rho be a relation on S.

The set of all the equivalence classes is called the quotient of S by rho.
Remarque 16   This method is used a lot in set theory:

Construction of Z from N.

Construction of Z/nZ (integers modulo n) from Z.

Construction of Q from Z.

10.4  Partially Ordered Sets


Exemple 120   What are the properties of the relation ``has to be done before'' on the tasks to build a house ?
Définition 77   A partially ordered set (or poset) is a set S with a relation rho which is
  1. Reflexive
  2. Antisymmetric
  3. Transitive
Exemple 121   Which of the following are posets ?
  1. ({1,2,3,4},<=);
  2. ({1,2,3,4},<);
  3. ({1,2,3,4},=);
  4. ({1,2,3,4},rho), with x rho y iff x divides y.
  5. (({1,2,3,4}),included in or equal to).

10.4.1  Drawing posets; Hasse diagrams


Définition 78   Some names:

Définition 79   The Hasse diagram of a poset is a drawing of this poset such that:
Exemple 122   Draw all posets on 1, 2, 3, 4 indistinct nodes.

How many such posets are there on 10 nodes ?

10.4.2  Scheduling

Scheduling a set of tasks consist in allocating tasks to resources, subject to certain constraints.
Exemple 123   Consider the house building problem, with the following assumptions:

Figure 10.1: Constraints between the tasks to build a house

Schedule the tasks between 2 workers to optimize the completion time:


  Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Day 7
Worker 1              
Worker 2              



What if there is one worker ?


  Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Day 7
Worker 1              



What if there are three workers ?


  Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Day7
Worker 1              
Worker 2              
Worker 3              


Proposition 4   Consider the problem of scheduling n tasks on p processors, subject to precedence constraints, with the same assumptions and goal as above.
This is typical from scheduling problems, where a very small change in the constraints can make huge differences in the complexity of the problems.

Also, usually the complexity is as follow: Having very good scheduling algorithms is vital in industry, because a 1% difference in completion time (for example) can save thousands of dollars. Consequently, research in this topic is well financed!

10.5  Conclusion

Chapter 11  Functions (section 4.4)

11.1  Introduction

The notion of function is pretty natural, and used in many domains (programming languages, calculus, ...). So far, the intuitive notion of function was sufficient, but we now need a more formal definition, and we will use relations for this.

We will also see how certain functions, called bijections, provide powerful counting methods.
Exemple 124   Let S be a set of cars and T be the set of all colors.

Consider the relation ``is of color''.

What properties does this relation have ?"

You can speak about THE color of the car: uniquely defined.

11.2  Formal definition of functions

11.2.1  Functions with one variable


Définition 80   A function f: S -> T between two sets S and T is a relation such that any element s of S is in relation with a unique element of T.





This unique element, denoted f(s) is the image of s.

If f(s)=y, then s is a preimage of y.


S is the domain of f;

T is the codomain of f;

The set { f(s) , sin S} is the range of f.
Exemple 125   The identity on a set S if the function idS:S-> S defined by idS(x):=x.
One way to define a function is to provide an equation, or any other mean that allows to compute the image of an element of the domain.
Exemple 126   f(n):=n+2;

f(L):=sort(L);

f(x):=[x].
Définition 81   Graph of a function from R to R (or any subset of them):
Exercice 40   Draw the graphs of the functions f(x)=x2, g(x)=(x)1/2, and h(x):=|x|.

11.2.2  Functions with several variables

The argument of a function does not need to be a simple number.
Exemple 127   f(x,y)=x2+2xy
Définition 82   A function with n variables is a function whose argument is a n-uple:
f : S1×···× Sn -> T.

Exemple 128   Here are a few functions with several variables:

11.2.3  Equality of functions


Exemple 129   Are the functions f(x):=x and g(x):=|x| equal ?

Définition 83   Two functions f and g are equal iff they have same domain S, same codomain T, and f(x)=g(x) for all x in S.

11.3  Properties of functions

11.3.1  Injective, surjective and bijective functions


Exemple 130   Let P be the set of all residents in America;

let N be the set of all assigned Social Security Number (SSN);

let SSN: P-> N be the function which assigns to each person x its SSN SSN(x).
A Social Security Number is useful because it uniquely describes a person!

That is, given an assigned SSN, you can find the person having this SSN.
Définition 84   The function SSN is invertible.

The inverse of the function SSN is the function SSN-1: N-> P such that:

SSN-1(n) is the person having n as SSN.
What properties does a function need to be invertible?

To be invertible, a function needs to have the two following properties:
Définition 85   A function f :S -> T is injective (one-to-one) iff
(for all xin S)(for all yin S) (f(x)=f(y))->(x=y)

``If x and y have the same SSN, then x is the same person as y''
Définition 86   A function f :S -> T is surjective (onto) iff
(for all yin T)(there exists xin S) f(x)=y

``For any assigned SSN, there is a person which has this SSN.''
Définition 87   A function f :S -> T is bijective iff it's injective and surjective.
Exercice 41   Which one of the following functions from R to R are bijective?
  1. f(x):=x2;
  2. f(x):=x3;
  3. f(x):=1/1+x2;
  4. f(x):=exp(x);
  5. f(x):=log(x);

11.3.2  Composition of functions


Définition 88   Let f:S-> T and g:T-> U be two functions.

The composition function g¤ f is the function from S to U defined by
g¤ f(x):=g(f(x)).

Remarque 17   The standard symbol for composition is an empty circle! In those notes a full circle is used instead due to a bug in lyx ...
Exercice 42   Define f:R->R by f(x):=x+1, and g:R->R by g(x):=x2.

What is the value of g¤ f(1)? What is g¤ f?

What is the value of f¤ g(1)? What is f¤ g?
Théorème 26   Let f:S-> T and g:T-> U be two functions.

  1. If f and g are injective, then g¤ f is injective.
  2. If f and g are surjective, then g¤ f is surjective.
  3. If f and g are bijective, then g¤ f is bijective.
Proof. 3. is a direct consequence of 1 and 2.
  1. Assume f and g are injective. We have :
    (for all x)(for all y) (f(x)=f(y)) -> (x=y)
    (for all x)(for all y) (g(x)=g(y)) -> (x=y)
    We want to prove that :
    (for all x)(for all y) (g¤ f(x)=g¤ f(y)) -> (x=y)
    Take x and y such that g¤ f(x)=g¤ f(y)
    By definition g(f(x))=g(f(y)).
    Then, since g is injective, f(x)=f(y).
    Since f is also injective x=y.
    We are done!
  2. Left as exercise.



11.3.3  Inverse of function


Exemple 131   If you take the SSN of a person, and then lookup the person having this SSN, you will get back the original person. That is, composing the function SSN and the function SSN-1 yields the identity.
Définition 89   Let f:S-> T be a function.

If there exists a function g:T-> S such that g¤ f=idS and f¤ g=idT, then g is called the inverse function of f, and is denoted f-1.
Théorème 27   A function f is bijective iff its inverse f-1 exists.
Exercice 43   Give the inverses (if they exists!) of the following functions:
  1. f(x):=x-1;
  2. f(x):=x2;
  3. f(x):=x3;
  4. f(x):=exp(x).

11.4  Functions and counting

11.4.1  Injections, surjections, bijections and cardinality of sets


Exemple 132   You distribute n different cakes between k child.

Such a distribution can be formalized by a function f:

f(4)=5 means that the 4th cake is given to the 5th child.
  1. Suppose f is injective.
  2. Suppose f is surjective.
  3. Suppose f is bijective.
Théorème 28   Let S and T be two sets.

If there exists an injective function between S and T, then |S|<=|T|.

If there exists a surjective function between S and T, then |S|>=|T|.

If there exists a bijective function between S and T, then |S|=|T|.
Note that we have never given a formal definition of the size of a set.

We just relied on the intuitive notion.

In set theory, the theorem above is actually the definition of cardinality:

11.4.2  Examples of bijections

Finite and countable sets

Do you remember how we proved that Z was countable ?

Y/B buildings, 0/1 strings and pairs of rabbits


Problem 1   Counting:
  1. buildings with yellow and blue floors, without consecutive yellow floors.
  2. strings of 0 and 1 without two consecutive 1.
The answer in both case is the Fibonacci sequence.

Those two problems are fundamentally the same:

There is a bijection between solutions of the first and solutions to the second!

So if you solve the one of them, you solve both of them.
Problem 2   Counting pairs of rabbits after n generations (ex 29 p. 140).
Here also the solution is the Fibonacci sequence.

Can you find the bijection ?

Strings of well-balanced parenthesis and Dyck paths

A string of well-balanced parenthesis is a string such as (()()), where each open parenthesis is closed and vice versa.
Définition 90   A Dyck path of size n, is a path in N×N from (0,0) to (2n,0) such that each step is either (1,1) or (1,-1).



The important fact is that such a path never goes under the x-axis.
Exercice 44   Find all strings of well-balanced parenthesis of length 0, 2, 4,6, 8, 10.

Find all Dyck paths of size 0, 1, 2, 3, 4.
Do you notice something ?
Conjecture 3   There are as many Dyck paths of size n than strings of well balanced parenthesis of length 2n.
How to prove this conjecture?

Let D be the set of Dyck paths of size n.

Let S be the set of strings of well balanced parenthesis of length 2n.

We just have to construct a bijection f:S-> D.

Take s=s1··· s2nin S, and build a path f(s) in the following way:

read s from left to right; if si is a (, go right and up, else go right and down.
Exercice 45   Draw f(s) for the following strings: (), ()(), ((()(())())()).
Why is f(s) indeed a Dyck path of size n? How to prove that f a bijection ?

Lets try to construct an inverse g for f:

Take a path p, and build a string g(p) in the following way: go through p from left two right. For each up step, add a '(' to g(p), and for each down step, add a ')'.
Exercice 46   Apply g to the paths obtained in the previous exercises.
For the same reasons as above, the resulting string g(p) is a string of well balanced parenthesis.

Moreover, by construction f(g(p))=p for any pin D and g(f(s))=s, for any sin S.

So g is indeed an inverse for f.

Therefore, f is a bijection and consequently |S|=|D|, as wanted.

Ordered trees and strings of well-balanced parenthesis


Définition 91   The set of all ordered trees can be defined recursively as follow:
Exercice 47   Draw all ordered trees on 1,2,3,4,5 nodes.
Exemple 133   Prove that any ordered tree on n nodes has n-1 edges.

Ordered trees are defined recursively, so using recursion seems reasonable.

The property is true on a tree with one node.

Let t be a tree on n>1 nodes.

Assume the property is true for any tree of size <n.

By construction, t is build by adding a common father to k trees t1,...,tk.

Let ni be the number of nodes of ti.

We have n=n1+···+nk+1.

Clearly ni<n, so by induction each ti has ni-1 edges.

Conclusion: the number of edges of t is :
(n1-1)+···+(nk-1)+k=n1+···+nk=n-1.

Théorème 29   There are as many trees with n nodes as strings of well balanced parenthesis of length 2(n-1).

Let's define recursively a bijection f between trees and well balanced parenthesis:
Exercice 48   Apply f to a few trees.
Here also, it's easy to construct the inverse of f, so f is a bijection.

Since f maps trees on n nodes on strings of length 2(n-1), and vice-versa, we are done with the proof of the theorem.

Catalan Numbers

We have seen that many different kind of objects (trees, strings of well balanced parenthesis, Dyck paths) are counted by the same sequence of numbers:
1,1,2,5,14,...

This sequence is called the Catalan sequence C(0),C(1),C(2),C(3),....
Problem 3   What is the value C(n) ?
It's enough to count, for example, the number of Dyck paths of length 2n.

There is a beautiful trick to do this. It's called André's inversion principle.

Will you find it ?

11.5  Conclusion

Part V
Modeling, Arithmetic, Computations and Languages

Chapter 12  Groups, and other algebraic structures (section 8.1)

12.1  Introduction

A mathematical structure is a formal model which capture common properties or behavior of different sets.

It consists of an abstract set, together with operations and relations which obey certain rules.

For example the set of tasks to build a house, and the set of all courses available at CSM have something in common: the notion of prerequisite. This notion can be formalized using a structure of partially ordered set.

We will introduce here certain algebraic structures, which are useful to model arithmetic, as well as to the study of symmetries.

12.2  Permutations


Définition 92   Let A be a set. A permutation of A is a bijection from A to A.

Let SA be the set of all permutations of A.

Let Sn be the set of all permutations of {1,... n}.
A permutation sigma of Sn can be written in array form as follow:
sigma:= (
(
1 2 3 4 5 6
2 1 4 5 3 6
)
)		 ,

meaning that sigma(1)=2, sigma(2)=1, sigma(3)=4, and so on.
Exercice 49   Write all permutations in S1, S2, and S3.

What is the size of Sn?

12.2.1  Operation on Sn

Sn as a set is not very interesting.

Can we define operations on Sn?
Proposition 5   The composition ¤is an operation of Sn.
Indeed, the composition of two permutations is still a permutation.

We also call this operation product of permutations.
Exercice 50   Compute the following:
(
(
1 2 3 4 5 6
2 5 1 6 3 4
)
)
-1

 
= (
1 2 3 4 5 6
)
(
(
1 2 3 4 5
5 3 4 1 2
)
)		 ¤ (
(
1 2 3 4 5
3 1 4 2 5
)
)		 = (
1 2 3 4 5
)
(
(
1 2 3 4 5
5 3 4 1 2
)
)		 ¤ (
(
1 2 3 4 5
2 3 4 5 1
)
)		 = (
1 2 3 4 5
)

(
(
1 2 3 4 5
2 3 4 5 1
)
)
5

 
= (
1 2 3 4 5
)

The permutation above produces a cycle: 1->2->3->4->5->1
Définition 93   By (a,b,c,d), we denote the permutation sigma such that sigma(a)=b, sigma(b)=c, sigma(c)=d, sigma(d)=a, and sigma(x)=x for any other element x.

Such a permutation is called a cycle.

A cycle (i,j) of length two is called a transposition.

A transposition (i,i+1) is called elementary transposition.
Exercice 51   Write (3,4,2,1) and (2,1,3,4) in array notation.

Write the following permutations in array notation:
(3,4,2,1)= (
1 2 3 4 5
)

(2,1,3,4)= (
1 2 3 4 5
)

(1,2,3)¤(4,5)= (
1 2 3 4 5 6
)

(4,5)¤(1,2,3)= (
1 2 3 4 5 6
)

(1,2,3)¤(3,4)= (
1 2 3 4 5 6
)

(3,4)¤(1,2,3)= (
1 2 3 4 5 6
)

Proposition 6   The product of two disjoint cycles is commutative.

This is not the case for non-disjoint cycles.
Exercice 52   Are the following permutations cycles?
(
(
1 2 3 4 5
5 3 4 1 2
)
)

(
(
1 2 3 4 5 6
2 1 4 5 3 6
)
)


Problem 1   So there are permutations that are not cycles.

Would it be possible to write them using only cycles?

Théorème 30   Any permutation can be written as a product of disjoint cycles.

This product is unique, up to the order.
Exercice 53   Compute the following permutations
(2,3,1,5,4)5= (
1 2 3 4 5 6
)

(
(
1 2 3 4 5 6 7 8 9 10
5 10 2 1 6 4 8 3 7 9
)
)
131

 
= (
1 2 3 4 5 6 7 8 9 10
)

Writting a permutation in cycle notation is a good way to compute powers of this permutation.

12.2.2  Generators of Sn

If you have a list, you can use a permutation to change its order.

Well, Sn is pretty big, so this makes quite a lot of possible operations.

However, some operations can be obtained by combining other operations.

Could we try to reduce the size of Sn?
Définition 94   A subset G of Sn generates Sn if any permutation can be written as a product of elements of G.
Problem 2   Find a set of generators of Sn as small as possible.

Problem 3   Does the set of all cycles generate Sn?
Problem 4   How many cycles are there ?
Can you do better?

Problem 5   Does the set of all transpositions generate Sn?

How many transpositions are there?

Can you do better?

Problem 6   Does the set of all elementary transposition generate Sn?

How many elementary transpositions are there ?

By the way, how many elementary transpositions at most do you need to express a permutation?

Can you do better than n-1 generators?

12.3  Groups

12.3.1  Definitions and examples

The notation [A,¤] denote a set A together with an operation ¤."
Problem 1   Is there anything in common between [Sn,¤] and [Z +].

Définition 95   Let A be a set with an operation ¤
What are the properties of [Z,+]? What are the properties of [R*,·]?

Those structures have many common properties.
Définition 96   [G,¤] is a group if G is a non empty set, and ¤is a binary operation on G such that:
  1. ¤ is associative
  2. an identity element exists (in G).
  3. each element of G has an inverse (in G) with respect to ¤.
If the operation ¤is commutative, G is called a commutative group.
Exercice 54   Which of the following are groups ?
  1. [Z,+]
  2. [N,+]
  3. [Z,-]
  4. [{ true,false},/\}
  5. [R,+]
  6. [R,·]
  7. [Sn,¤]
  8. [nZ,+]
What's the point ?

12.3.2  Just some examples of results and questions about groups


Théorème 31   The identity of a group is unique.

The inverse of an element is unique.

The equations a¤ x=b and x¤ a=b have a unique solution.

The inverse of a product can be computed by (x¤ y)-1=y-1¤ x-1.
Définition 97   Let [G,¤] be a group, and Aincluded in or equal to G.

Then [A,¤] is a subgroup of [G,¤] if [A,¤] itself is a group.
Théorème 32   The size of a subgroup divides the size of the group.
Problem 2   Common problems about a group:
For playing with groups, there is a very nice program:

http://www-history.mcs.st-and.ac.uk/~gap/

12.3.3  Groups and Symmetries

One common use of groups if for the study of problems with symmetries.
Exemple 134   Computing the temperature in a house with a heater in the middle.
Most of the time, a problem with symmetry has a symmetric solution.

Using this can save a LOT of time.

Problem: finding the orbits

The set of all symmetries is a group, so group theory can help you.

12.3.4  Groups and isomorphy of graph


Définition 98   The two following structures are labelled graphs:

If you exchange the nodes 3 and 4 of the first graph, you get the second.

The group Sn acts on graphs on n nodes.

Structurally, except for the numbering, there is no difference between them:

They are isomorphic.
Problem 3   Testing if two graphs are isomorphic.
This is an important but very difficult problem.
Définition 99   The following structure is an unlabelled graph:





It can be defined as an equivalence class of labelled graphs.
Problem 4   How many labelled graphs on n nodes ?

How many unlabelled graphs on n nodes ?
Group theory provides a tool (Pólya enumeration) for this.

12.4  Conclusion

References

[1]
Judith L. Gersting. Mathematical Structures for Computer Science. W. H. Freeman and Company, 4 edition, 1998.

[2]
Douglas R. Hofstadter. Gödel, Escher, Bach: an eternal golden braid. Basic Books Inc. Publishers, New York, 1979.

[3]
G. Pólya. How to solve it. Princeton University Press, Princeton, NJ, second edition, 1988. A new aspect of mathematical method.
Valid HTML 4.0! Up: Class notesClass notes Next: IntroductionIntroduction
Algebraic Structures / CSM MACS-358 / Nicolas M. Thiéry
Last modified: Fri Jan 19 13:13:02 2007