Propositional Logic
Document also available in PDF, Postscript, DVI, Text, LaTeX, LyX.

Introduction

Chapter 1 Introduction

1.1 Course Objectives

Mathematical tools for solving problems arising from computer science.

Using a computer to solve problems.

1.2 Pólya's hints for solving a problem

There are two main kinds of problems:

Problems to solve
Problems to prove

Here is a list of general questions that will guide you when you try to solve a problem.

Most of them are borrowed from ``How to solve it'' by Pólya[, p. XVI].

(*subliminal hint* you definitely should read this book!)

Whenever you get stuck and don't know what to do, browse through them, and most likely one of them will give you something to try out.

1.2.1 Phase 1: Understanding the problem

You have to understand the problem.

What is the goal ?
- What is the unknown?
- What are the data ?
- Do you need all data ? Can you simplify the data ?
What is the condition ?
- Is it possible to satisfy the condition?
- Is the condition sufficient to determine the unknown?
- Or is it insufficient? or redundant? or contradictory?
- Separate the various parts of the condition. Can you write them down?
Look at examples. Draw a figure. Introduce suitable notations.
How would you store the data on a computer ?

1.2.2 Phase 2: Devising a plan

Find the connection between the data and the unknown.

You may be obliged to consider auxiliary problems if an immediate connection cannot be found.

You should obtain eventually a plan of the solution.

Have you seen it before?
- Have you seen the same problem in a slightly different form?
- Do you know a related problem? Do you know a theorem that could be useful?
- Look at the unknown! Try to think of a familiar problem having the same or similar unknown.
Here is a problem related to yours and solved before. Could you use it?
- Could you use its result? Could you use its method?
- Should you introduce some auxiliary element in order to make its use possible?
Could you restate the problem? Could you restate it still differently?
Go back to definitions.
If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem? A more general problem? A more special problem? An analogous problem?
- Could you solve a part of the problem? Keep only a part of the condition, drop the other part. How far is the unknown then determined, how can it vary?
- Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?
Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problems?

1.2.3 Phase 3: Carrying out the plan

Carry out your plan.

Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove it is correct?

1.2.4 Phase 4: Looking back

Examine the solution obtained.

Can you check the result? Can you check the argument?
Can you derive the result differently? Can you see it at a glance?
What's the structure behind?
Can you use the result, or the method for some other problem?
Can you make it an algorithm ?
- Is your algorithm correct ?
- Can you prove it is correct ?

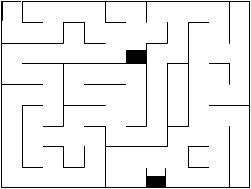
1.3 Some ``research'' about Mazes

1.4 Conclusion

The purpose of this exercise was to browse quickly through what we are going to do this semester:

1.4.1 General problem solving techniques:

We have used Pólya's list of questions as a guide to solve our problems. We will do this over and over. Usually the main difficulty with a problem is to get started. Whenever you get stuck on a problem, and don't know what to do, you should refer to this list, and see if some of the questions could give you something to try out.

1.4.2 Proofs

At some time, we had a solution for exiting from a maze. However, we were not sure if it worked all the time or not. Well, the only way to be sure that something is correct is to PROVE it.

We will need to learn how to prove things before anything else. In particular we will want to prove that certain algorithms are correct. That will be the core of our first month of class.

So what's a proof ? Basically, it's a message written by a human A to convince another human B that some fact is true (possibly A and B are the same person). When B reads through the message, he should not have any choice at the end but to say "I agree". To achieve this goal, our primary tool will be Formal Logic.

It's not easy to write good proofs. For example, a proof should be short enough that you don't get lost in the details, and detailed enough that you are sure not to have left a hole somewhere. Learning to write proofs is like learning to write. The only way is to write a lot of proofs yourself, and to take model on other's proofs. We will learn this progressively.

1.4.3 Discrete structures:

We have seen that the very structure of a maze (once we have removed all extraneous information like color, shape and so on) can be formalized with a graph, that is a set of nodes which are connected or not by edges.

A graph is a good example of discrete object, or structure (in opposition to a continuous object like a curve). We are going to see other discrete structures, and learn to recognize them when the arise at the very heart of problems. We are also going to see how to deal with such structures (algorithms and such).

1.4.4 Counting objects of a certain kind (Combinatorics)

How many mazes? how many ordered trees ?

1.4.5 Algebraic structures

That's another kind of structure that can arise in our problems. Addition, multiplication and other algebraic operations are very powerful tools. We will see that such operations can often be defined for other objects that the usual integers or real number.

1.4.6 Making a solution into an algorithm, and implementing it

Algebraic Structures

Class notes

Propositional Logic
Introduction / CSM MACS-358 / Nicolas M. Thiéry
Last modified: Fri Jan 19 13:12:14 2007