Recherche opérationnelle et Optimisation Discrète

Conclusion
Document also available in PDF, Postscript, DVI, pure text, LaTeX and LyX.

Ordonnancement

Chapitre 1 Ordonnancement

1.1 Étude de cas
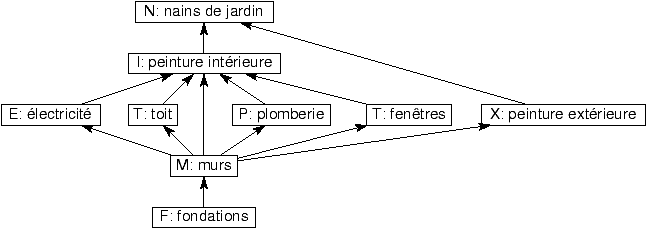
Ordonnancement de tâches avec contraintes de précédences

1.1.1 Exemple: construction d'une maison

Exercice 1 On veut construire une maison, ce qui consiste en 9 tâches, le plus rapidement possible, avec les contraintes suivantes:

Certaines tâches dépendent d'autres tâches
Toutes les tâches demandent une semaine de travail.
Chaque ouvrier ne peut travailler que sur une tâche par jour
Il n'y a pas de gain de temps si plusieurs ouvriers travaillent sur la même tâche

Exemple 1 Organisez un emploi du temps pour un ouvrier, de façon à construire la maison le plus rapidement.

	semaine 1	semaine 2	semaine 3	semaine 4	semaine 5	semaine 6	semaine 7
ouvrier 1

De même, s'il y a deux ouvriers:

	semaine 1	semaine 2	semaine 3	semaine 4	semaine 5	semaine 6	semaine 7
ouvrier 1
ouvrier 2

De même, s'il y a trois ouvriers:

	semaine 1	semaine 2	semaine 3	semaine 4	semaine 5	semaine 6	semaine7
ouvrier 1
ouvrier 2
ouvrier 3

Et s'il y a plus d'ouvriers ?

Définition 1 Dans le jargon de la recherche opérationnelle, nous avons ordonnancé des tâches (construction des fondations, ...) sur plusieurs processeurs (les ouvriers), avec des contraintes de précédences (un ordre partiel).

Un ordonnancement est optimal s'il minimise la fonction objectif (ici la durée totale).

1.1.2 Cas d'un processeur

Exercice 2 Chercher un algorithme pour ordonnancer optimalement des tâches avec contraintes de précédences sur un processeur.

Quelle est la complexité de cet algorithme?

Démontrez l'optimalité de l'ordonnancement obtenu.

En fait, ce que l'on recherche c'est une énumération t₁,...,t_n des tâches de sorte que si t_i<t_j

alors i<j. Une telle énumération des tâches est appelée extension linéaire de l'ordre partiel.

On peut voir ça comme un tri des tâches. Mais attention, on ne peut utiliser les algorithmes de tri usuels en O(nlog n), (tri insertion, tri fusion, ...), que si l'ordre est total (toutes les tâches sont comparables).

1.1.3 Cas d'un nombre illimité de processeurs

Exercice 3 Chercher un algorithme pour ordonnancer optimalement des tâches avec contraintes de précédences sur un nombre infini de processeurs.

Quelle est la complexité de cet algorithme?

Démontrez l'optimalité de l'ordonnancement obtenu.

Il s'agit d'un algorithme glouton.

À chaque étape, on maximise localement le nombre de tâches effectuées, et il se trouve que le problème est suffisamment simple pour que le résultat soit un optimal global.

1.1.4 Cas de deux processeurs

Exercice 1 Ordonnancez optimalement les trois ordres partiels suivants sur 2 processeurs:

1: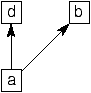

, 2:

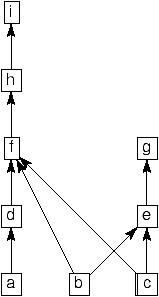, 3: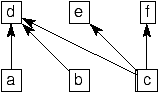

Algorithme de Coffman-Graham (algorithme de liste)

L'idée est comme pour p=oo de construire un algorithme de type glouton.

On associe à chaque tâche t une priorité P(t).

Il sera pratique de considérer un processeur inactif comme en train d'exécuter une tache vide Ø. C'est d'ailleurs pas si déraisonnable, vu que en pratique en assembleur il y a une instruction spécifique nop pour dire à un processeur de ne rien faire.

Par convention, on pose P(Ø)=-oo.

Algorithme 1.1.1 Algorithme de liste pour ordonnancer des tâches unitaires soumises à des contraintes de précédences sur p processeurs.

Calculer la priorité P(t) de toutes les tâches.
d:=1.
Parmi les tâches minimales (on dira aussi disponibles), en choisir p de priorité maximale (s'il y a moins de p tâches minimales, les prendre toutes), et les placer dans l'ordonnancement à la date d.

Le choix du processeur est sans importance; par convention, on mettra celle de poids max sur le premier processeur, et ainsi de suite.

On note t_d,k la tâche exécutée au temps d sur le processeur k.
Réitérer à la date d:=d+1 avec les tâches restantes.

On appelle cet algorithme algorithme de liste parce qu'une façon de l'implanter est de commencer par construire une liste des tâches par ordre de priorité décroissantes, et ensuite de construire l'ordonnancement en prenant les éléments dans la liste dans l'ordre.

Exercice 4 Trouver des fonctions de priorité pour que cet algorithme de liste donne des ordonnancements optimaux dans les cas p=1 et p=oo.

Il s'agit essentiellement d'une généralisation des algorithmes que l'on a vu précédemment.

Exercice 5 Évaluez la complexité de cet algorithme.

Exercice 6 Peut-on avoir t_d,1=Ø ?

Seulement si on est arrivé à la fin de l'ordonnancement.

Remarque 1 la priorité P(t_d,1) des tâches sur le premier processeur est décroissante.

Exercice 7 Vérifiez-le!

Donnez aussi un contre-exemple dans le cas du deuxième processeur.

Soit t une tâche placée à une date >d. En regardant successivement les prédécesseurs de t de date >d, on fini par trouver une tâche t'<= t disponible. D'après le critère de choix de la tâche sur le premier processeur, on a P(t')<= P(t_d,1). Comme la fonction de priorité est croissante, on en déduit que P(t)<= P(t_d,1).

Contre exemple: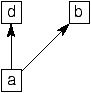

Problème 1 Quelle fonction de priorité choisir dans le cas de deux processeurs ?

P(t):=nombre de successeurs de t:

Avec l'ordre 2 ci-dessus, l'algorithme donne un ordonnancement non optimal.
P(t):=taille de la plus grande chaîne partant de t:

Avec l'ordre 3 ci-dessus, l'algorithme donne de manière non-déterministe un ordonnancement non optimal.

Définition 2 On va définir P(t) récursivement comme suit:

Pour chaque tâche t maximale, on pose P(t):=0.

On regarde ensuite les tâches maximales dans le reste de l'ordre.

Pour chacune d'entre elles, on construit la liste décroissante des priorités de ses successeurs immédiats. Pour déterminer quelles sont les tâches les plus prioritaires, on compare ces listes lexicographiquement. Ensuite, on assigne aux tâches les priorités 1, 2, ... par ordre de priorité.

On réitère avec les tâches restantes.

Exercice 8 Calculer les priorités pour les ordres ci-dessus, ainsi que l'ordonnancement correspondant.

Donner un exemple sur lequel le calcul des priorités est intéressant.

Évaluer la complexité du calcul des priorités.

Théorème 1 L'algorithme de Coffman-Graham donne un ordonnancement optimal.

La preuve du théorème repose sur le lemme suivant.

Lemme 1 Soit d telle que P(t_d,2)<P(t) pour une certaine tâche t exécutée après t_d,2 (typiquement, t_d,2=Ø). Alors, t_d,1<t. La construction de la fonction de priorité nous permet de dire bien plus fort: pour toute tâche vérifiant P(t')>= P(t_d,1), on a t'<t.

Exercice 9 Démontrez le! Indication: on considèrera d'une part l'ensemble T des tâches t exécutées après t_d,2, et d'autre part l'ensemble T' des tâches t' telles que P(t')>= P(t_d,1).

Proof: Principe de la preuve du théorème.

On pose d₀:=0, et on repère les positions d₁, d₂,... comme ci-dessus.

On définit des blocs de tâches B₀, B₁, B₂,... entre chacune de ces positions:

B_k:=

{
{

d_k+1,1

d_k+1,2

,...,t

d_k+1,1

}
}

En appliquant le lemme, on montre que toutes les tâches de B₀ précèdent toutes les tâches de B₁, et ainsi de suite avec les blocs suivants.

Cette décomposition en blocs prouve l'optimalité de l'ordonnancement. QED

Exercice 10 Donnez les décompositions en blocs de la preuve dans les exemples d'ordonnancements que l'on a vu.

Algorithme de Fuji et al.

Cet autre algorithme est basé sur la remarque suivante:

Remarque 2 Un ordonnancement de tâches de durée unitaire sur 2 processeurs est une couverture de l'ordre partiel an antichaînes de taille au plus 2, de sorte que deux antichaînes ne se croisent pas.

Algorithme 1.1.2 Ordonnancement de tâches unitaires soumises à des contraintes de précédences sur 2 processeurs.

Chercher une couverture de l'ordre partiel en antichaînes de taille au plus 2.
(Comment peut-on faire ça ?)
Décroiser les antichaînes obtenues.

Le faire sur un exemple intéressant

1.1.5 Cas de p processeurs

Problème 2 Est-ce que l'algorithme de Fuji et al. marche encore ?

Indication: analysez l'exemple suivant sur 3 processeurs:

Conclusion: la couverture optimale en antichaînes de taille au plus 3 est composée de deux antichaînes; mais on ne peut pas les décroiser en un ordonnancement de durée 2.

Problème 3 Est-ce que l'algorithme de Coffman-Graham marche encore ?

Indication: analysez les exemples suivants sur 3 processeurs:

Conclusion: Coffman-Graham sur 3 processeurs donne un ordonnancement raisonnable, mais pas forcément optimal.

Problème 4 Peut-on quand même utiliser un algorithme de liste pour trouver une solution optimale?

Comment chercher toutes les solutions optimales?

Définition 3 Un ordonnancement sera dit tassé à gauche s'il n'y a pas de date d avec un processeur inactif, alors qu'il restait des tâches disponibles. Les algorithmes de liste donnent de tels ordonnancements tassés à gauche.

Exercice 11 Montrer que tout ordonnancement O peut être transformé en un ordonnancement O' tassé à gauche sans augmentation de durée totale.

En déduire qu'il existe toujours un ordonnancement tassé à gauche optimal.

On dit que l'ensemble des ordonnancements tassés à gauche est dominant.

Montrez que tout ordonnancement tassé à gauche peut être obtenu par un algorithme de liste (indication: construire une fonction de priorité ad hoc pour cet ordonnancement).

On peut en fait utiliser le principe des l'algorithmes de liste pour faire une recherche exhaustive:

À chaque fois que l'on doit faire un choix de p tâches parmi les tâches disponibles, on explore à tour de rôle tous les choix possibles. On parcourt alors un arbre de choix, dont les extrémités sont les ordonnancements tassés à gauches.

C'est ce qu'on appelle un méthode arborescente.

Évidement, la complexité devient exponentielle!

Pour limiter les dégâts, il faut autant que possible essayer d'éliminer les choix qui sont clairement mauvais, de façon à couper des branches.

Typiquement, si on a déjà trouvé un ordonnancement de durée D, ce n'est pas la peine d'explorer les branches où les choix déjà faits impose qu'il y ait des tâches après D.

Une telle méthode s'appelle branch and bound en anglais.

Cas particulier: l'ordre de précédence est une anti-arborescence

Théorème 2 Si l'ordre de précédence est une anti-arborescence, alors l'algorithme de liste avec comme fonction de priorité la cohauteur donne un ordonnancement optimal.

1.1.6 Ordonnancement de tâches de durées non unitaires

Problème 5 Parmi les algorithmes que nous avons vu précédemment, lesquels s'adaptent au cas ou les tâches sont de durées arbitraires ?

Cas d'un processeur

Exercice 12 Est-ce qu'un algorithme de liste donne un ordonnancement optimal ?

Pas de difficulté: n'importe quelle extension linéaire de l'ordre des tâches fera l'affaire.

Cas d'un nombre illimité de processeurs

Exercice 13 Est-ce qu'un algorithme de liste donne un ordonnancement optimal ?

Pas de difficulté.

Il s'agit en fait d'un cas particulier de la méthode PERT: pour déterminer la durée totale, il suffit de rechercher un chemin critique. C'est encore un cas de théorème min-max, qui peut être vu comme cas particulier du théorème de dualité de la programmation linéaire.

Exercice 14 Déterminer la complexité de la recherche d'un chemin critique.

D'ailleurs on peut aussi utiliser la programmation linéaire, comme on l'avait fait en TP.

Tel quel, c'est un peu utiliser un marteau pilon!

Mais on avait pu de la sorte traiter des variantes de ce problème, avec par exemple des tâches de durées variables, moyennant un coût, etc.

Cas de deux processeurs

Théorème 3 Même sans contrainte de précédences, le problème d'ordonnancer des tâches sur 2 processeurs de manière optimale est NP-complet!

1.1.7 Synthèse

On a vu ici des exemples d'applications des principales méthodes d'ordonnancement:

Méthode PERT
Méthodes de liste
Programmation linéaire
Méthodes arborescentes avec stratégies de coupes

Proposition 1 Considérons le problème d'assigner n tâches de durées unitaires sur p processeurs, sous des contraintes de précédences, et avec les contraintes et but comme ci-dessus.

1 ou 2 processeurs: algorithmes en O(n+m);
3 processeurs: complexité inconnue;
p processeurs: NP-complet
oo processeurs: O(n+m).

Ceci est typique des problèmes d'optimisation discrète, où de légères modifications dans les contraintes peuvent faire une grande différence de complexité. En fait, la complexité évolue souvent de la manière suivante:

Pas de contrainte: facile
Quelques contraintes: complexité polynomiale de degré de plus en plus grand
Plus de contraintes: très difficiles (NP-complet). Les algorithmes sont basés sur une recherche arborescente.
Encore plus de contraintes: facile. Éventuellement toujours NP-complet, mais la plupart des branches peuvent être coupées très tôt, ce qui donne une bonne complexité en moyenne.

1.2 Description des problèmes d'ordonnancements

De manière générale, un problème d'ordonnancement consiste à organiser l'exécution de tâches, en leur attribuant des ressources et en fixant leurs dates d'exécution. Pour une classification des différents types d'ordonnancements, nous renvoyons à l'introduction de [Carlier_Chretienne.PO].

Notation 1.2.1 Quelques notations relativement standard (que l'on a pas forcément respecté ci-dessus!):

m: nombre de machines;
n: nombre de tâches;
I: ensemble des tâches;
i: indice d'une tâche ou d'un événement;
t_i: date de début d'exécution de la tâche i ou de l'événement i;
C_i: date de fin d'exécution de la tâche i;
C_max: durée totale de l'ordonnancement: C_max:=max(C_i);
p_i: durée de la tâche i;
p_i,j: durée de la tâche (i,j) (graphe CPM/PERT)
p_ik: durée de la tâche i sur la machine k;
r_i: date de disponibilité de la tâche i;
d_i: date échue de la tâche i (dead-line);
T_i: retard de la tâche i: T_i:=max(0,C_i-d_i);
U_i: indice de retard: U_i=1 si la tâche est en retard, et 0 sinon;
w_i: poids de la tâche i;
a_ij: contrainte potentielle entre deux tâches (t_j-t_i>= a_ij);
<: ordre partiel sur l'ensemble des tâches.

Exercice 15 Ci-dessous est une liste de problèmes (pour la plupart déjà rencontrés dans ce cours), et qui rentrent dans le cadre des problèmes d'ordonnancements. Déterminer la classification de chacun de ces problèmes, ainsi que la valeur des différentes variables ci-dessus. Précisez aussi quelles sont les contraintes disjonctives et les contraintes cummulatives.

Ordonnancement de tâches unitaires sur des processeurs avec contraintes de précédences;
Assignement de cours à des professeurs (ou de nageurs pour un relais 4 nages);
Problème des visites;
Conception d'un emploi du temps dans un petit collège. Pour simplifier, on suppose que toutes les classes, de la 6ème à la 3ème, ont le même nombre d'heures de chaque matière, et qu'il y a un professeur par matière;
Ordonnancement du chantier du TP.

1.3 Méthodes polynomiales et pseudo-polynomiales

Nous allons voir une série de cas particuliers pour lesquels il existent des méthodes polynomiales de résolution.

Il faudrait être prudent avec la définition de polynomial.

Polynomial en quoi ? Polynomial en la taille des données.

Or, dans les données des entiers peuvent apparaître, et il y a deux façons de mesurer la taille d'un tel entier a:

Le nombre de bits pour stocker a en base 2, c'est-à-dire log(a).
Le nombre de bits pour stocker a en base 1, c'est-à-dire a.

Selon le choix de cette mesure, le même algorithme peut être polynomial ou exponentiel.

Un algorithme est polynomial s'il est polynomial pour la mesure 1.

Un algorithme est pseudo-polynomial s'il est polynomial pour la mesure 2.

Nous renvoyons à [Carlier_Chretienne.PO, p. 76]pour les détails.

1.3.1 Ordonnancement de tâches morcelables (avec préemption)

Lorsque les tâches sont morcelables, les problèmes deviennent nettement plus faciles, et on peut plus souvent les résoudre par des méthodes polynomiales ou pseudo-polynomiales.

Machines identiques / intervalles de temps distincts

Problème 6 Le but est d'ordonnancer des tâches morcelables de durée p₁,...,p_n sur m machines identiques de telle sorte que la tâche i s'exécute dans l'intervalle de temps [r_i, d_i].

Exercice 16 Ordonnancement sur deux machines identiques, de quatre tâches morcelables A,B,C,D avec p_A=p_B=p_D=2, p_C=4; d_A=d_D=5; d_B=3, d_C=4; r_A,r_B,r_C=0, r_D=2.

Construisez un problème de transport permettant de résoudre ce problème par la programmation linéaire.

Indice: découper le temps en 5 plages horaires [0,1], [1,2], [2,3], [3,4], [4,5].

Remarque 3 Cette méthode ne marche que si les dates r_i et d_i sont entières!

De plus, on ne s'autorise à morceler les tâches qu'en fragments de durée entière. Il est concevable qu'un morcellement plus fin puisse donner de meilleurs résultats.

Si l'on accepte ces restrictions, la programmation linéaire donne un algorithme pseudo-polynomial (le nombre de plage horaires est borné par max(d_i)-min(r_i)).

Exercice 17 Pour le moment on a seulement cherché une solution faisable du problème d'ordonnancement. Cela peut se faire efficacement par un algorithme de flot.

On veut maintenant en plus optimiser la date de fin d'exécution. Construisez un problème de transport qui permette de résoudre ce problème.

Indice: Introduisez des coûts sur le réseau précédent.

Machines identiques / durée minimale

Problème 7 Le but est d'ordonnancer des tâches morcelables de durée p₁,...,p_n sur m machines identiques en minimisant la durée totale C_max.

Exercice 18 Donner un ordonnancement optimal pour m:=3, n:=5, p₁:=10, p₂:=8, p₃:=4, p₄:=14, p₅:=1.

Exercice 19 On pose

B:=max

(
(
(
(
(
(
(

max_i p_i,

(
(
(
(
(
(
(

--
\
/
--

i=1

p_i

)
)
)
)
)
)
)

Vérifiez que B<= C_max.

On peut construire facilement un ordonnancement vérifiant B=C_max (et donc optimal)!

Il suffit de remplir le diagramme de Gantt de gauche à droite et de haut en bas.

Exemple 2 Ordonnancement de Mac Naughton pour m:=3, n:=5, p₁:=10, p₂:=8, p₃:=4, p₄:=14, p₅:=1.

La définition de B assure que les tâches ne se recouvrent pas elles-mêmes (p_i<= B), et qu'il y a assez de place (sum_i=1ⁿp_i<= mB). Il se trouve que cela suffit!

Algorithme 1.3.1 (Mac Naughton)

B:=max (max_i p_i, 1/m(sum_i=1ⁿp_i)).
t:=0; k:=1;
Pour chaque tâche i:
1. Si t+p_i<= B, on affecte i sur la machine k entre les instants t et t+p_i et on pose t:=t+p_i.
2. Sinon on affecte i sur la machine k entre t et B et sur la machine k+1 entre les instants 0 et p_i-(B-t), et on pose k:=k+1 et t:=p_i-(B-t).

Exercice 20 Construire un ordonnancement pour m:=4 et (p₁,...,p₇):=(5,10,2,8,3,4,20).

On remarque qu'il y a a relativement peu de préemptions (au plus m-1).

Machines identiques, temps minimal, contraintes de précédences

Problème 8 Le but est d'ordonnancer des tâches morcelables de durée p₁,...,p_n sur m machines identiques en minimisant la durée totale C_max, et avec des contraintes de précédences entre les tâches.

Exercice 21 Donnez des algorithmes polynomiaux pour une et deux machines, et pour un nombre illimité de machines.

Dans ces trois cas, on peut se ramener au problème d'ordonnancement de tâches unitaires en morcelant chaque tâche i en une succession de p_i tâches unitaires.

Remarque 4 Il faut tout de même supposer que les durées des tâches sont entières.

Pour être précis, les algorithmes ainsi obtenus sont pseudo-polynomiaux.

Machines distinctes, temps minimal

Problème 9 Le but est d'ordonnancer des tâches morcelables sur machines distinctes en minimisant la durée totale C_max, sachant que la durée d'exécution de la tâche i sur la machine j est p_ij.

Exercice 22 Le tableau suivant donne les valeurs de p_ij pour 4 tâches devant être exécutées sur 3 machines. Donnez un encadrement rapide de C_max.

tâchemachine	1	2	3
1	15	10	6
2	9	9	9
3	8	6	8
4	3	3	2

Slowinski et Labetoulle et Lawler ont proposé une méthode très esthétique pour résoudre ce problème via la programmation linéaire.

L'idée est de ne pas se préoccuper, dans un premier temps, des dates exactes à laquelle les tâches seront exécutées. On ne s'intéresse qu'à la durée totale x_ij que la tâche i passe sur la machine j dans un ordonnancement donné. Une deuxième phase, le théorème de Birkhoff-Von Neumann (si si!) permettra de construire les détails de l'ordonnancement.

Exercice 23 Vérifiez que pour tout ordonnancement, les x_ij sont solution faisable du programme linéaire suivant:

--
\
/
--

j=1

x_ij<= C_max, pour i=1,...,n

--
\
/
--

i=1

x_ij<= C_max, pour j=1,...,m

--
\
/
--

j=1

x_ij

p_ij

=1, pour i=1,...,n

x_ij>=0, pour i=1,...,n et j=1,...,m

où l'on minimise C_max.

La première phase consiste à chercher une solution x_ij optimale pour ce programme linéaire.

Exercice 24 Une solution optimale de ce programme linéaire pour notre exemple est donnée par la table suivante. On a C_max:=9.

Construisez un ordonnancement de durée C_max donnant ces valeurs aux x_ij.

tâchemachine	1	2	3
1			6
2	3	3	3
3	4	3
4	2	1

A-t'on été chanceux?

Il n'est pas évident qu'il existe toujours un ordonnancement optimal de durée C_max!

Exemple 3 Construction systématique pour notre exemple.

Pour construire un tel ordonnancement, on transforme la matrice des x_ij en une matrice M bistochastique en rajoutant une ligne et une colonne avec des coefficients c_i et l_j idoines:

c_i:=C_max-sum_j=1^mx_ij :durée totale pendant laquelle la tâche i n'est pas exécutée;
l_j:=C_max-sum_i=1ⁿx_ij :durée totale pendant laquelle la machine j ne fait rien.

Pour être précis, c'est 1/C_maxM qui est une matrice bistochastique.

Le théorème de Birkhoff-Von Neumann permet alors de décomposer M sous la forme

--
\
/
--

k=1

lambda_kP_k,

où chaque P_k est une matrice de permutation et sum_klambda_k=C_max.

On construit l'emploi du temps final en associant à chaque k une plage de temps de durée lambda_k pendant laquelle les tâches sont assignées aux machines selon la permutation P_k!

1.3.2 Ordonnancement de tâches non morcelables

Problème central de l'ordonnancement; modélisation par graphe potentiel tâche

Rappel: soit i et j deux tâches d'un problème d'ordonnancement, et t_i et t_j leurs dates respectives de début d'exécution. On appelle contrainte potentielle une containte de la forme t_j-t_i>= a_ij.

Exercice 25 Considérons un ensemble de cinq tâches {1,2,3,4,5} soumises aux contraintes temporelles suivantes:

La tâche i dure p_i;
La tâche 2 commence au temps 3;
Les tâches 2 et 3 doivent se chevaucher sur au moins une unité de temps;
La tâche 4 ne peut commencer qu'après la fin des tâches 1 et 2;
La tâche 5 ne peut pas commencer avant le début de la tâche 3.

Il n'y a pas de contraintes de ressources.

L'objectif est d'optimiser la durée totale.

Modéliser ces contraintes par des contraintes potentielles. On rajoutera deux tâches fictives 0 et 6 de façon à mesurer facilement la durée totale par t₆-t₀.

Représenter ces contraintes sur un graphe dont les sommets sont les tâches et les arêtes sont les contraintes.

Peut-on éliminer certaines arêtes ?

Quelles méthodes pour traiter ce problème ?

Définition 4 Le problème central de l'ordonnancement consiste à choisir les dates d'exécutions pour un ensemble de tâches I, de façon à respecter des contraintes potentielles et à minimiser la durée totale.

Le graphe utilisé ci-dessus s'appelle graphe potentiel-tâche.

Il s'agit d'une variante des graphes potentiel-événement utilisés à l'origine dans les méthodes CPM/PERT. Les graphes potentiel-tâches ont l'avantage d'être souvent plus simples, et de permettre plus facilement l'introduction de nouvelles contraintes.

Exercice 26 Peut-on modéliser par un graphe potentiel tâche:

Des contraintes de précédences ?
Des dates de disponibilité? Des dates échues ?
Des délais de communication ?
Des durées d'exécution ?
Des contraintes de ressources ?

Les problèmes avec contraintes de ressources (contraintes disjonctives/cumulatives) sont habituellement beaucoup plus difficiles que ceux sans (problèmes de décision), et ne peuvent pas être modélisés par des graphes potentiel-tâches. Une approche classique est de les modéliser par des réseaux de Pétri temporisés. Nous renvoyons à [Carlier_Chretienne.PO] pour plus d'information.

1.3.3 Problèmes sans contraintes de ressources

Optimisation de la durée totale

Exercice 27 Donner une méthode polynomiale pour résoudre un problème modélisé par un graphe potentiel-tâche, et pour lequel on veut optimiser la durée totale.

Étude de faisabilité

Exercice 28 Le problème modélisé par le graphe potentiel tâche suivant a-t'il une solution ?

Définition 5 La valeur d'un chemin dans le graphe potentiel-tâches est la somme des coefficients sur les arcs du chemin.

Si le graphe potentiel-tâche a un cycle de valeur strictement positive, alors il n'y a pas de solutions. En fait, il s'agit du seul cas ou il n'y ait pas de solutions:

Théorème 4 Il existe une solution faisable si et seulement si le graphe potentiel-tâche n'a pas de cycles de valeur strictement positive.

En particulier, s'il les valuations sont strictement positives, il n'y a de solution que s'il n'y a pas de cycles. C'est typiquement le cas pour des contraintes de précédences.

Exercice 29 On a déjà démontré l'un des sens du théorème. L'objectif de cet exercice est de donner un démonstration constructive de l'autre sens.

On suppose qu'il n'y a pas de cycles de valeur strictement positive, et on veut démontrer qu'il y a une solution faisable.

Soit i et j deux tâches, et C_ij l'ensemble des chemins élémentaires (sans boucles) allant de i à j. Vérifier que C_ij est fini.

Si C_ij est vide, on pose l(i,j):=-oo. Sinon, il existe donc un chemin dans C_ij de plus grande valeur; un tel chemin est appelé critique, et on note l(i,j) sa valeur. Vérifier que si c est un chemin quelconque allant de i à j, alors sa valeur est inférieure à l(i,j).

On défini pour chaque tâche i, sa date d'exécution au plus tôt r_i:=l(0,i).

Vérifiez que les r_i ainsi définis forment une solution faisable.

Vérifiez qu'il s'agit aussi d'une solution optimale pour la durée totale.

Problème 10 Comment calculer les r_i effectivement ?

Lorsqu'il n'y a pas de cycles, il suffit de faire un parcours en profondeur du graphe, en partant du sommet 0 (algorithme en O(m), où m est le nombre de contraintes).

Dans le cas général, les potentiels t_i peuvent être interprétés comme les variables duales du problème de transport construit à partir du graphe potentiel-tâches. Du coup, les r_i peuvent être calculés par une variante de l'algorithme de Ford-Fulkerson en O(n³) (en gros, comme dans la démonstration du théorème, on peut se contente de chercher une solution faisable; celle-ci sera directement optimale si on s'y prend bien; donc on est ramené à un problème de flot).

Potentiels calés à gauche et à droite

On appelle les r_i ensemble de potentiels calés à gauche. On pourrait de même construire un ensemble de potentiels calés à droite, en partant cette fois de la dernière tâche. On obtient alors les dates d'exécution au plus tard

f_i:=l(0,n+1)-l(i,n+1).

Pour tout ordonnancement optimal, on a alors r_i<= t_i<= f_i (pourquoi ?).

La quantité f_i-r_i mesure combien de marge on a pour exécuter la tâche i.

Lorsque i est sur un chemin critique, on a f_i-r_i=0: si on perds du temps dans l'exécution de la tâche i la durée totale de l'ordonnancement sera affectée.

Dans l'ensemble des tâches pour préparer un cours, la photocopie des documents est clairement une tâche critique ...

Ce que l'on vient de faire est une méthode de chemin critique. C'est une variante de la méthode CPM/PERT, ou méthode des potentiels (cf. [Carlier_Chretienne.PO, p. 112])

Optimisation d'une fonction linéaire des t_i

Remarque 1.3.2 Ce que l'on vient de faire se généralise lorsque l'on recherche non plus à optimiser la durée totale t_n+1-t₀ de l'ordonancement, mais une fonction linéaire quelconque des t_i. On peut toujours se ramener à un programme linéaire, et en fait même à un problème de transport (mais plus forcément à un problème de flot).

Exercice 2 Regarder comment cette remarque s'applique pour le problème du chantier que l'on avait vu en TP.

1.3.4 Problèmes avec contraintes de ressources renouvellables

La plupart de ces problèmes sont NP-complets, même dans des cas apparemment simple comme l'ordonnancement sur deux processeurs de tâches indépendantes, mais de durées quelconques.

Il y a quelques exceptions comme celles que l'on avait rencontré au début:

Tâches unitaires sur 1 et 2 processeurs identiques avec contraintes de précédences
Tâches unitaires indépendantes avec contraintes de disponibilité ou de dates échues

1.3.5 Problèmes à ressources consommables

Exercice 30 Lire [Carlier_Chretienne.PO, p. 101-107].

En particulier calculer un ordonnancement optimal pour l'exemple p. 104.

1.4 Méthodes Arborescentes et dynamiques

1.5 Algorithmes approchés

Références

[Carlier_Chretienne.PO]: Problèmes d'ordonnancement, Modélisation, Complexité, Algorithmes; J. Carlier, P. Chrétienne, Masson, Études et recherches en informatique, 1988.

Programmation Linéaire

Recherche opérationnelle et Optimisation Discrète

Conclusion
Ordonnancement / UCBL, Maîtrise MIM, Recherche Opérationnelle / Nicolas M. Thiéry
Last modified: Fri Jun 25 12:06:36 2004

Ordonnancement

Chapitre 1 Ordonnancement

1.1 Étude de casOrdonnancement de tâches avec contraintes de précédences

1.1.1 Exemple: construction d'une maison

1.1.2 Cas d'un processeur

1.1.3 Cas d'un nombre illimité de processeurs

1.1.4 Cas de deux processeurs

Algorithme de Coffman-Graham (algorithme de liste)

Algorithme de Fuji et al.

1.1.5 Cas de p processeurs

Cas particulier: l'ordre de précédence est une anti-arborescence

1.1.6 Ordonnancement de tâches de durées non unitaires

Cas d'un processeur

Cas d'un nombre illimité de processeurs

Cas de deux processeurs

1.1.7 Synthèse

1.2 Description des problèmes d'ordonnancements

1.3 Méthodes polynomiales et pseudo-polynomiales

1.3.1 Ordonnancement de tâches morcelables (avec préemption)

Machines identiques / intervalles de temps distincts

Machines identiques / durée minimale

Machines identiques, temps minimal, contraintes de précédences

Machines distinctes, temps minimal

1.3.2 Ordonnancement de tâches non morcelables

Problème central de l'ordonnancement; modélisation par graphe potentiel tâche

1.3.3 Problèmes sans contraintes de ressources

Optimisation de la durée totale

Étude de faisabilité

Potentiels calés à gauche et à droite

Optimisation d'une fonction linéaire des ti

1.3.4 Problèmes avec contraintes de ressources renouvellables

1.3.5 Problèmes à ressources consommables

1.4 Méthodes Arborescentes et dynamiques

1.5 Algorithmes approchés

Références

1.1 Étude de cas
Ordonnancement de tâches avec contraintes de précédences

Optimisation d'une fonction linéaire des t_i