Plus courts chemins, avec poids: l”algorithme de Dijkstra

On considère le graphe suivant qui modélise un réseau routier :

%load_ext autoreload
%autoreload 2
from graph import examples
from dijkstra import *
G = examples.dijkstra()
G.show()

On souhaite calculer le plus court chemin entre deux sommets de ce graphe.

Exercice

1. Complétez la fonction dijkstra du fichier dijkstra.py.

2. Appliquez cette fonction au graphe G ci-dessus:

# VOTRE CODE ICI
raise NotImplementedError()

Exercice, suite

3. Déduisez en la distance entre A et J, à mettre dans la variable distance_AJ:

# VOTRE CODE ICI
raise NotImplementedError()

# Vérifie votre résultat sans dévoiler la solution, par la magie des fonctions de hachage :-)
import hashlib
assert hashlib.md5(bytes(distance_AJ)).hexdigest() == '2f6064003b888e403627e493532fc751'

distances = dijkstra(G, "A")[0]
assert distances["A"] == 0

assert sum(distances.values()) == 2774

Exercice, suite

4. Implantez la fonction shortest_path dans dijkstra.py, et utilisez là pour calculer un plus court chemin entre A et J dans G:

# VOTRE CODE ICI
raise NotImplementedError()

Exercice, suite

5. Pour aller plus loin : Instrumentez votre fonction pour en visualiser l’exécution.

# VOTRE CODE ICI
raise NotImplementedError()

Problème 1: le trajet le plus rapide en métro de Montgallet à Billancourt ?

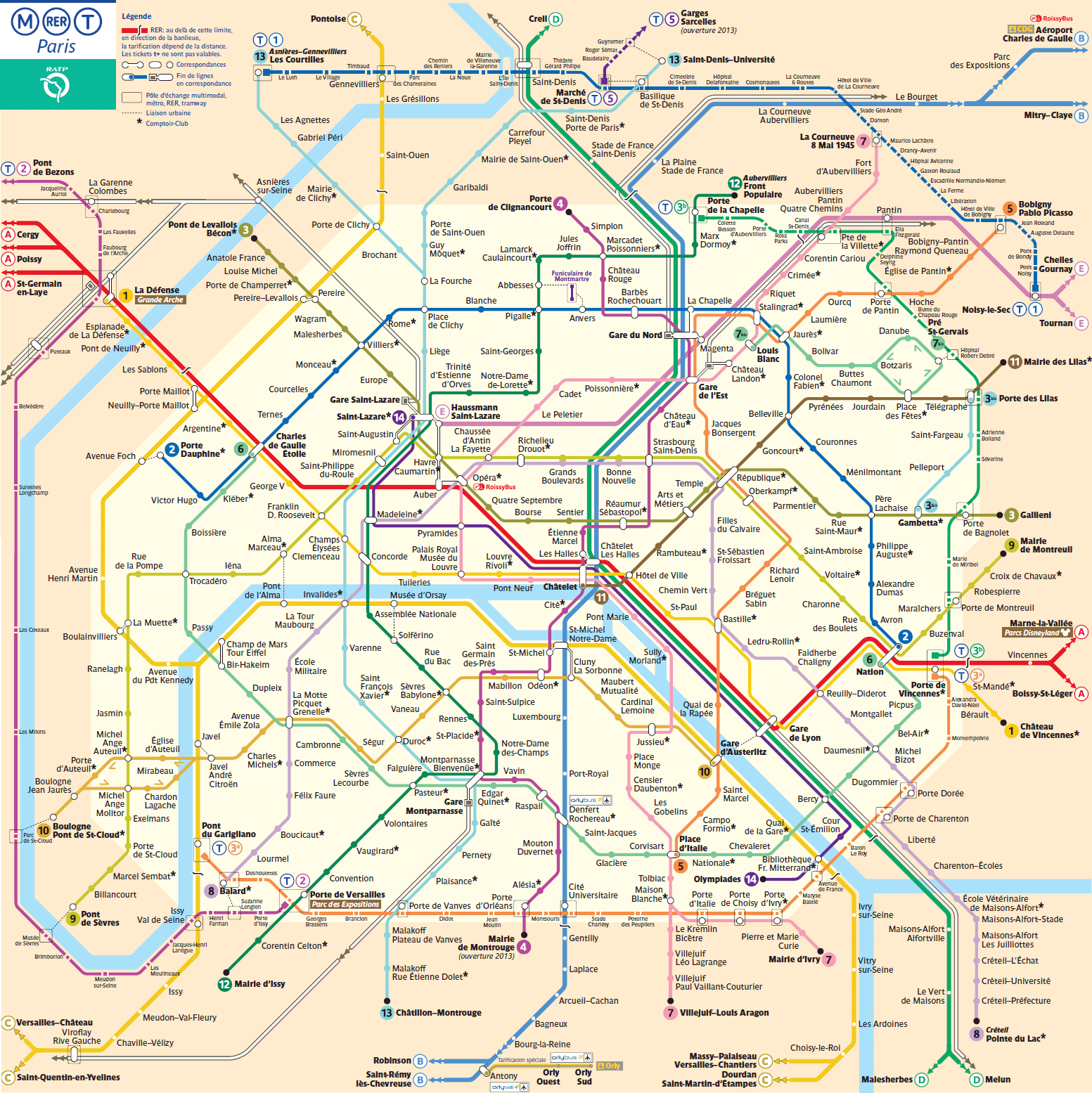
1. Le fichier metro_complet.txt contient la description d’un graphe modélisant le métro de Paris. Consultez son contenu pour en comprendre le format.

2. Implantez une fonction qui lit le fichier et renvoie le graphe qu’il contient sous la forme d’un objet de type Graph.

3. Utilisez la fonction dijkstra pour calculer un plus court chemin de Montgallet à Billancourt! Vous stockerez la longueur de ce chemin dans dans la variable distance.

# VOTRE CODE ICI
raise NotImplementedError()

# VOTRE CODE ICI
raise NotImplementedError()

# Vérifie votre résultat sans dévoiler la solution, par la magie des fonctions de hachage :-)
import hashlib
assert hashlib.md5(bytes(int(distance))).hexdigest() == '47699f4b69b37670eb6ce45276ad9a30'