Algorithme de Kruskal#
Idée : On part du graphe \(T=(V, \emptyset)\) et on ajoute tour à tour une nouvelle arête de plus petit poids qui ne crée pas de cycles (i.e. qui connecte deux composantes connexes différentes).
Invariant : À l’étape \(i\), le graphe \(T\) est acyclique avec \(i\) arêtes de poids minimal
Dans ce qui suit nous exécutons à la main, l’algorithme de Kruskal
from graph import Graph, examples
import networkx
import matplotlib
import matplotlib.pyplot as plt
## On part d'un graphe valué et on fixe un dessin
G = examples.cours_1_reseau()
GNX = G.networkx()
layout = networkx.planar_layout(GNX)
edges_weight = {(u, v) : w for u, v, w in G.edges()}
## On visulise la progression de l'algorithme en affectant à chaque arête un état représenté par une couleur
from enum import Enum, unique
@unique
class Status(Enum):
AFAIRE = 0
GARDEE = 1
SUPRIMEE = 2
ENCOURS = 3
colors_code = {
Status.AFAIRE : 'black',
Status.GARDEE : 'green',
Status.SUPRIMEE : 'lightgray',
Status.ENCOURS : 'red'
}
def show_kruskal(status):
plt.figure()
colors = [colors_code[status[u,v]] for (u, v) in GNX.edges()]
networkx.draw(GNX, layout, edge_color = colors, width=3, linewidths=1,
node_size=500, node_color = 'lightgray', alpha=0.9,
labels = {node : node for node in G.vertices()})
networkx.draw_networkx_edge_labels(GNX, layout, edge_labels= edges_weight, font_color='black')
plt.axis('off')
plt.show()
# Au début toutes les arêtes sont marquée "à faire"
edges_status = {(u, v) : Status.AFAIRE for u, v, _ in G.edges()}
show_kruskal(edges_status)
# On choisit l'une des arêtes de poids minimum
edges_status["F", "G"] = Status.ENCOURS
show_kruskal(edges_status)
# Elle ne crée pas de cycle. On la garde
edges_status["F", "G"] = Status.GARDEE
show_kruskal(edges_status)
# On choisit l'une des arêtes de poids minimum
edges_status["B", "C"] = Status.ENCOURS
show_kruskal(edges_status)
# Elle ne crée pas de cycle. On la garde
edges_status["B", "C"] = Status.GARDEE
show_kruskal(edges_status)
# L'algorithme se continue ainsi
edges_status["B", "G"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["B", "G"] = Status.GARDEE
edges_status["A", "G"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["A", "G"] = Status.GARDEE
edges_status["C", "H"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["C", "H"] = Status.GARDEE
edges_status["E", "G"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["E", "G"] = Status.GARDEE
show_kruskal(edges_status)
# On Passe maintenant aux arêtes de poids 3
edges_status["E", "F"] = Status.ENCOURS
show_kruskal(edges_status)
# L'arête E - F crée un Cycle, on la supprime
edges_status["E", "F"] = Status.SUPRIMEE
show_kruskal(edges_status)
# On Passe maintenant a A - B
edges_status["A", "B"] = Status.ENCOURS
show_kruskal(edges_status)
# L'arête A - B crée un Cycle, on la supprime
edges_status["A", "B"] = Status.SUPRIMEE
show_kruskal(edges_status)
# Idem pour E - H
edges_status["E", "H"] = Status.SUPRIMEE
show_kruskal(edges_status)
# L'algorithme se poursuit
edges_status["A", "F"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["A", "F"] = Status.SUPRIMEE
edges_status["C", "D"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["C", "D"] = Status.GARDEE
edges_status["G", "H"] = Status.ENCOURS
show_kruskal(edges_status)
edges_status["G", "H"] = Status.SUPRIMEE
show_kruskal(edges_status)
# On pourrait continuer jusqu'à ce que l'on ai vu toutes les arêtes...
# On remarque que l'on a choisi 7 arêtes dans un graphe à 8 sommets. On peut donc s'arrêter dès maintenant.
edges_status["C", "G"] = Status.SUPRIMEE
edges_status["D", "E"] = Status.SUPRIMEE
edges_status["D", "H"] = Status.SUPRIMEE
show_kruskal(edges_status)
On a calculé un arbre couvrant de poids 13 du graphe.
L’invariant de l’algorithme est le suivant:
À chaque étape, le graphe des arêtes choisies est un graphe partiel acyclique de \(G\) de poids minimum
Exercice 2. Appliquer à la main l’algorithme de Kruskal au deux graphes suivants. On donnera un arbre couvrant de poids minimal et un arbre couvrant de poids maximal. Pour ce dernier on applique le même algorithme mais en choissant un arête de plus fort poids.
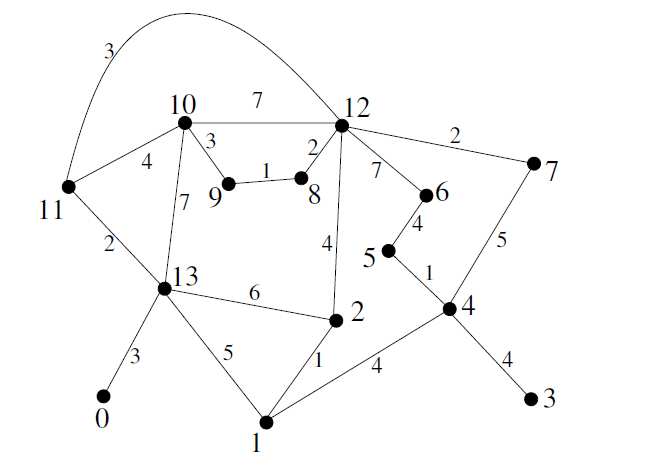
Donner le poids de l’arbre couvrant obtenu.
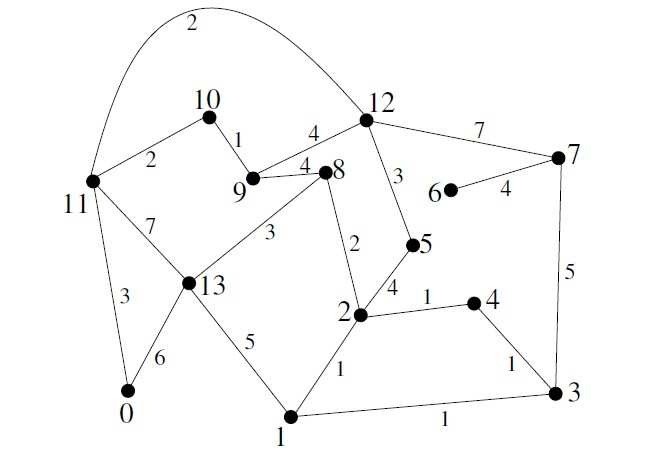
Donner le poids de l’arbre couvrant obtenu.
Expliquer pourquoi l’invariant est conservé.
Stucture de donnée “Union-Find”#
Dans l’algorithme de Kruskal, on a besoin de savoir en permanence si les deux extrémités de l’arête considérée sont dans la même composante connexe. Il serait très inefficace de refaire à chaque fois un parcours. On a donc besoin d’une structure de donnée qui permet de maintenir les composantes connexes du graphe partiel au cours de l’algorithme. C’est la structure Union Find.
C’est une structure de données qui représente une partition d’un ensemble fini. On rappelle qu’une partition d’un ensemble \(E\) est un ensemble de parties non vides de \(E\) deux à deux disjointes et dont l’union est \(E\). Dans notre application la partition est l’ensemble des composantes connexes de \(V\).
L’idée d’union find est de choisir dans chaque composante connexe un sommet dit « canonique ». On va ensuite implémenter les deux méthodes suivantes:
find(v): quel est le sommet canonique de la composante connexe d’un sommet \(v\) donné.union(u, v): mettre à jour la structure de donnée pour réunir les composantes des sommets canoniques \(u\) et \(v\).
Pour ceci, on va stocker une forêt où chaque arbre est un chaînage d’une composante connexe qui pointe vers le sommet canonique.
Dans une telle forêt, le représentant de chaque classe est la racine de l’arbre correspondant. Find se contente de suivre les liens vers les nœuds pères jusqu’à atteindre la racine. Union réunit deux arbres en attachant la racine de l’un à la racine de l’autre.
Vous pouvez trouver des détail sur Union-Find.
Il existe une applet de simulation.
À Faire#
Écrire une classe UnionFind implémentant les trois méthodes suivantes:
UnionFind(S): constructeur (__init__en Python) qui initialize l’ensemble avec toutes les classes singletonsUF.find(i): trouve l’élément canonique de la classe deiUF.union(i, j): réuni les classes associées àietj
On utilisera les deux optimisations:
heuristique du rang pour diminuer la hauteur de l’arbre en cas d”
Union.compression des chemins dans le cas d’un find : on reparcourt le chemin en associant directement le noeud canonique aux éĺéments du chemin. On écrira une version itérative.
Tester UnionFind
La classe UnionFind permet d’avoir un autre algorithme pour calculer les composantes connexes :
on part de la partition triviale (tous les sommets sont seuls dans leur classes)
on appelle
union(i,j)pour toutes les arêtes \(i - j\).
À la fin, on obtient la partition des sommets en composantes connexes.
Ecrire une méthode connected_componentsUF() et vérifier sur tous les graphes d’exemple qu’elle renvoie le même résultat que connected_components()
En utilisant UnionFind, écrire l’algorithme de Kruskal pour calculer l’arbre couvrant de poids minimum d’un graphe.
Tester votre fonction sur les graphes du fichier graph_exemples.py
Application : Construction d’un labyrinthe#
En partant du graphe grille \(m*n\), construire un labyrinthe parfait à l’aide d’un arbre couvrant. On pourra faire un affichage ASCII comme ci-dessous.
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | | | | | | | | |
+ + +---+ + + + + +---+ +---+ +---+---+ + + + +---+ +
| | | | | | | | | | | | | |
+ +---+ + +---+ +---+ +---+---+---+ +---+ + + +---+ + + +
| | | | | | | | | | | |
+ + +---+ + +---+ +---+ +---+---+ + +---+---+---+ +---+ +---+
| | | | | | | | | | | |
+ + +---+ +---+ +---+ + +---+---+---+ + + + +---+ +---+ +
| | | | | | | | | | | |
+---+---+---+---+---+ +---+ +---+---+---+ +---+---+ + + + + + +
| | | | | |
+---+ +---+---+ + +---+---+ +---+ +---+---+---+ + +---+---+---+---+
| | | | | | | | | | |
+---+---+ +---+ + + + +---+---+ +---+---+---+ + +---+ +---+ +
| | | | | | | | | |
+ +---+ +---+ +---+ +---+---+---+---+---+ +---+---+ +---+---+ + +
| | | | | | | | | | | | | |
+ + + +---+ + + + + +---+---+ +---+ +---+---+ + +---+ +
| | | | | | | | |
+ +---+---+ + +---+ +---+ +---+ + +---+---+ +---+---+---+ +---+
| | | | | | | | | |
+---+---+ +---+ +---+ +---+---+---+---+---+---+ +---+ + +---+---+ +
| | | | | | | | | | |
+---+ + +---+ + + +---+ + + + +---+ +---+ + +---+ + +
| | | | | | | | | | |
+---+ + + +---+ + + + +---+---+---+ + + +---+---+---+---+---+
| | | | | | | | | | | | | |
+ + +---+ +---+ +---+ + +---+---+ + + + + +---+ + +---+
| | | | | | | | | | | |
+---+ +---+---+---+---+---+ +---+ + + +---+ +---+ + + + + +
| | | | | | | | | | |
+ +---+ +---+ +---+---+---+---+---+---+ +---+---+ +---+ + +---+---+
| | | | | | | | | |
+---+---+ + +---+ + + +---+ + +---+ +---+ + +---+ + + +
| | | | | | | | | | | |
+---+---+ + + + +---+ + +---+ +---+---+---+ +---+ +---+ + +
| | | | | | | | | | |
+ +---+ +---+---+ + +---+ +---+ +---+---+ + + + +---+ +---+
| | | | | | | | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
