Les cycles d’un graphe

Contenu

Les cycles d’un graphe#

Motivation : routage dans un réseau#

https://en.wikipedia.org/wiki/Spanning_Tree_Protocol

« broadcast » : un noeud quelconque du réseau émet une information qui doit être retransmise à tous les noeuds du réseau

N’est possible que si le graphe est connexe !

Proposition d’algorithme :

Chaque noeud qui reçoit l’information la retransmet à ses voisins sauf à celui duquel il l’a reçu.

Problème : Si il y a un cycle dans le réseau, l’information va tourner indéfiniment le long du cycle. En réalité, la situation est même bien pire car certain noeud du réseau vont dupliquer l’information ( »broadcast storm »).

Définition formelle#

Définition : Un cycle d’un graphe $G = (V, E)$ est une liste $C = (c_0, \dots, c_{k-1})$ de sommets telle que

$k > 2$ : on interdit en particulier les allez-retours
les $c_i$ sont distincts
pour tout $i$ entier, $(c_i, c_{i+1})$ est une arrête de $G$ où $i$ est compris modulo $k$ (c’est-à-dire que $(c_{k-1}, c_0)$ est aussi une arête)

Note : Dans le cas des graphes orienté, la notion de cycle ne tient pas compte du sens des arêtes. Si l’on suit toujours les arêtes dans leurs sens, on parle de circuit.

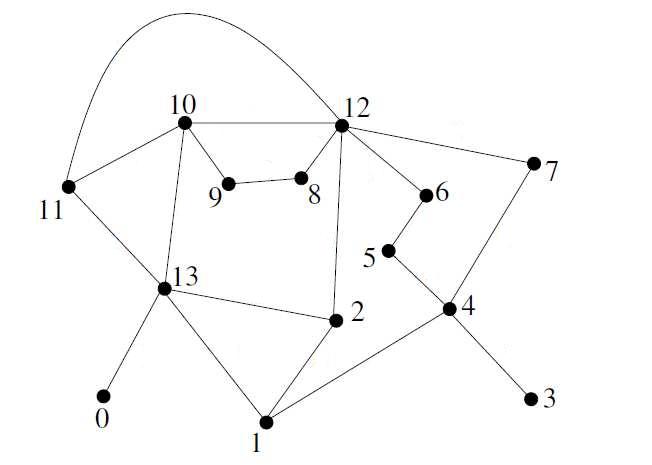
Exemple de cycles dans le graphe précédent: $(1, 2, 13)$ et $(4, 7, 12, 2, 1)$.

Contre-exemple de cycle :

$(11, 10, 12, 8, 9, 10, 13)$ : passe deux fois par le noeud $10$;
$(11, 12, 7)$ : $7 - 11$ n’est pas une arête.

À faire:

remplacer le ficher graph.py par le votre après y avoir copier et coller la partie suivant le commentaire

# Partie sur les cycles dans un graphe à copier dans votre solution
Implanter et tester la méthode is_cycle

Note : pour toutes les méthodes à compléter, on pourra toujours les écrire dans le notebook sous la forme d’une fonction avant de les mettre dans la classe graphe.

Problème de la recherche de cycles dans un graphe#

Questions étant donné un graphe $G$:

le chemin $s$ est-il un cycle de G ? Méthode G.is_cycle(s)
$G$ a-t-il un cycle ? Méthode G.is_acyclic()
touver un cycle de $G$: Méthode G.find_cycle()

Note : il n’est pas forcément nécessaire de trouver un cycle pour savoir qu’un graphe contient un cycle.

Lemme fondamental des cycles dans un graphe#

Lemme 1 : Soit $G$ un graphe (simple, non orienté). Soient $u, v$ deux sommets de $G$ tel que $u - v$ n’est pas une arête de $G$. Soit $G'$ le graphe ontenu en ajoutant $u-v$ à $G$. Alors, de deux choses l’une :

soit $u$ et $v$ sont dans la même composante connexe de $G$, et il y a un cycle dans $G'$ de la forme $(u, \dots, v)$;
soit $u$ et $v$ ne sont pas dans la même composante connexe de $G$ et alors $G'$ possège une composante connexe de moins que $G$.

À faire : justifier le lemme précédent

Nombre d’arcs dans un graphe et cycles#

Proposition 2 : Soit $G = (V;E)$ un graphe. Alors:

Si $G$ est connexe, alors $|E| \geq |V| - 1$.
Si $G$ est sans cycle, alors $|E|\leq |V| - 1$.

Preuve : On va partir du graphe $(V, \emptyset)$ et l’on va rajouter une à une les arêtes de $G$. On remarque qu’au départ le nombre de composantes connexes est $|V|$ et qu’il y aura $|E|$ étapes où l’on rajoute une arête.

Comme à chaque étape le nombre de composantes connexes diminue au plus de $1$, il faut au moins $|V| - 1$ étapes pour que le graphe devienne connexe (une composante connexe).
Quand on a créé un cycle, rajouter des arêtes en plus le conserve. Si à la fin $G$ est sans cycles, on a donc jamais créé de cycles. Le nombre de composant connexe a donc diminué exactement de $1$ à chaque étape.

Dans la preuve du point 2, on a en fait prouvé le résultat plus fort suivant:

Proposition 3 : Un graphe $G=(V;E)$ est sans cycle si et seulement si $$|V| = k + |E|$$ où $k$ est le nombre de composantes connexes.

Algorithme is_acyclic(G) : on fait un parcours de graphe pour compter les composantes connexes

Implanter les méthodes suivantes dans la classe Graphe:

connected_components
is_connected
is_acyclic

Pour chacune des méthodes, on donnera ci-dessous où dans le code la complexité dans le cas le pire.

Algorithme find_cycle(G) : on fait un parcours en profondeur de graphe en partant d’un noeud et en notant pour chaque noeuds traversés comment on l’a atteint. Si l’on atteint deux fois un noeuds, on a trouvé un cycle.

Implanter la méthode find_cycle(G) et donner sa complexité.

Notion d’arbre#

Définition : Un arbre est un graphe connexe et sans cycle (on dit aussi acyclique)

Dans un arbre, on a pas de problème pour le routage:

Proposition 4. $G$ est un arbre si et seulement si, pour tout couple de sommets $s$ et $t$, il existe un unique chemin simple (qui ne repasse jamais deux fois par le même sommet) de $s$ à $t$.

Proposition 5. (Caractérisations d’un Arbre) : Pour un graphe $T$ à $n$ sommets, il y a équivalence entre les propriétés :

$T$ est un arbre

$T$ est un graphe connexe à $n-1$ arêtes
$T$ est acyclique à $n-1$ arêtes
$T$ est connexe, et la suppression de toute arête le déconnecte
$T$ est acyclique et l’ajout de toute arête le rend cyclique.

Preuve :

$1.\Rightarrow 2.$ et $1.\Rightarrow 3.$ sont des conséquence immédiate de la proposition 2
$2.\Rightarrow 1.$ et $3.\Rightarrow 1.$ sont des conséquence de la proposition 3.

À faire : justifier ci-dessous les équivalences des points 4. et 5.

Implanter la méthode G.is_tree() et donner sa complexité.