Codes correcteurs

Codes correcteurs#

\(\newcommand{\ZZ}{\mathbb{Z}}\newcommand{\NN}{\mathbb{N}}\)

Quelques Références:

Introduction#

Objectif du codage#

Un expéditeur Alice transmet un message \(m\) à Bob sur un canal bruité.

Problématique

  • Comment Bob peut-il détecter l’existence d’erreurs de transmission

  • Comment Bob peut-il corriger des erreurs éventuelles

Note

Contrairement à la cryptographie, la problématique n’est pas de se protéger d’un tiers malicieux, mais d’un bruit aléatoire.

Exemples d’applications#

  1. NASA/CNES/…: communication avec des sondes et satellites

  2. CD / DVD

  3. Transfert de données par Internet (TCP, CRC, MD5 checksum)

  4. Téléphones portables

Quelles sont les contraintes spécifiques à chacune de ces applications?

Premiers exemples de codes#

Langages humains!#

Syntaxe: orthographe, grammaire, lexique

Anglais: \(500000\) mots de longueur moyenne \(10\) sur en gros \(26^{10}\), soit une proportion de \(10^{-9}\).

Exemple: pomme, abrucot, poime (pomme, poire, prime, poème)

Sémantique: sens, contexte, …

Exemple: codage de parité sur 7 bits#

Alice veut envoyer le message \(m = 0100101\)

Elle le code en un mot à 8 bit avec un nombre pair de 1, en rajoutant un bit de parité: \(c = 01001011\)

Le code est transmis \(c\) et éventuellement altéré.

Bob reçoit \(c'\) et regarde s’il y a un nombre pair de 1.

  • Si non, comme pour \(c' = 01101011\), \(B\) détecte qu’il y a eu erreur

  • Si oui comme pour \(c' = 10001011\), \(B\) suppose que \(c=c'\)

Premiers concepts#

Définitions

Un code \(C\) est un sous-ensemble de mots dans \(M:=A^{n}\), où

  • \(A\) est un alphabet, comme \(A:=\ZZ/q\ZZ= \{0,1,...,q-1\}\) .
    Typiquement \(q=2\) (codes binaires).

  • \(n\) est un entier, la dimension du code

Codage: on transforme le message envoyé \(m\) en un mot \(c\) du code.

Transmission: en passant à travers le canal, \(c\) devient \(c'\).

Détection d’erreur: on essaye de déterminer si \(c=c'\); approximation: on teste si \(c'\) est dans \(C\)

Correction d’erreur: on essaye de retrouver \(c\) à partir de \(c'\).

Décodage: on retrouve le message \(m\) à partir de \(c\).

Décodage par distance de Hamming#

Définition

Distance de Hamming entre deux mots: nombre de lettres qui diffèrent (en comparant lettre à lettre).

Stratégie:

  1. Détection d’erreur: est-ce que \(c'\) est dans le code \(C\)?

  2. Correction d’erreur par distance minimale: on renvoie le mot de \(C\) le plus proche de \(c'\).

Exercice: Est-ce raisonnable?

On suppose que lors de la transmission chaque lettre a une probabilité \(p\) d’être corrompue, indépendemment des autres.

Calculer la probabilité qu’un mot de longueur \(n\) arrive intact? Avec une erreur au plus? Avec deux erreurs au plus?

Application numérique:

n = 7; p = 0.1
(1-p)^n

(1-p)^n + n*p*(1-p)^(n-1)

(1-p)^n + n*p*(1-p)^(n-1) + binomial(n,2) * p^2*(1-p)^(n-2)

n = 7; p = 0.01
(1-p)^(n-1)

(1-p)^n + n*p*(1-p)^(n-1)

(1-p)^n + n*p*(1-p)^(n-1) + binomial(n,2) * p^2*(1-p)^(n-2)

Définitions

  • Capacité de détection: \(D(C)\) nombre maximal d’erreurs que l’on est sûr de détecter

  • Capacité de correction: \(e(C)\) nombre maximal d’erreurs que l’on est sûr de corriger

  • Distance \(d(C)\) du code: distance minimale entre deux points distincts du code

Formalisation#

Pour formaliser cela, il est pratique d’introduire la notion de boule naturellement associée à une métrique: étant donné \(x\in M\) et un entier \(k\geq 0\), la boule de centre \(x\) et de rayon \(k\) est:

\[B(x,k) = \{y\in M,\quad d(x,y) \leq k\}\]

Alors:

\[D(C) := \max_{k\in \mathbb{N}\cup\{\infty\}} \quad \forall c\in C, \quad B(c,k) \cap C = \{c\}\]
\[e(C) := \max_{k\in \mathbb{N}\cup\{\infty\}} \quad \forall c_1\, c_2\in C, \quad B(c_1,k) \cap B(c_2,k) \ne \emptyset \Longrightarrow c_1=c_2\]
\[d(C) := \min_{x\ne y\in C} d(x,y)\]

Cas dégénérés#

Lorsque \(|C|\leq 1\), on prendra par convention \(d(C)=+\infty\). Cela peut paraître plus naturel en prenant la définition alternative:

\[d(C) := \max_{k\in \mathbb{N}\cup\{\infty\}} \forall x\ne y \in C, \quad k\leq d(x,y)\]

Exercice: en petite dimension

On fixe \(A=\ZZ/2\ZZ\) (codes binaires).

  1. Trouver tous les codes de \(M=A^n\) pour \(n=1\), \(n=2\), \(n=0\).

  2. Pour chacun d’entre eux, donner la distance \(d(C)\), la capacité de détection \(D(C)\), la capacité de correction \(e(C)\). Dessiner les boules de centres dans \(C\) et de rayon \(e(C)\).

  3. Permettent-t’ils de corriger une erreur?

  4. Donner un code de \(M=A^3\) permettant de corriger une erreur.

  5. Peut-on faire mieux?

Proposition

Capacité de détection: \(D(C) = d(C) - 1\).

Capacité de correction: \(e(C) = \llcorner\frac{d(C)-1}2\lrcorner\).

Borne de Hamming, codes parfaits#

Conjecture de Kepler

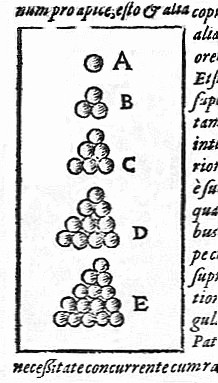
Problème: Kepler discret

On se fixe un alphabet \(A\) avec \(q=|A|\), une dimension \(n\) et une capacité de correction \(e\). Combien de mot peut on coder au maximum?

De manière équivalente: combien de boules non intersectantes de rayon \(e\) peut-on faire rentrer dans \(M\)?

Exemples: visualisation des boules de rayon \(e\) autour de quelques codes binaires

Chargement de quelques fonctions, et configuration des plots 3D:

%run "codes_correcteurs.py"
from sage.plot.plot3d.base import SHOW_DEFAULTS
SHOW_DEFAULTS['frame'] = False
SHOW_DEFAULTS['aspect_ratio'] = [1,1,1]
SHOW_DEFAULTS['viewer'] = 'threejs'

Les boules dans \(M=A^3\) pour \(A=\mathbb{Z}/q\mathbb{Z}\):

@interact
def _(r=slider(0,3,1), q=slider(2,7,1)):
    A = IntegerModRing(q)
    M = A^3
    return dessin_boules([M.zero()], r)

Le code binaire de triple répétition:

A = GF(2)
M = A^3
C = M.subspace([[1,1,1]])
C.list()

dessin_boules(C,1)

et sur \(A=\mathbb{Z}/3\mathbb{Z}\):

A = GF(3)
M = A^3
M.list()[:9]

C = M.subspace([[1,1,1]])
C.list()

dessin_boules(C,1)

Le code de Hamming:

A = GF(2)
M = A^7
C = codes.HammingCode(A, 3)
C.cardinality()

dessin_boules(C, 1, projection=projection_7_3)

Exercice: Borne de Hamming sur \(|C|\).

Soit \(A=\mathbb{Z}/q\mathbb{Z}\).

  1. Taille de la boule \(B(x,e):=\{y,\quad d(x,y)\leq e\}\) de \(A^n\) de centre \(x\) et de rayon \(e\)? Indication: commencer par \(q=2\) et \(x=0\cdots0\).

  2. Taille de \(A^n\)?

  3. Conclusion?

Solution

\[|B(x,e(C))| = \sum_{k=0}^{e(C)} \binom n k (q-1)^k \qquad \qquad |C||B(x,e)| \quad \leq \quad q^n\]

Application numérique:

@interact
def _(q=slider(1,7,default=2), n=slider(0,10, default=3), e=slider(0,10,default=1)):
    m = q^n
    b = sum(binomial(n,k)*(q-1)^k for k in range(0, e+1))
    print(f"|M|={m}, |B(x,e(C))|={b}, |C|≤ {1.0*m/b:.2}")

Définition: code parfait

Un code \(C\) est parfait si on a égalité: \(|C| |B(x,e(C))| = |A^n|\), i.e.

\[|C| \sum_{k=0}^{e(C)} \binom n k (q-1)^k \quad = \quad q^n\]

Exemples

Dans tous les exemples vus jusqu’ici, les seuls codes parfaits sont les codes triviaux, le code de triple répétition sur un alphabet à deux lettres et le code de Hamming.

Problème

Algorithmes de codage? de décodage?

Codes linéaires#

Principe: on rajoute de la structure pour rendre les algorithmes plus efficaces.

Définition

Un code linéaire est un sous-espace vectoriel de \(A^n\), où \(A\) est un corps fini.

Commençons par un petit échauffement.

Exercice: algèbre linéaire sur \(A=\mathbb{Z}/2\mathbb{Z}\), à la main

Soit \(H\) la matrice:

A = GF(2); A

H = matrix(A, [[0,1,1,1, 1,0,0],
               [1,0,1,1, 0,1,0],
               [1,1,0,1, 0,0,1]]); H

  1. Appliquez le pivot de gauss à \(H\).

  2. Est-ce que les vecteurs \((1,1,0,0,1,1,0)\) et \((1,0,1,1,1,0,1)\) sont dans le sous-espace vectoriel engendré par les lignes de \(H\)?

  3. Conclusion?

Solution:

H[1], H[0] = H[0], H[1]
H

H[2] = H[2] + H[0]

H

H[2] = H[2] + H[1]
H

H[0] = H[0] + H[2]
H[1] = H[1] + H[2]
H

u = vector(A, (1,1,0,0,1,1,0))
v = vector(A, (1,0,1,1,1,0,1))

Question: est-ce que \(u\) est dans le sous-espace vectoriel engendré par les lignes de \(H\)?

On cherche \(a,b,c\) tels que \(u = a H[0] + b H[1] + c H[2]\)

u

u = u - H[0]
u

u = u - H[1]
u

Donc \(u\) est dans le sous-espace engendré par les lignes de \(H\)

v

v = v - H[0]
v

v = v - H[2]
v

Donc \(v\) n’est pas dans ce sous-espace

Exemples#

Exemple: bit de parité

Sept bits plus un huitième bit dit de parité tel que le nombre total de bit à \(1\) est pair.

v: mon mot

\(v_0 + v_1 + v_2 + v_3 + v_4 + ... + v_7=0\) sssi le nombre de bit à est pair

Exemple: code de Hamming \(H(7,4)\).

Quatre bits \(\left(a_{1},a_{2},a_{3},a_{4}\right)\) plus trois bits de redondance \(\left(a_{5},a_{6},a_{7}\right)\) définis par:

\[\begin{split}\begin{aligned} a_{5} = a_{2}+a_{3}+a_{4}\\ a_{6} = a_{1}+a_{3}+a_{4}\\ a_{7} = a_{1}+a_{2}+a_{4} \end{aligned}\end{split}\]

Algorithmes#

Comment tester si un mot appartient au code?#

Avec Sage:

A = GF(2); A

n = 7
M = A^7; M

Matrice de contrôle:

H = matrix(A, [[0,1,1,1, 1,0,0],
               [1,0,1,1, 0,1,0],
               [1,1,0,1, 0,0,1]])

Test d’appartenance au code:

mot_du_code = M([1,0,1,1,0,1,0]);
H * mot_du_code

mot_quelconque = M([1,1,0,1,0,1,1]);
H * mot_quelconque

Refaites le à la main!

Le code lui-même est le noyau de \(H\):

C = H.right_kernel()
C

mot_du_code in C

mot_quelconque in C

Refaites le à la main!

Est-ce que l’on pourrait trouver \(C\) encore plus rapidement?

Oui:

MatrixSpace(A,4,4)(1).augment(H[:,0:4].transpose())

Exercice:#

  • Combien y-a-t’il de mots dans le code de Hamming \(C=H(7,4)\)?

  • Calculer la distance de ce code (indice: se ramener en zéro!)

  • Quelle est sa capacité de détection? de correction? Est-il parfait?

Solution:

C.cardinality()

def poids(c): return len([i for i in c if i])

poids(M([0,1,0,0,0,0,0]))

poids(M([1,0,1,1,0,1,0]))

min(poids(m) for m in C if m)

Comment coder un message en un mot du code?#

Matrice génératrice:

G = C.matrix(); G

M = A^4
m = M([1,0,1,0])
c = m * G; c

Comment décoder un mot du code en un message?#

Du fait de la forme de la matrice génératrice:

G

le mot du code c est simplement obtenu en ajoutant des bits supplémentaires à la fin du mot original. C’est une propriété souhaitable des codes correcteurs car elle permet de bien séparer information originale et information redondante. En particulier, décoder est trivial: il suffit de récupérer les quatre premiers bits.

Exemples: la clé de contrôle de votre numéro de sécurité sociale.

Correction d’erreur par syndrome#

Exercice

  1. Partir du mot zéro, le coder, et faire alternativement une erreur sur chacun des bits. Noter le résultat après multiplication par la matrice de contrôle.

  2. Prendre un mot à 4 bits de votre choix, le coder, faire une erreur sur un des 7 bits, corriger et décoder. Vérifier le résultat.

  3. Que se passe-t’il s’il y a deux erreurs?

Soit \(c\) dans le code: alors \(H c = 0\)

Après transmission, on obtient \(c' = c + 𝜖\), où \(𝜖\) est l’erreur.

Alors: \(Hc' = H (c + 𝜖) = Hc + H𝜖 = H𝜖\)

On voit \(𝜖\) comme une maladie et \(𝜖\) comme un syndrome de la maladie: ce que l’on vient de calculer, c’est que deux malades ayant la même maladie auront le même syndrome. La réciproque est vraie tant que \(𝜖\) reste dans la capacité de correction (prouvez le!).

Cela nous donne la stratégie du décodage par syndrome suivante:

  • Précalculer tous les syndromes \(H𝜖\) pour toutes les «maladies» \(𝜖\) dans la capacité de correction, et en faire une table.

  • Pour corriger \(c'\), on calcule son syndrôme \(Hc'\). S’il est nul, \(c'\) est déjà dans le code: \(c=c'\). Sinon on retrouve dans la table \(𝜖\) tel que \(Hc'=H𝜖\), et on corrige \(c'\) par \(c=c'-𝜖\).

Codes cycliques#

Principe: encore plus de structure pour être encore plus efficace.

Définition

Un code \(C\) est cyclique s’il est stable par rotation des mots:

\[1010010\in C \Longleftrightarrow 0101001\in C \Longleftrightarrow 1010100\in C \Longleftrightarrow \cdots\]

Les praticiens ont noté que les codes cycliques avaient de bonnes propriétés.

Donnons une structure d’anneau quotient à \(M=A^n\) en l’identifiant avec \(A[X]/(X^n-1)\).

Sous cette identification, les mots ci-dessus correspondent à

\[1 + X^2 + X^5, X+X^3+X^6, 1+X^2+X^4\]

Remarque

Dans \(A[X]/(X^n-1)\), décalage = multiplication par \(X\).

Par exemple, pour \(A[X]/(X^7-1)\):

\[\begin{split}\begin{aligned} X(1+X^2+X^5) = X + X^3 + X^6\\ X(X + X^3 + X^6) = X^2+X^4+X^7 = 1+X^2+X^4 \end{aligned}\end{split}\]

Codes cycliques \(\longleftrightarrow\) idéaux dans \(A[X]/(X^n-1)\).

Soit \(g\) un diviseur de \(X^n-1\), et \(h\) tel que \(gh=X^n-1\).

  • Code: idéal engendré par \(g\)

  • Codage: \(m\mapsto mg\)

  • Détection d’erreur: \(c*h=0\)

  • Décodage: division par \(g\) modulo \(X^n-1\) (par ex. par Euclide étendu)

Codes BCH

On peut construire des codes cycliques de capacité de correction déterminée à l’avance. Pour en savoir plus, voir Wikipedia, Codes BCH.

Codage par interpolation (Reed-Solomon)#

Exercice (secret partagé)

Un vieux pirate est sur son lit de mort. Dans sa jeunesse il a enfoui un Fabuleux Trésor dans la lagune de l’Ile de la Tortue, quelque part à l’est du Grand Cocotier. Il a réuni ses dix lieutenants préférés pour leur transmettre l’information secrète indispensable: la distance entre le Grand Cocotier et le Trésor. Connaissant bien ses lieutenants, et dans un étonnant dernier sursaut de justice, il ne voudrait pas qu’une conjuration de quelques uns d’entre eux assassine les autres pour empocher seuls le trésor. En tenant cependant compte de la mortalité habituelle du milieu, il souhaite donner une information secrète à chacun de ses lieutenants pour que huit quelconques d’entre eux puissent retrouver ensemble le trésor, mais pas moins. Comment peut-il s’y prendre?

Application aux CD/DVD: Codage CIRC

Paramètres du système de codage:

  • un corps fini \(GF(q)\).

  • trois entiers \(k\), \(d\), et \(l\) avec \(d\leq l\)

  • \(l\) points d’évaluation \(x_1,\ldots,x_l\) dans \(GF(q)\)

  • un procédé D de codage sur \(GF(q)^k\) avec bonne capacité de détection

Codage d’un message dans \(GF(q)^l\):

  1. Découpage du message en \(k\) blocs, chaque bloc étant interprété comme un polynôme de degré \(<d\) dans \(GF(q)[X]\) :

    \[P_1, \ldots, P_k\]

  2. Premier étage: évaluation et entrelacement.

    On construit la séquence suivant avec \(l\) blocs de longueur \(k\):

    \[\underbrace{P_1(x_1),P_2(x_1),\ldots,P_k(x_1)}, \underbrace{P_1(x_2),P_2(x_2),\ldots,P_k(x_2)},\ldots \underbrace{P_1(x_l),P_2(x_l),\ldots,P_k(x_l)}\]

  3. Codage de chacun des \(l\) blocs de longueur \(k\) avec P

Décodage:

  1. On utilise D pour détecter les blocs corrompus. On les jette.

  2. S’il en reste au moins \(d\): on déterminer chaque \(P_i\) à partir de ses valeurs sur \(d\) points d’évaluation.