Coding theory#
\(\newcommand{\ZZ}{\mathbb{Z}}\newcommand{\NN}{\mathbb{N}}\)
Some References:
«Agrégation» texts:
Introduction#
Purpose of coding theory#
A sender Alice transmits a message \(m\) to Bob over a noisy channel.
Issue:
How can Bob detect the existence of transmission errors?
How can Bob correct any errors
Note:
Unlike cryptography, the issue is not to protect from a malicious third party, but against random noise.
Examples of applications#
NASA/CNES/…: communication with probes and satellites
CD / DVD
Data transfer over the Internet (TCP, CRC, MD5 checksum)
Mobile phones
What are the specific constraints of each of these applications?
First examples of codes#
Human languages!#
Syntax: spelling, grammar, vocabulary
English: \(500000\) words of average length \(10\), out of roughly \(26^{10}\); or a proportion of \(10^{-9}\).
Example: apple, apricot, poem (apple, pear, bonus, poem)
Semantics: meaning, context, …
Example: 7-bit parity coding#
Alice wants to send the message \(m = 0100101\)
It encodes it as an 8-bit word with an even number of 1s, adding a parity bit: \(c = 01001011\)
The code word \(c\) is transmitted and possibly corrupted.
Bob receives \(c'\) and looks for an even number of 1s.
If not, as for \(c' = 01101011\), \(B\) detects that there has been an error
If so, as for \(c' = 10001011\), \(B\) assumes that \(c=c'\)
First concepts#
Definitions
A code \(C\) is a subset of words in \(M:=A^{n}\), where
\(A\) is an alphabet, like \(A:=\ZZ/q\ZZ= \{0,1,...,q-1\}\) .
Typically \(q=2\) (binary codes).\(n\) is an integer, the dimension of the code
Coding: the message sent \(m\) is transformed into a word \(c\) of the code.
Transmission: passing through the channel, \(c\) becomes \(c'\).
Error detection: we try to determine whether \(c=c'\); approximation: we test whether \(c'\) is in \(C\)
Error correction: we try to recover \(c\) from \(c'\).
Decoding: the message \(m\) is found from \(c\).
Hamming distance decoding#
Definition
Hamming distance between two words: number of letters that differ (comparing letter to letter).
Strategy:
Error detection: is \(c'\) in the code \(C\)?
Minimum distance error correction: we return the word \(C\) closest to \(c'\).
Exercise: Is this reasonable?
It is assumed that, during transmission, each letter has a probability \(p\) of being corrupted, independently of the others.
Calculate the probability that a word of length \(n\) will arrive intact? With one error at most? With no more than two errors?
Numerical application:
n = 7; p = 0.1
(1-p)^n
(1-p)^n + n*p*(1-p)^(n-1)
(1-p)^n + n*p*(1-p)^(n-1) + binomial(n,2) * p^2*(1-p)^(n-2)
n = 7; p = 0.01
(1-p)^(n-1)
(1-p)^n + n*p*(1-p)^(n-1)
(1-p)^n + n*p*(1-p)^(n-1) + binomial(n,2) * p^2*(1-p)^(n-2)
Definitions
Detection capacity: \(D(C)\) maximum number of errors that are guaranteed to be detected
Correction capacity: \(e(C)\) maximum number of errors that are guaranteed to be corrected
Distance \(d(C)\) of the code: minimum distance between two distinct points from the code
Formalisation#
To formalise this, it is convenient to introduce the notion of a ball naturally associated with a metric: given \(x\in M\) and an integer \(k\geq 0\), the ball of centre \(x\) and radius \(k\) is:
So:
Degenerate cases#
When \(|C|\leq 1\), we will take by convention \(d(C)=+\infty\). This may seem more natural if you take the alternative definition:
Exercise: in small dimensions
We fix \(A=\ZZ/2\ZZ\) (binary codes).
Find all the codes of \(M=A^n\) for \(n=1\), \(n=2\), \(n=0\).
For each of them, give the distance \(d(C)\), the detection capacity \(D(C)\), the correction capacity \(e(C)\). Draw the spheres with centres in \(C\) and with the radius \(e(C)\).
Do they allow us to correct a mistake?
Give a code from \(M=A^3\) for correcting an error.
Can we do better?
Proposition
Detection capacity: \(D(C) = d(C) - 1\).
Correction capacity: \(e(C) = \llcorner\frac{d(C)-1}2\lrcorner\).
Hamming terminal, perfect codes#
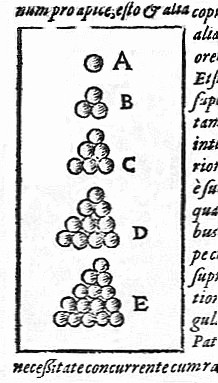
Problem: Discrete Kepler
An alphabet is set \(A\) with \(q=|A|\), a dimension \(n\) and a correction capacity \(e\). How many words can be coded at most?
Equivalently: how many non-intersecting spheres of radius \(e\) can we fit into \(M\)?
Examples: visualisation of spheres of radius \(e\) around some binary codes
Loading of quelques fonctions, and configuration of the 3D plots:
%run "codes_correcteurs.py"
from sage.plot.plot3d.base import SHOW_DEFAULTS
SHOW_DEFAULTS['frame'] = False
SHOW_DEFAULTS['aspect_ratio'] = [1,1,1]
SHOW_DEFAULTS['viewer'] = 'threejs'
The spheres in \(M=A^3\) for \(A=\mathbb{Z}/q\mathbb{Z}\):
@interact
def _(r=slider(0,3,1), q=slider(2,7,1)):
A = IntegerModRing(q)
M = A^3
return dessin_boules([M([1,1,1])], r)
The threefold repetition binary code:
A = GF(2)
M = A^3
C = M.subspace([[1,1,1]])
C.list()
dessin_boules(C,1)
and on \(A=\mathbb{Z}/3\mathbb{Z}\):
A = GF(3)
M = A^3
M.list()[:9]
C = M.subspace([[1,1,1]])
C.list()
dessin_boules(C,1)
The Hamming code:
A = GF(2)
M = A^7
C = codes.HammingCode(A, 3)
C.cardinality()
dessin_boules(C, 1, projection=projection_7_3)
Exercise: Hamming limit on \(|C|\).
Let \(A=\mathbb{Z}/q\mathbb{Z}\).
Figure out the cardinality of the ball \(B(x,e):=\{y,\quad d(x,y)\leq e\}\) of \(A^n\) of centre \(x\) and radius \(e\)? Hint: start with \(q=2\) and \(x=0\cdots0\).
Cardinality of \(A^n\)?
Conclusion?
Solution
+$\(|B(x,e(C))| = \sum_{k=0}^{e(C)} \binom n k (q-1)^k \qquad \qquad |C||B(x,e)| \quad \leq \quad q^n\)$
Numerical application:
@interact
def _(q=slider(1,7,default=2), n=slider(0,10, default=3), e=slider(0,10,default=1)):
m = q^n
b = sum(binomial(n,k)*(q-1)^k for k in range(0, e+1))
print(f"|M|={m}, |B(x,e(C))|={b}, |C|≤ {1.0*m/b:.2}")
Definition: perfect code
A code \(C\) is perfect if we have equality: \(|C| |B(x,e(C))| = |A^n|\)i.e.
Examples
In all the examples seen so far, the only perfect codes are the trivial codes, the triple repetition code on a two-letter alphabet and the Hamming code.
Problem
Encoding? decoding algorithms?
Linear codes#
Principle: we add structure to make the algorithms more efficient.
Definition
A linear code is a vector subspace of \(A^n\), where \(A\) is a finite field.
Let’s start with a little warm-up.
Exercise: linear algebra on \(A=\mathbb{Z}/2\mathbb{Z}\), by hand
Let \(H\) be the matrix:
A = GF(2); A
H = matrix(A, [[0,1,1,1, 1,0,0],
[1,0,1,1, 0,1,0],
[1,1,0,1, 0,0,1]]); H
Apply the gaussian pivot to \(H\).
Are the vectors \((1,1,0,0,1,1,0)\) and \((1,0,1,1,1,0,1)\) in the vector subspace generated by the lines of \(H\)?
Conclusion?
Solution:
H[1], H[0] = H[0], H[1]
H
H[2] = H[2] + H[0]
H
H[2] = H[2] + H[1]
H
H[0] = H[0] + H[2]
H[1] = H[1] + H[2]
H
u = vector(A, (1,1,0,0,1,1,0))
v = vector(A, (1,0,1,1,1,0,1))
Question: is \(u\) in the vector subspace generated by the lines of \(H\)?
We are looking for \(a,b,c\) such that \(u = a H[0] + b H[1] + c H[2]\)
u
u = u - H[0]
u
u = u - H[1]
u
Thereby, \(u\) is in the subspace spanned by the rows of \(H\).
v
v = v - H[0]
v
v = v - H[2]
v
Thereby, \(v\) is not in the subspace spanned by the rows of \(H\).
So \(v\) is not in the subspace
Examples#
Example: parity bit
Seven bits plus an eighth bit called parity such that the total number of bits at \(1\) is even.
v: my word
\(v_0 + v_1 + v_2 + v_3 + v_4 + ... + v_7=0\) if the number of bits at is even
Example: Hamming code \(H(7,4)\).
Four bits \(\left(a_{1},a_{2},a_{3},a_{4}\right)\) plus three redundancy bits \(\left(a_{5},a_{6},a_{7}\right)\) defined by:
Algorithms#
How to test if a word belongs to the code?#
With Sage:
A = GF(2); A
n = 7
M = A^7; M
Control matrix:
H = matrix(A, [[0,1,1,1, 1,0,0],
[1,0,1,1, 0,1,0],
[1,1,0,1, 0,0,1]])
Code belonging test:
mot_du_code = M([1,0,1,1,0,1,0]);
H * mot_du_code
mot_quelconque = M([1,1,0,1,0,1,1]);
H * mot_quelconque
Do it again by hand!
The code itself is the kernel of \(H\):
C = H.right_kernel()
C
mot_du_code in C
mot_quelconque in C
Do it again by hand!
Could \(C\) be found even faster?
Yes:
MatrixSpace(A,4,4)(1).augment(H[:,0:4].transpose())
Exercise:#
How many words are there in the Hamming code \(C=H(7,4)\)?
Calculate the distance of this code (hint: go to zero!)
What is its detection capacity? Is it perfect?
Solution:
C.cardinality()
def poids(c): return len([i for i in c if i])
poids(M([0,1,0,0,0,0,0]))
poids(M([1,0,1,1,0,1,0]))
min(poids(m) for m in C if m)
How can we code a message into a code word?#
Generating matrix:
G = C.matrix(); G
M = A^4
m = M([1,0,1,0])
c = m * G; c
How can we decode a code word in a message?#
Due to the shape of the generating matrix:
G
the code word c is simply obtained by adding extra bits
to the end of the original word. This is a desirable property of
corrective codes as it allows for a clear separation of
original and redundant information. In particular,
decoding is trivial: we only need to recover the first four bits.
Examples: the control key for your social security number.
Error correction by syndrome#
Exercise
Start with the word zero, code it, and alternately make an error on each of the bits. Record the result after multiplication by the control matrix.
Take a 4-bit word of your choice, code it, make an error on one of the 7 bits, correct and decode. Check the result.
What happens if there are two errors?
Let \(c\) in the code: then \(H c = 0\)
After transmission, the result is \(c' = c + 𝜖\), where \(𝜖\) is the error.
So: \(H c' = H (c + 𝜖) = H c + H 𝜖 = H 𝜖\)
We see \(𝜖\) as a disease and \(𝜖\) as a syndrome of the disease: what we have just calculated is that two patients with the same disease will have the same syndrome. The reverse is true as long as \(𝜖\) remains within the capacity of correction (prove it!).
This gives us the following syndrome decoding scheme:
Pre-calculate all syndromes \(H𝜖\) for all « diseases » \(𝜖\) in the correction capacity, and make it into a table.
To correct \(c'\), we calculate its syndrome \(Hc'\). If it is zero, \(c'\) is already in the code: \(c=c'\). Otherwise, we find the table contains \(𝜖\) such as \(Hc'=H𝜖\), and correct \(c'\) by \(c=c'-𝜖\).
Cyclic codes#
Principle: even more structure to be even more efficient.
Definition
A code \(C\) is cyclic if it is stable by word rotation:
Practitioners have noted that cyclic codes had good properties.
Let’s give a structure of quotient ring to \(M=A^n\) by identifying it with \(A[X]/(X^n-1)\).
Under this identification, the words above correspond to
Note
In \(A[X]/(X^n-1)\), shift = multiplication by \(X\).
For example, for \(A[X]/(X^7-1)\):
Ideal \(\longleftrightarrow\) cyclic codes in \(A[X]/(X^n-1)\).
Let \(g\) be a divisor of \(X^n-1\), and \(h\) such that \(gh=X^n-1\).
Code: ideal generated by \(g\)
Coding: \(m\mapsto c = mg\)
Error detection: \(c*h=0\)
Decoding: division by \(g\) modulo \(X^n-1\) (e.g. by Euclid extended)
BCH codes
Cyclic codes with a predetermined correction capacity can be constructed and determined in advance. For more information, see Wikipedia, BCH Code.
Interpolation coding (Reed-Solomon)#
Exercise (shared secret)
An old pirate is on his deathbed. In his youth he buried a Fabulous Treasure in the lagoon of Turtle Island, somewhere east of the Grand Coconut Tree. He gathered his ten favourite lieutenants to give them the secret information: the distance between the Great Coconut Tree and the Treasury. Knowing his lieutenants well, and in an astonishing last gasp of justice, he would not want a conspiracy of a few of them to murder the others in order to pocket the treasure alone. However, taking into account the usual mortality of the group he wishes to give secret information to each of his lieutenants so that any eight of them can find the treasure together, but no less. How can he do it?
Application to coding: CIRC
Breakdown of information into blocks, interpreted as polynomials \(P_1,\dots,P_k\) in \(GF(q)[X]\).
Evaluation points \(x_1,\ldots,x_l\).
First stage: evaluation and interleaving.
Second stage: coding of each of the \(l\) blocks with a code used to detect errors.
