Adapting to the context: conditional instructions

Motivation: role of control structures

Hint

Reminder We have seen that the instructions of a program are executed sequentially

(one after the other), in the order in which they are given, as in the following

example.

Example

debut()
droite()
avance()
prend()
gauche()
avance()
pose()
droite()
avance()
gauche()
avance()
avance()
droite()
ouvre()

However, we often need to break this sequential execution:

• Either to adapt to the context:

  

• Or to repeat instructions:

  

For this, we need control structures. In this sheet, we

will explore how to adapt to the context with conditional statements.

Later, we will see how to repeat instructions.

Conditional Instructions

Introduction

The general principle is that, depending on a condition, we will

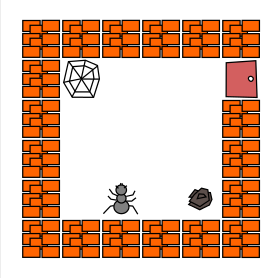
execute certain instructions or not. Let’s look at this on the first maze above

that you have already encountered:

from laby.global_fr import *
Laby(niveau="3a")

Run the following cell several times:

debut()
droite()
avance()
gauche()

You will have noticed that once the ant arrives at this point in the labyrinth, it faces, depending on the case,

either a large spider web (deadly!) or a small one. It must

therefore act differently depending on this context.

1. If it faces a large spider web, it must turn around to go through the other side of the labyrinth.

2. Otherwise, it faces a small spider web that it can cross safely.

Here’s how it can be written:

Laby(niveau="3a")

debut()
droite()
avance()
gauche()

if regarde() == Toile:
    gauche()
    avance()
    avance()
    droite()
    avance()
    avance()
    droite()
    avance()
    gauche()
else:
    avance()
    avance()
    gauche()
    avance()
    droite()

ouvre()

Conditional Statements

We will now formally introduce conditional statements, and first

specify how to group several instructions together as above (and

as previously previewed with functions; this is done in Python using

indentation:

Definition: Instruction Block

An bloc d’instructions (code block) is a sequence of one or more instructions to

execute successively. It is delimited by its indentation (by convention four

spaces more than the surrounding code) as well as by a ‘:’ on the preceding line:

    ...:

        instruction 1
        instruction 2
        ...
        instruction n

    ...

We can now define simple and alternative conditional statements.

Todo

ajouter un definiendum

Definition: Simple conditional statement: “if … then …”

Syntax:

if condition:
    bloc d instructions

Semantics

1. Evaluation of the condition

2. If its value is true, execution of the block of instructions

Example

if regarde() == Toile:     # Au secours, fuyons!
    gauche()
    gauche()

Definition: Alternative conditional instruction: “if … then … else …”

Syntax

if condition:
    bloc d instructions 1
else:
    bloc d instructions 2

Semantics

1. Evaluation of the condition

2. If its value is “True”, execution of instruction block 1

3. If its value is “False”, execution of instruction block 2

Example

if regarde() == Toile:    # Au secours, fuyons!
    gauche()
    gauche()
else:                     # Tout va bien
    avance()

Example: Calculating the maximum and minimum of two numbers

The four cells below illustrate the calculation of the maximum and minimum of two

numbers contained in variables x and y.

x = 3              # Les entrées
y = 5

if ( x > y ):
    maximum = x
    minimum = y
else:
    maximum = y
    minimum = x

minimum

3

maximum

5

Exercise

1. Test the following code with several values of \(a\) and \(b\). What does it do?

a = 10
b = 5

if a > b:
    print(a)
else:
    print(b)

10

Solution

It calculates the maximum between a and b and displays it.

Exercise

In this exercise, you will use the max function below to calculate the

maximum of two numbers, three numbers, and four numbers.

def max(a, b):
    if a > b:
        return a
    else:
        return b

n1 = -2
n2 = 6
n3 = 0
n4 = 7

Exercise (continued)

1. Calculate the max of n1 and n2 (using the max function):

### BEGIN SOLUTION
max(n1, n2)
### END SOLUTION

6

Exercise (continued)

2. Calculate the max of n1, n2 and n3 Hint: use the max function twice.

### BEGIN SOLUTION
max(n1, max(n2, n3))
### END SOLUTION

6

Exercise (continued)

3. Calculate the max of n1, n2, n3, and n4 (still using the max function):

### BEGIN SOLUTION
max(n1, max(n2, max(n3, n4)))
### END SOLUTION

7

Exercise (continued)

4. Change the values of n1, n2, n3, and n4 above, re-run the cells, and check the results.

Reminder: Exercises preceded by a ♣ are more difficult and optional. It is not

necessary to master them to move on.

Exercise (continued)

5. ♣ Write a function max4 that takes four integers and calculates their maximum:

### BEGIN SOLUTION
def max4(a, b, c, d):
    return max(a, max(b, max(c, d)))
### END SOLUTION

Exercise (continued)

6. ♣ Use your max4 function to calculate the maximum of n1, n2, n3 and n4:

### BEGIN SOLUTION
max4(n1, n2, n3, n4)
### END SOLUTION

7

Exercise

1. Complete the function min below. Hint see the example of the max function above and adapt it.

def min(a, b):
    ### BEGIN SOLUTION
    if ( a < b ):
        return a
    else:
        return b
    ### END SOLUTION

Exercise (continued)

2. Try it on the following example:

min(2,3)

2

Exercise (continued)

3. Try it on an example of your choice:

### BEGIN SOLUTION
min(6, 0)
### END SOLUTION

0

Exercise (continued)

4. Verify that all the following tests have the value true:

min(5, 10) == 5

True

min(6, -2) == -2

True

min(-3, -4) == -4

True

min(5, min(-3, 8)) == -3

True

Exercise (continued)

5. The following cell contains automated tests; we will come back to these in more detail later; execute the cell and verify that there are no error messages.

assert( min(5, 10) ==  5 )
assert( min(6, -2) == -2 )
assert( min(2,  2) ==  2 )

Exercise

1. Complete the function abs below that calculates the absolute value of a number:

def abs(a):
    ### BEGIN SOLUTION
    if ( a < 0 ):
        return -a
    else:
        return a
    ### END SOLUTION

Exercise (continued)

2. Use this function to calculate the absolute value of -2.5 and check the result:

### BEGIN SOLUTION
abs(-2.5)
### END SOLUTION

2.5

Exercise (continued)

3. Verify that the following tests have the value True:

abs(-5.1) == 5.1

True

abs(2.3) == 2.3

True

abs(-3.4) == 3.4

True

Exercise (continued)

4. Verify that the automated tests below do not produce an error:

assert abs( 0.0) == 0.0
assert abs( 2.3) == 2.3
assert abs(-3.4) == 3.4

We will now see how to handle contexts with more than two cases.

Definition: Chained conditional instruction: “if … then … else if … then else …”

Syntax

if condition1:
    bloc d instructions 1
elif condition2:
    bloc d instructions 2
else:
    bloc d instructions 3

Semantics

The code above is strictly equivalent to (but more readable than):

if condition1:
    bloc d instructions 1
else:
    if condition2:
        bloc d instructions 2
    else:
        bloc d instructions 3

There can be as many elif clauses as necessary.

Exercise

Complete the function frais_de_livraison below, which takes a distance in kilometers as a parameter

and returns the delivery costs based on this distance

according to the following rules:

• If the distance is less than or equal to 5 km, the delivery costs are €5.

• If the distance is between 5 km (exclusive) and 20 km (inclusive), the delivery costs are €10.

• If the distance is greater than 20 km, the delivery costs are €15.

def frais_de_livraison(distance):
    ### BEGIN SOLUTION
    if distance <= 5:
        return 5
    elif distance <= 20:
        return 10
    else:
        return 15
    ### END SOLUTION

assert frais_de_livraison(3) == 5
assert frais_de_livraison(10) == 10
assert frais_de_livraison(30) == 15

Conclusion

In this sheet, we have seen how to use simple

conditional instructions,

alternative or

nested instructions to adapt the behavior of the program according to the context, depending on the number of cases to be treated.

Before moving on, we offer some self-correcting training and review exercises.

import glob, os
from jupylates import Exerciser
os.chdir("../exercices")
Exerciser(glob.glob('conditions/*.md'))