Fonctions#
Prélude#
Exercices d’entraînement Jupylates#
J’ai travaillé des exercices d’entraînement Jupylates |
|
J’ai rencontré des problèmes techniques |
|
Je n’ai pas essayé |
|
Il y avait des exercices en ligne à notre disposition? |
Résumé des épisodes précédents …#
Pour le moment nous avons vu :
Expressions:
3 * (4+5),1 < x and x < 5 or y == 3
Variables, types, affectation:
int n = 1 + 1
Instructions conditionnelles:
if
Instructions itératives:
while,do ... while,for
Tout ce qui est calculable par un ordinateur peut être programmé
uniquement avec ces instructions
(ou presque : il faudrait un accès un peu plus souple à la mémoire)
Pourquoi aller plus loin?
Motivation: l’exemple du livre de cuisine (1)#
Recette de la tarte aux pommes
Ingrédients : 250 g de farine, 125 g de beurre, 1 œuf, 2 cl d’eau, une pincée de sel, 100 g de sucre en poudre, 5 belles pommes
Mettre la farine dans un récipient puis faire un puits
Versez dans le puits 2 cl d’eau
Mettre le beurre
Mettre le sucre et le sel
Pétrir de façon à former une boule
Étaler la pâte dans un moule
Peler les pommes, les couper en quartiers et les disposer sur la pâte
Faire cuire 30 minutes
Motivation : l’exemple du livre de cuisine (2)#
Recette de la tarte aux poires
Ingrédients : 250 g de farine, 125 g de beurre, 1 œuf, 2 cl d’eau, une pincée de sel, 100 g de sucre en poudre, 5 belles poires
Mettre la farine dans un récipient puis faire un puits
Versez dans le puits 2 cl d’eau
Mettre le beurre
Mettre le sucre et le sel
Pétrir de façon à former une boule
Étaler la pâte dans un moule
Peler les poires, les couper en quartiers et les disposer sur la pâte
Faire cuire 30 minutes
Motivation : l’exemple du livre de cuisine (3)#
Recette de la tarte tatin
Ingrédients : 250 g de farine, 125 g de beurre, 1 œuf, 2 cl d’eau, une pincée de sel, 200 g de sucre en poudre, 5 belles pommes
Mettre la farine dans un récipient puis faire un puits
Versez dans le puits 2 cl d’eau
Mettre le beurre
Mettre le sucre et le sel
Pétrir de façon à former une boule
Verser le sucre dans une casserole
Rajouter un peu d’eau pour l’humecter
Le faire caraméliser à feu vif, sans remuer
Verser au fond du plat à tarte
Peler les pommes, les couper en quartiers
Faire revenir les pommes dans une poêle avec du beurre
Disposer les pommes dans le plat et étaler la pâte au dessus
Faire cuire 45 minutes et retourner dans une assiette
Qu’est-ce qui ne va pas?#
Duplications
Longueurs
En cas d’erreur ou d’amélioration :
plusieurs endroits à ajuster!
Manque d’expressivité
Difficile à lire
Difficile à mémoriser
Recettes de base#
Recette de la pâte brisée
Ingrédients : 250 g de farine, 125 g de beurre, 1 œuf, 2 cl d’eau, une pincée de sel
Mettre la farine dans un récipient puis faire un puits
Versez dans le puits 2 cl d’eau
Mettre le beurre
Mettre le sucre et et une pincée de sel
Pétrir de façon à former une boule
Recette du caramel
Ingrédients : 100 g de sucre
Verser le sucre dans une casserole
Rajouter un peu d’eau pour l’humecter
Le faire caraméliser à feu vif, sans remuer
Recettes de tartes#
Tarte aux fruits (pommes, poires, prunes, …)
Ingrédients : 500g de fruits, ingrédients pour une pâte brisée
Préparer une pâte brisée
Étaler la pâte dans un moule
Peler les fruits, les couper en quartiers et les disposer sur la pâte
Faire cuire 30 minutes
Tarte tatin
Ingrédients : 5 belles pommes, ingrédients pour pâte brisée et caramel
Préparer une pâte brisée
Préparer un caramel et le verser au fond du plat à tarte
Peler les pommes, les couper en quartiers
Faire revenir les pommes dans une poêle avec du beurre
Disposer les pommes dans le plat, et étaler la pâte au dessus
Faire cuire 45 minutes et retourner dans une assiette
Les fonctions : objectif#
Modularité
Décomposer un programme en programmes plus simples
Implantation plus facile
Validation (tests)
Réutilisation
Flexibilité (remplacement d’un sous-programme par un autre)
Non répétition
Partager (factoriser) du code
Code plus court
Maintenance plus facile
Abstraction
Programmes plus concis et expressifs
Une impression de déjà vu? (1)#
while ( regarde() == Vide ) {
avance();
}
gauche();
while ( regarde() == Vide ) {
avance();
}
gauche();
while ( regarde() == Vide ) {
avance();
}
droite();
while ( regarde() == Vide ) {
avance();
}
droite();
while ( regarde() == Vide ) {
avance();
}
ouvre();
Une impression de déjà vu? (2)#
void avance_tant_que_tu_peux() {
while ( regarde() == Vide ) {
avance();
}
}
avance_tant_que_tu_peux();
gauche();
avance_tant_que_tu_peux();
gauche();
avance_tant_que_tu_peux();
droite();
avance_tant_que_tu_peux();
droite();
avance_tant_que_tu_peux();
ouvre();
Une impression de déjà vu? (3)#
Fonctions que vous avez déjà écrites :
TD1 :
transporte(Chèvre)TP1 :
avance_tant_que_tu_peux()TD2 :
max2(note1, note2),max3(note1, note2, note3), …TP3 :
factorielle(n), …
Fonctions#
Appels de fonctions usuelles#
Exemples#
Chargement de la bibliothèque de fonctions mathématiques usuelles :
#include <cmath>
Fonctions trigonométriques :
cos(3.141)
Fonction exponentielle :
exp(1.0)
Fonction puissance :
pow(3, 2)
pow(2, 3)
On remarque#
La présence de
#include <cmath>
C’est pour utiliser la bibliothèque de fonctions mathématiques
On y reviendra …
L’ordre des arguments est important
Le type des arguments est important
On sait ce que calcule
cos(x)!On ne sait pas comment il le fait
On n’a pas besoin de le savoir
Écrire ses propres fonctions : la fonction factorielle#
À la main#
Calculons \(5!\) :
int resultat = 1;
for ( int i = 1; i <= 5; i++ ) {
resultat = resultat * i;
}
resultat
Calculons 7! :
int resultat = 1;
for ( int i = 1; i <= 7; i++ ) {
resultat = resultat * i;
}
resultat
Avec une fonction#
int factorielle(int n) {
int resultat = 1;
for ( int i = 1; i <= n; i++ ) {
resultat = resultat * i;
}
return resultat;
}
factorielle(10)
factorielle(7)
factorielle(5) / factorielle(3) / factorielle(2)
Syntaxe d’une fonction#
Syntaxe
type nom(type1 parametre1, type2 parametre2, ...) {
déclarations de variables;
bloc d instructions;
return expression;
}
parametre1, parametre2, ...: les paramètres formels (formal parameter)Le type des paramètres formels est fixé
Les variables sont appelées variables locales (local variable)
À la fin, la fonction renvoie la valeur de
expression
Celle-ci doit être du type annoncé
Sémantique simplifiée de l’appel de fonction#
Revenons sur la fonction max
float max(float a, float b) {
if ( a >= b ) {
return a;
} else {
return b;
}
}
maxn’est utilisée que si elle est appelée
Pour appeler cette fonction on écrit par exemple
max(1.5, 3.0)
les paramètres
aetbsont initialisés avec les valeurs1.5et3.0
le code de la fonction est exécuté
l’exécution s’arrête au premier
returnrencontré
le
returnspécifie la valeur de retour de la fonction :
la valeur de l’expressionmax(1.5, 3.0)
Documentation et tests#
Documentation d’une fonction (syntaxe javadoc)#
Exemple
/** Fonction qui calcule la factorielle
* @param n un nombre entier positif
* @return n!
**/
int factorielle(int n) ...
Une bonne documentation :
Est concise et précise
Donne les préconditions sur les paramètres
Décrit le résultat (ce que fait la fonction)
Astuce pour être efficace
Toujours commencer par écrire la documentation
De toute façon il faut réfléchir à ce que la fonction va faire!
Tests d’une fonction#
Pas d’infrastructure standard en C++ pour écrire des tests
Dans ce cours, on utilisera doctest
Exemple :
int factorielle(int n) {
int resultat = 1;
for ( int i = 1; i <= n; i++ ) {
resultat = resultat * i;
}
return resultat;
}
CHECK( factorielle(0) == 1 );
CHECK( factorielle(1) == 1 );
CHECK( factorielle(2) == 2 );
CHECK( factorielle(3) == 6 );
CHECK( factorielle(4) == 24 );
Tests d’une fonction#
Astuces pour être efficace
Commencer par écrire les tests d’une fonction
De toute façon il faut réfléchir à ce qu’elle va faire!
Astuces pour être efficace (suite)
Tester les cas particuliers
Astuces pour être efficace (suite)
Tant que l’on est pas sûr que la fonction est correcte :
Faire des essais supplémentaires
Capitaliser ces essais sous forme de tests
Astuces pour être efficace (suite)
Si l’on trouve un bogue :
Ajouter un test caractérisant le bogue
Attention
Les effets de bord sont durs à tester!
Modèle d’exécution#
Motivation#
Exercice#
On considère la fonction incremente :
int incremente(int n) {
n = n + 1;
return n;
}
Quelles sont les valeurs de a et b après l’exécution des lignes
suivantes :
int a, b;
a = 1;
b = incremente(a);
Deux possibilités paraissent envisageables :
a=1etb=2a=2etb=2
Laquelle en C++?
Motivation
Comprendre précisément l”appel de fonction?
Exemple : appel de la fonction factorielle#
int factorielle(int n) {
int resultat = 1;
for ( int k = 1; k <= n; k++ ) {
resultat = resultat * k;
}
return resultat;
}
Que se passe-t-il lorsque l’on évalue l’expression suivante?
factorielle(1+2)
Appel de fonctions : formalisation#
Syntaxe
nom(expression1, expression2, ...)
Sémantique
Evaluation des expressions
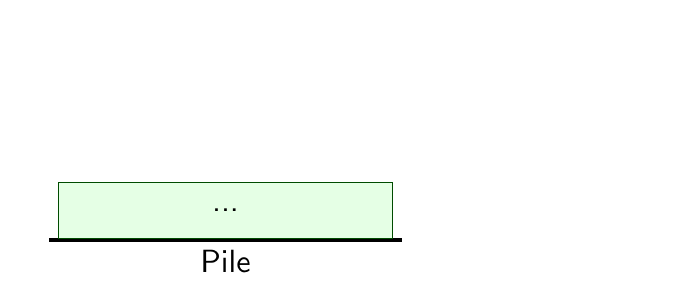
Leurs valeurs sont les paramètres réelsAllocation de mémoire sur la pile (stack) pour :
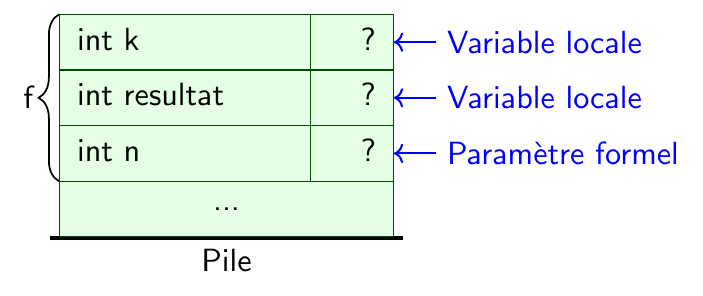
Les variables locales
Les paramètres formels
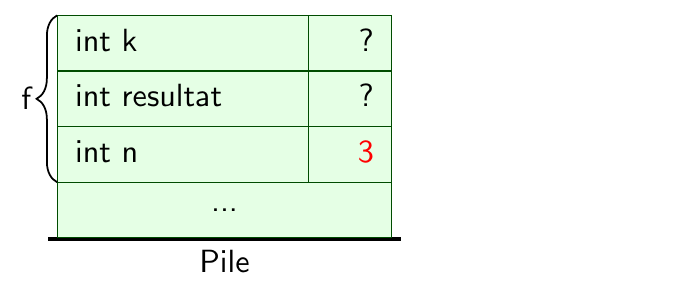
Affectation des paramètres réels aux paramètres formels
(par copie; les types doivent correspondre!)Exécution des instructions
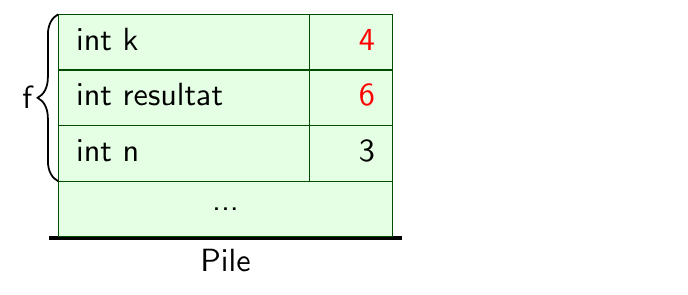
Lorsque
return expressionest rencontré, évaluation de l’expression qui donne la valeur de retour de la fonctionDésallocation des variables et paramètres sur la pile
La valeur de l’expression
nom(...)est donnée par la valeur de retour
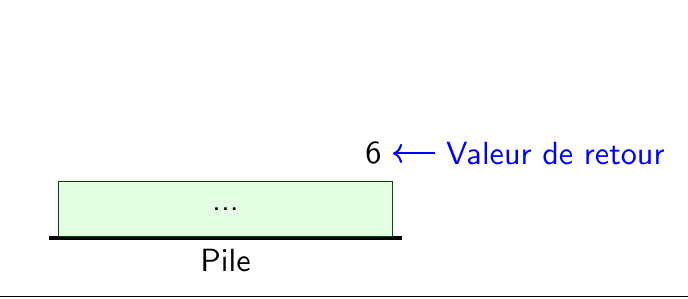
Évolution de la pile sur l’exemple#
État initial
Allocation de la mémoire sur la pile
3 : Affectation du paramètre réel au paramètre formel
4 : Exécution des instructions
5,6,7 : Désallocation de la mémoire sur la pile et valeur de retour
Appel de fonctions : retour sur l’exercice#
On considère la fonction incremente :
int incremente(int n) {
n = n + 1;
return n;
}
Appliquez la sémantique détaillée de l’appel de fonction pour
déterminer les valeurs de a et b après l’exécution des lignes
suivantes :
int a, b;
a = 1;
b = incremente(a);
Copier le code au tableau
Afficher la sémantique
Insister pour qu’ils fassent l’exercice avec papier et crayon
a
b
Passage des paramètres par valeur#
Les paramètres formels d’une fonction sont des variables comme les autres.
On peut les modifier.
Mais …
Rappel
Lors d’un appel de fonction ou de procédure, la valeur du paramètre réel est copiée dans le paramètre formel.
Conséquence
Une modification du paramètre formel n’affecte pas le paramètre réel
Si la variable est volumineuse (tableaux, chaîne de caractères, etc.), cette copie peut être coûteuse
On dit que les paramètres sont passés par valeur.
Au second semestre, vous verrez le passage de paramètres par référence.
Fonctions particulières#
Procédures
Fonctions récursives
Fonctions particulières : procédures#
Besoin de sous-programmes qui agissent au lieu de calculer :
On veut produire un effet (affichage, musique, etc)
On veut modifier l’état interne d’une structure de donnée
On parle d” effet de bord
Exemple
void avance_tant_que_tu_peux() {
while ( regarde() == Vide ) {
avance();
}
}
Cette fonction ne renvoie rien
On le dénote en C++ par le type
voidDans d’autres langages on distingue fonctions et procédures
Autres exemples :
transporte(...),gauche()
Fonctions particulières : fonctions récursives ♣#
Exemple
int factorielle(int n) {
if ( n == 0 ) {
return 1;
} else {
return n * factorielle(n-1);
}
}
Définition
Une fonction récursive est une fonction qui s’appelle elle-même.
Cela peut paraître étrange de définir un objet à partir de lui-même, mais c’est comme pour les suites définies par récurrence en mathématiques: il faut et il suffit de s’assurer d’avoir un cas de base et une étape de récurrence bien posée.
Exercice
Exécuter pas à pas :
factorielle(0)factorielle(3)factorielle(-1)
Résumé#
Motivation
Modularité
Lutte contre la duplication
Programmes plus concis et expressifs
Fonctions
Combinaison d’instructions élémentaires donnant une instruction de plus haut niveau
Modèle d’exécution (pile)
Procédures, fonctions récursives
Trilogie
Documentation : ce que fait la fonction (entrées, sorties, …)
Tests : ce que fait la fonction (exemples)
Code : comment elle le fait
Comment vous sentez-vous en ce début de cours?#
Curieux
Énervé
Inquiet
Fatigué