Ctrl+K

Cours: Initiation à la Science des données

Cours: Initiation à la Science des données#

Analyses de données#


Fanny Pouyet
L1 Informatique
Semestre 2

La semaine dernière

  • Définition et objectif de la science des données

  • Introduction à la bibliothèque Pandas et Numpy

Cette semaine

  • Présentation de plus de tests statistiques

  • Visualisation des données

  • Analyse de données

  • Modélisation avec un Modèles linéaires généralisés (GLM)

  • Bibliothèques Matplotlib et Seaborn

Contexte#

Dans ce cours, nous utiliserons l’exemple du jeu de données du Titanic, un énorme paquebot pour l’époque qui fait naufrage en 1912 à la suite d’une collision avec un iceberg, lors de son voyage inaugural de Southampton à New York.

  • Nous avons accès à des informations sur une partie des passagers (891 passagers) du Titanic.

  • Pourquoi certains passagers ont survécu et d’autres sont morts?

  • Commencons l’analyse de données

source :https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcSqRekfGrFFbNX1LxVcw5uy_kPRMBJfSvz9cA&usqp=CAU

Chargement des données#

Les données sont dans un tableau au format CSV (comma separated values):

import pandas as pd
import numpy as np
 
titanic = pd.read_csv("media/titanic.csv")

Ensuite, on OBSERVE ce qu’on a!!

titanic.head(10)

titanic.shape

titanic.describe(include='all')

Les colonnes sont:

  • PassengerId : Identifiant du passager

  • Survived : True (1) / False (0)

  • Pclass : Classe du ticket : 1, 2 ou 3.

  • Name : Nom du passager

  • Sex : Genre du passager (male/female)

  • Age : Age en années

  • Cabin : Numéro de cabine

  • Embarked : Port d’embarquement ( C : Cherbourg; Q Queenstown; S Southampton)

Question / objectif#

Pourquoi certains passagers ont survécu et d’autres sont morts?

On veut trouver les colonnes qui expliquent le 0/1 dans Survived et construire un modèle qui permettrait d’expliquer au mieux Survived étant donné nos informations.

  • On va commencer par observer nos données, en répondant à des questions descriptives:

  1. Quel sexe a le plus de chances de survie ?

  2. Est-ce que les enfants ont eu plus de chances de survie ?

  3. Quelle est la proportion de survie selon le port d’embarquement ?

Quel sexe a le plus de chances de survie ?#

  1. Comparaison de la proportion d’hommes et de femmes passagers du Titanic

  2. qui ont survécu

Utilisons groupby, qui permet de produire des tables de synthèses par catégories:

titanic.groupby(['Sex','Survived']).count()['PassengerId']

Autres tables de synthèse

passengers = titanic.groupby('Sex')['PassengerId'].count()
passengers

survivors = titanic.groupby('Sex')['Survived'].sum()
#pourquoi j'utilise sum() et pas count() ?
survivors

summary = pd.DataFrame({"Survivants": survivors,
                        "Passagers": passengers,
                        "%": round(100*survivors / passengers,1)})
summary

#Et au total ?
titanic['Survived'].sum() / titanic['PassengerId'].count()

Visualisation

import matplotlib.pyplot as plt
#Ici je représente un barplot car on a des catégories

Le même graphique, avec titre et labels:

summary[["Survivants", "Passagers"]].plot(kind='bar');
plt.xlabel('Sexe')
plt.ylabel('Total')
plt.title('Comparaison de la survie selon le sexe');

Conclusions

  • Observation :

    • 38% des passengers ont survécus et plus précisément 74% des femmes contre seulement 19% des hommes

    • Il y a plus d’hommes que de femmes sur le paquebot

  • Interprétation : Les femmes ont eu plus de chances de survivre que les hommes

Pour aller plus loin, on pourrait regarder à quel âge les hommes et femmes avaient la plus grande chance de survie.

Est-ce que les enfants ont eu plus de chances de survie ?#

  • On va commencer par séparer les enfants des adultes selon l’age. Problème, on a des données manquantes.

Gestion des données manquantes#

Il manque certaines informations. Que feriez-vous ?

On pourrait décider de supprimer les individus sans informations sur l’âge (pensez à vérifier les dimensions de votre table!)

print("Si j'enlève toutes les lignes contenant un 'NaN': ", titanic.dropna().shape)
print("\nSi je n'enlève que les 'NaN' de la colonne Age : ", titanic.loc[titanic['Age'].notna(),:].shape)

Maintenant on va créer une nouvelle colonne indiquant si l’on est adulte:

titanic['Adult'] = titanic['Age'] >=18  
titanic.head()

Et quid des individus dont on ne connait pas l’âge ?

titanic.head(n=6)

titanic_filt_age = titanic.loc[titanic['Age'].notna(),:]
passengers = titanic_filt_age.groupby(['Adult','Sex']).count()['PassengerId']
passengers

Il y a sur le bateau:

  • 55 enfants de sexe féminin

  • 58 enfants masculin

  • 206 adultes femmes

  • 395 adultes hommes

Quid des survivant.es ?

survivors = titanic_filt_age.groupby(['Adult','Sex'])['Survived'].sum()
survivors

Résumons et visualisons#

passengers = titanic_filt_age.groupby(['Adult','Sex'])['PassengerId'].count()
summary = pd.DataFrame({"Survivants": survivors,
                       "Passagers": passengers,
                       "%": round(survivors/passengers*100, 1)})
summary.index=['Girl','Boy','Woman','Man']
summary

#On représente ici un barplot car on a des catégories
summary.plot(kind='bar')
plt.xlabel("Personnes classées selon l'age et le sexe")
plt.ylabel('Total')
plt.title("Comparaison de la survie selon l'age et le sexe");

Conclusions

  • Observations:

    • Il y a plus d’adultes que d’enfants.

    • Ainsi, on a respectivement 69%, 40%, 77% et 18% de survivant-es parmi les filles, garcons, femmes et hommes.

  • Interprétation:

    Quelque soit la catégorie, les personnes de sexe féminin ont une plus grande chance de survie que les masculins. Les enfants de sexe masculin ont une plus grande chance de survie que les adultes mais ce n’est pas réciproque pour les personnes de sexe féminin. Pour aller plus loin, que pourrions nous regarder ?

Calculer la proportion de survie selon le port d’embarquement#

Observons les ports d’embarquement:

#Combien de ports y a t il ?
print(f'Nombre de ports:',titanic['Embarked'].nunique())
#Liste des noms de ports
print(f'Liste des ports:',titanic.loc[:,'Embarked'].unique())
titanic.groupby(['Embarked']).count()

La colonne du port d’embarquement à des valeurs manquantes (889 disponibles/891). Comme la plupart des passagers et passagères sont montées à Southampton, on peut supposer que les données manquantes viennent de là.

Attention ceci est un choix. Toujours garder en tête qu’il modifie vos résultats et peut donc modifier vos interpétations ! Ici, c’est vraiment à la marge

titanic["Embarked"] = titanic["Embarked"].fillna('S')

survivors_per_port = titanic.groupby('Embarked')['Survived'].sum()
passengers_per_port = titanic.groupby('Embarked')['PassengerId'].count()
comparaison_port_survie = pd.DataFrame({"Survivants": survivors_per_port,
                                        "Passagers": passengers_per_port,
                                        "%": round(survivors_per_port/passengers_per_port*100, 1)})
comparaison_port_survie

comparaison_port_survie.plot(kind='bar')
plt.xlabel("Port d'Embarquement")
plt.ylabel("Nombre d'individus")
plt.title('Comparaison de survie selon le port')

La figure indique que:

  • la plupart des individus sont montés à Southampton puis Cherbourg puis Queenstown.

  • le nombre de survivants et survivantes est plus grand selon le meme ordre.

  • Respectivement 219/646; 93/168 et 30/77 ont survécus selon le port d’embarquement Southampton, Cherbourg, Queenstown.

  • L’analyse de proportionnalité nous informe que les individus étant montés à Cherbourg ont eu plus de chance de survie. Pourquoi cela ?

C’est quoi la corrélation ? Et la causalité ?#

Il existe trois types de relations statistiques:

  • corrélation positive: si une variable augmente, l’autre aussi.

  • corrélation négative: si une variable augmente, l’autre diminue.

  • absence de corrélation: si une variable augmente, l’autre peut ou pas varier sans lien entre elle.

Exemple de corrélation:

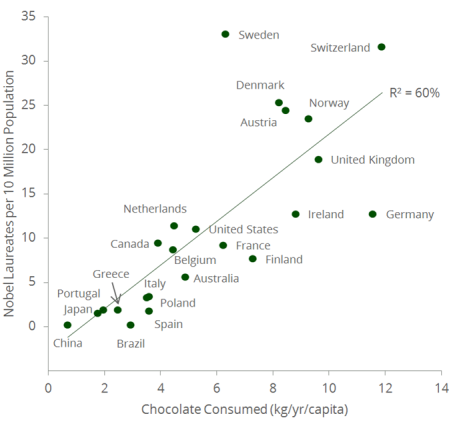
Chocolat et Prix Nobels

Cette corrélation est tirée d’un papier de 2012 par F. Messerli.

C. Pissarides, prix Nobel d’économie en 2010 suite à ce papier à commenté:

« To win a Nobel Prize you have to produce something that others haven’t thought about - chocolate that makes you feel good might contribute a little bit. Of course it’s not the main factor but… anything that contributes to a better life and a better outlook in your life then contributes to the quality of your work. »

  1. Décrivez la figure

  2. Qu’est-ce qu’on observe?

  3. Qu’en conclut-on?

Depuis, il a été montré que la corrélation positive est due à la richesse économique (economic wealth).

Alors qu’est ce que la causalité ?

Dans notre exemple, la richesse économique implique

  • une plus grande dépense en recherche

  • ce qui implique une corrélation positive avec le nombre de prix Nobel.

Par ailleurs et indépendamment, la richesse économique implique :

  • de plus grandes dépenses dans les produits de luxe, dont le chocolat.

Causalité n’est pas corrélation#

  1. Les corrélations relèvent de l”observation;

  2. Les causalités relèvent de l”interprétation !

♣ Pour vous montrer par l’exemple que correlation ne veut pas dire causalité, faites un tour ici:

https://www.tylervigen.com/spurious-correlations

https://www.lemonde.fr/les-decodeurs/article/2019/01/02/correlation-ou-causalite-brillez-en-societe-avec-notre-generateur-aleatoire-de-comparaisons-absurdes_5404286_4355770.html

Pour comprendre les biais d’interprétation induits par les représentations graphiques faites un tour là:

https://www.lemonde.fr/les-decodeurs/article/2018/05/22/sept-conseils-pour-ne-pas-se-faire-avoir-par-les-representations-graphiques_5302680_4355770.html

Retour au port d’embarquement. Pourquoi on survit plus si on a embarqué a Cherbourg ?

Hypothèse 1: Il y a plus de femmes à Cherbourg (?)

Hypothèse 2: On est plus riche à Cherbourg et plus on est riche plus on a survécu (?)

Hypothèse 1: Il y a plus de femmes à Cherbourg

female_per_port = titanic[titanic['Sex']=='female'].groupby('Embarked')['PassengerId'].count()
male_per_port = titanic[titanic['Sex']=='male'].groupby('Embarked')['PassengerId'].count()
pd.DataFrame({"Female": female_per_port,
              "Male" : male_per_port,
              "Total": passengers_per_port,
              "% Female": female_per_port / passengers_per_port
              })

Il n’y a pas plus d’individus féminins à Cherbourg qu’à Queenstown.

Hypothèse 2: on est plus riche à Cherbourg et plus on est riche plus on a survécu (?)

survivors_per_class = titanic.groupby('Pclass')['Survived'].sum()
passengers_per_class = titanic['Pclass'].value_counts()
pd.DataFrame({"Survivants": survivors_per_class,
              "Passagers": passengers_per_class,
              "%": round(survivors_per_class/passengers_per_class*100, 1)})

Il y a une nette corrélation entre la classe et la probabilité de survie!

On peut même l’expliquer causalement !

Regardons la répartition entre classes, selon le port d’embarquement

pclass1_per_port = titanic[titanic['Pclass']==1].groupby('Embarked')['PassengerId'].count()
pclass2_per_port = titanic[titanic['Pclass']==2].groupby('Embarked')['PassengerId'].count()
pclass3_per_port = titanic[titanic['Pclass']==3].groupby('Embarked')['PassengerId'].count()


pd.DataFrame({'Classe 1': pclass1_per_port,
              'Classe 2': pclass2_per_port,
              'Classe 3': pclass3_per_port,
              'Passengers': passengers_per_port,
              '% Classe 1': round(pclass1_per_port/passengers_per_port*100,1)})

Observations

  • Les passagers ayant embarqué à Cherbourg regroupent principalement des individus de première classe.

  • Les 77 passagers qui embarquent à Queenstown (Irlande) sont principalement de la classe 3 des migrants en route vers les États-Unis.

Conclusions

  • Les passagers ayant embarqué à Cherbourg arrivent de Paris (France) et sont plutôt riches.

  • Les 77 passagers qui embarquent à Queenstown (Irlande) sont principalement des migrants en route vers les États-Unis.

  • Il semble que la classe plus que le port d’embarquement a une relation de causalité avec la survie (à vérifier).

Corrélation (point mathématique)#

Le coefficient de corrélation linéaire de Pearson se calcule facilement en python . Il correspond à la version normalisée de l’écart-type par la standard deviation (écart-type) de la covariance.

Mathématiquement, on a: \(\rho_{xy} = \frac{\sigma_{xy}}{\sigma_x\sigma_y}\)

\(\rho_{xy}\) varie entre -1 et 1 et représente la force de la relation linéaire qui existe entre les 2 vecteurs/séries.

  • 0 : pas de corrélation

  • 1 : corrélation positive parfaite (si on connait \(x\) alors on peut déduire \(y\), les points sont alignés le long d’une droite)

  • -1: corrélation négative parfaite (idem)

  • en réalité, on a souvent des corrélations intermédiaires

« The intention of this contribution was to show that the correlation between chocolate consumption per capita and the number of Nobel laureates per capita (as reported by Messerli, 2012) will vanish if one controls for relevant other variables and if one uses a sophisticated estimation technique. » par Prinz A. L. (2020)

Chocolat et autres

On peut calculer la matrice de corrélation qui correspond à la corrélation entre les colonnes d’une table, et utiliser une carte de chaleur (heatmap en anglais) pour mieux la visualiser:

titanic_cor = titanic.corr(numeric_only=True)
titanic_cor.style.background_gradient(cmap='coolwarm', axis=None)
#remarque on ne peut pas calculer de correlation linéaire 
#avec des données ayant plus de 2 catégories comme le port d'embarquement
# il faudrait faire une ANOVA (hors programme)

Attention: par défaut, pour attribuer des couleurs aux nombres dans une carte de chaleur, Pandas applique une standardisation par colonne. Le axis=None assure que la normalisation est appliquée à l’ensemble des valeurs de la table.

Variante, avec la bibliothèque Seaborn:

import seaborn as sns

sns.heatmap(titanic_cor, fmt='0.2f', annot=True, square=True);

Représentation des données à l’aide de pair plots.

  • On a un aperçu rapide en une seule ligne de code

  • En diagonale, la distribution des valeurs de la colonne selon un histogramme

  • Pour le reste, des scatter plots (un point = une case)

  • Mais c’est lourd et lent. Ça ne marche pas avec un gros jeu de données

  • Tout n’est pas intéressant…

sns.pairplot(titanic, hue="Survived", diag_kind="hist", vars=['Sex','Age','Embarked','Pclass'])

Et maintenant ?#

On peut proposer un modèle d’explication de nos données.

Modèles d’arbres de décision#

Lorsque les variables ne sont pas continues la regression linéaire n’est pas possible. Rappelez vous les problèmes de visualisation avec nos pair plots.

Un modèle d’arbre de décision est un outil simple et visuel utilisé pour classer des données en fonction de plusieurs caractéristiques. À chaque étape (nœud), le modèle pose une question sur une caractéristique (ex. : « Le passager est-il un homme ? ») pour diviser les données en groupes plus homogènes. Ce processus se répète jusqu’à ce qu’une décision soit prise (feuille). Dans notre cas, l’objectif est de prédire si un passager du Titanic a survécu ou non, en utilisant des informations comme son âge, son sexe, sa classe, etc. Ce modèle est intuitif et utile pour comprendre comment les décisions sont prises à partir des données.

Dans ce cours, nous utiliserons une petite dizaine de modèles de classificateur. Nous ne ferons que les utiliser un peu comme des boîtes noires (pas de maths)

Étapes d’utilisation d’un classificateur#

  1. Construction du modèle :

    1. Un modèle

    2. Des attributs (cibles et variables)

    3. Des données (apprentissage, test)

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Definition de la cible et des variables
target = 'Survived'
features = ['Pclass', 'Sex', 'Age', 'Embarked']

# Preprocess les données
X = titanic_filt_age[features].copy()
y = titanic_filt_age[target]

# Gestion des données manquantes
X.loc[:, 'Age'] = X['Age'].fillna(X['Age'].median())
X.loc[:, 'Embarked'] = X['Embarked'].fillna(X['Embarked'].mode()[0])

# Encodage des données catégoricielles
X = pd.get_dummies(X, drop_first=True)

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,random_state=134)

  1. Ajustement du modèle aux données avec .fit()

tree_model = DecisionTreeClassifier(max_depth=3,random_state=134)
tree_model.fit(X_train, y_train)

  1. Description du modèle

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

# Plot the decision tree
plt.figure(figsize=(12, 8))  # Adjust figure size for better readability
plot_tree(tree_model, 
          feature_names=X.columns,  # Feature names for readability
          class_names=['Died', 'Survived'],  # Target class names
          filled=True,  # Color the nodes based on the class
          rounded=True,  # Rounded corners for better appearance
          fontsize=10,
          label="none", # Only shows splitting criteria
          impurity=False,  # Suppress Gini index
          proportion=False)# Font size for labels
plt.show()

  1. Précision du modèle

# Predictions
y_pred = tree_model.predict(X_test)

print("Accuracy:", accuracy_score(y_test, y_pred))

Qu’est-ce que la précision ?#

L’accuracy, ou taux de précision, mesure à quel point un modèle fait des prédictions correctes. C’est le pourcentage de bonnes réponses parmi toutes les prédictions.

\(Accuracy = \frac{Nombre de prédictions correctes}{Nombre total de prédictions}\)

Limites : Si les classes sont déséquilibrées (par exemple, beaucoup de passagers n’ont pas survécu), un modèle peut avoir une bonne précision sans bien faire son travail.

Conclusions#

  • Initiation à la science des données

    • l’observation est primordiale, l’interprétation vient après

    • les modèles linéaires ne sont parfois pas suffisant

  • Langage Python 3

    • Pandas, pour la structuration et la manipulation de tables

    • Numpy, pour les calculs scientifiques

    • MatplotLib, pour la visualisation de base (lib la plus utilisée)

    • Seaborn, pour la visualisation de graphiques statistiques. S’utilise entre autres avec des objets Pandas.

    • (Statsmodels, pour faire un modèle)

Perspectives#

  • TP 2

    • Utilisation de Pandas, Numpy, Matplotlib et Seaborn

    • Un autre jeu de données

    • Travail en binome

    • TP noté

  • CM 3 : analyse de données et classification d’images

    • Chaine d’analyse des données entière: VI-ME-RE-BAR

    • Interprétation des résultats

Contenu