Cours 5: Classificateurs en apprentissage statistique#
Précédemment
Chaine de traitement d’analyse de données
Application aux images : extraction de features
Cette semaine
Introduction aux différentes catégories de classificateurs en apprentissage statistique
Qu’est-ce que l’apprentissage statistique (machine learning) ?#
« L’apprentissage est une modification d’un comportement sur la base d’une expérience », Fabien Benureau (thèse, 2015).
La sortie d’un programme classique utilise les données d’entrée et une procédure explicitement programmée. L’apprentissage statistique estime les valeurs des paramètres de la procédure afin de modéliser un phénomène (la sortie) à partir d’exemples (l’entrée).
Objectifs de l’apprentissage statistique#
L’apprentissage statistique permet de résoudre des problèmes
qu’on ne sait pas résoudre par une procédure explicite ;
qu’on ne sait pas formaliser algorithmiquement (exemple: la classification d’images) ;
qu’on saurait résoudre, mais seulement avec des programmes trop gros informatiquement (mémoire, temps).
L’interprétation des modèles d’apprentissage statistique peut nous permettre d’identifier les attributs importants (ou pas).
Besoins de l’apprentissage statistique#
L’apprentissage statistique a besoin, de façon équivalente, de :
bonnes données et en quantités relativement importantes ;
d’un algorithme d’apprentissage:
une procédure
des paramètres
de l’optimisation (partie très mathématique, hors du cadre du cours)
Aujourd’hui je vais vous présenter différents algorithmes (la partie procédure).
Est-ce de l’intelligence artificielle ?#
Selon l’encyclopédie Larousse, l’IA est «l’ensemble des théories et des techniques mises en œuvre en vue de réaliser des machines capables de simuler l’intelligence humaine»
Toutefois, les machines se contentent toujours au final d’executer un programme, dont les valeurs des paramètres ne sont pas explicitement fixés. C’est ce comportement que l’on peut qualifier d’intelligent.
L’apprentissage statistique est une branche de l’intelligence artificielle (IA). Dans ce cours, on confond les deux et on garde à l’esprit qu’au fond ce sont des mathématiques.

Problèmes d’apprentissage statistique#
Il existe trois grandes classes:
Apprentissage supervisé : prédictions à partir d’une partie du jeu de données sans étiquettes (comme la classification d’images, ce qu’on fait dans ce cours).
Apprentissage non supervisé (cf. ACP)
Apprentissage par renforcement : apprentissage au fur et à mesure, chaque instance fournit un bonus/malus au modèle (cf. apprentissage du jeu de go, échecs etc.)
C’est quoi l’apprentissage en informatique?#
Apprendre pour nous humains c’est savoir répéter, comprendre, interpréter, généraliser.
En informatique, l’apprentissage revient à minimiser le nombre d’erreurs d’une fonction. Les prédictions de la fonction ont pour paramètres les données d’entrée donc les attributs (et toutes les valeurs possibles) et pour sortie l’étiquette. On parle de fonction de coût (cost/loss function).
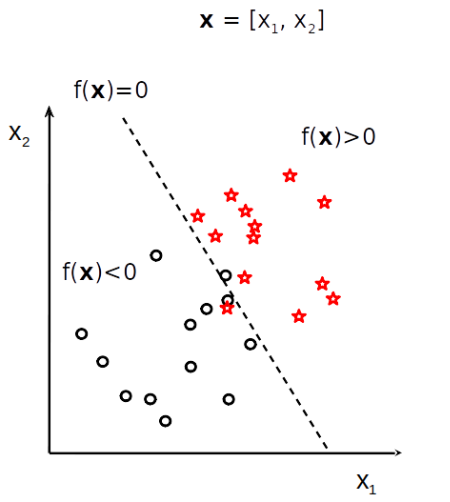
Les objectifs de l’apprentissage#
Le coût (loss) doit diminuer au fur et à mesure que le modèle apprend.
Et de facon similaire, la précision (accuracy) doit augmenter: c’est le nombre de prédicitons correctes.
Généralisation : capacité d’un modèle à faire des prédictions correctes sur de nouvelles données, qui n’ont pas été utilisées pour le construire.
Les limites des modèles
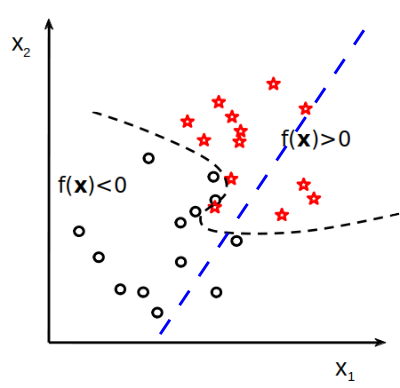
Sur-apprentissage ou overfitting (pointillés noirs):
Modèle qui capture les spécificités de notre ensemble d’entraînement (bruit, noise) mais, au fond, elles ne sont pas pertinentes pour notre problème.
fait de bonnes prédictions sur les données d’entraînement
mais généralise mal.
Sous-apprentissage ou underfitting (droite bleue):
mauvaises performances sur l’ensemble d’entraînement
et celui de test
On reparlera de ces concepts en fin d’UE (Semaine 8)
Apprentissage supervisé et classification#
Il existe deux catégories principales de méthodes pour un apprentissage supervisé d’un problème de classification:
Basée sur les exemples (example-based)
Comparaison de chaque échantillon à l’ensemble d’entraînement.
Avantages : simple; flexible.
Défauts : lent; beaucoup de mémoire.
Basée sur les attributs (features-based)
Création d’une règle qu’on applique ensuite aux échantillons à classifier.
Avantages : pas besoin de garder l’ensemble d’entraînement en mémoire.
Défauts : sensible aux filtrations.
Remarque : L’apprentissage statistique ne se résume pas à des problèmes de classification.
QUESTION: le KNN est-il example ou features-based ?
En Python, nous utilisons la librairie
scikit-learn
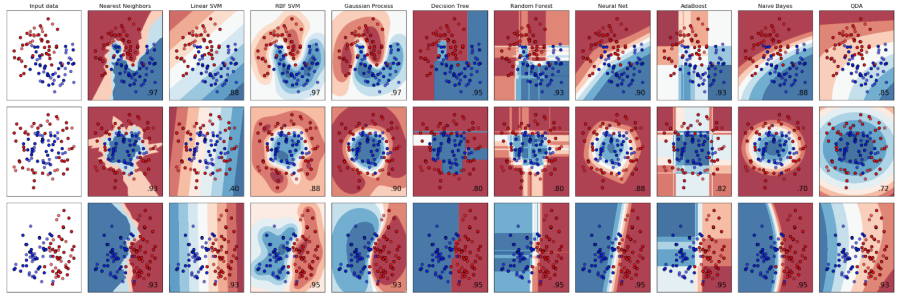
Exemples d’application#
Jeu de données iris
cinquante échantillons pour trois espèces d’Iris
Iris setosa, verginica, versicolor
quatre caractéristiques mesurées sur chaque échantillons:
longueur et largeur des sépales et des pétales

On souhaite classer les fleurs.
#Exemple avec le jeu de données de fleurs
from sklearn.datasets import load_iris
import numpy as np
import pandas as pd
# Hack: select which bytecode file to use for utilities_cours_correction depending on Python's version
import sys
ver = ''.join(str(i) for i in sys.version_info[:2])
!cp __pycache__/utilities_cours_correction.cpython-{ver}.pyc utilities_cours_correction.pyc
from utilities_cours_correction import *
iris = load_iris()
print(iris['target_names'])
X, Y = iris.data, iris.target
train_index, test_index = split_data(X, Y, verbose = True, seed=0)
Xtrain, Xtest = X[train_index], X[test_index]
Ytrain, Ytest = Y[train_index], Y[test_index]
Méthodes basées sur les exemples (example-based)#
Méthode des plus proches voisins KNN#
construction de frontières de décision complexe
modèle non-paramétrique : pas besoin d’hypothèses sur la distribution des données
les étiquettes du training set servent pour prendre une décision
Algorithmiquement:
définir la distance ou la similarité entre points n’est pas trivial (naturellement, on pense aux distances euclidiennes sur un graphe 2D)
from sklearn.neighbors import KNeighborsClassifier
#défintion du modèle et ajustement
knn_iris = KNeighborsClassifier(n_neighbors=5)
knn_iris.fit(Xtrain, Ytrain)
#prédictions
Ytrain_predicted = knn_iris.predict(Xtrain)
# le jeu de données de test permet de valider le modèle
Ytest_predicted = knn_iris.predict(Xtest)
# Calcul des erreurs
e_tr = error_rate(Ytrain, Ytrain_predicted)
e_te = error_rate(Ytest, Ytest_predicted)
print("CLASSIFICATEUR DU PLUS PROCHE VOISIN")
print("Training error:", e_tr)
print("Test error:", e_te)
Choix du \(k\) pour le KNN#
k=1 est très sensible au bruit
k=n (le nombre d’échantillons) est équivalent à un vote majoritaire
Quel est le bon k?
\(k\) intermédiaire
heuristiquement, \(k = \sqrt{n}\)
on peut faire varier \(k\) et comparer les différents modèles
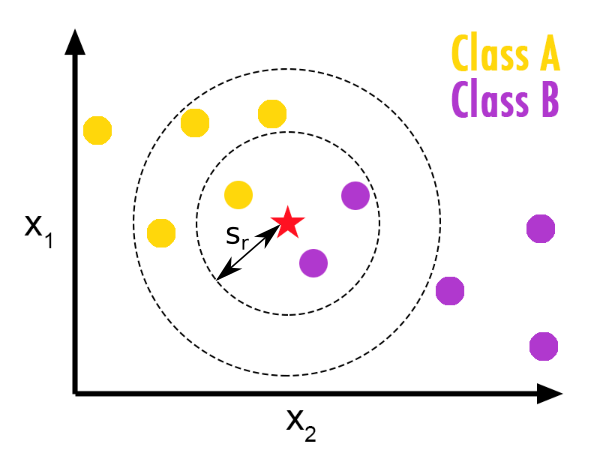
Fenêtres de Parzen (Parzen windows)#
L’élément à déterminer est classifié en fonction de la majorité des entités comprises dans une sphère centrée sur lui, de rayon \(r\).
Choix du \(r\) pour les fenêtres de Parzen (question en Projet 1)
from sklearn.neighbors import RadiusNeighborsClassifier
#défintion du modèle et ajustement
parzen_iris = RadiusNeighborsClassifier(radius=1)
parzen_iris.fit(Xtrain, Ytrain)
#prédictions
Ytrain_predicted = parzen_iris.predict(Xtrain)
Ytest_predicted = parzen_iris.predict(Xtest)
# Calcul des erreurs
e_tr = error_rate(Ytrain, Ytrain_predicted)
e_te = error_rate(Ytest, Ytest_predicted)
print("CLASSIFICATEUR DES FENETRES DE PARZEN")
print("Training error:", e_tr)
print("Test error:", e_te)
Méthodes basées sur les attributs (feature-based)#
Régression linéaire classique#
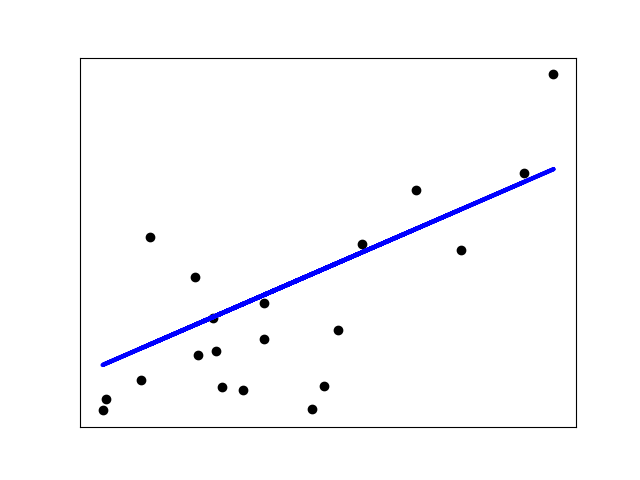
La séparation est une droite, une combinaison linéaire (= somme pondérée) des attributs.
Ne s’applique pas aux problèmes de classification car la régression linéaire sépare des données continues et non des classes discrètes.
L’étiquette n’est pas une classe mais la combinaison linéaire des attributs
from sklearn import linear_model
#données, en entrée besoin d'un 2Darray
xtrain = np.array([6, 8, 10, 14, 18]).reshape((-1, 1))
ytrain = np.array([7, 9, 13, 17, 18])
xtest = np.array([16]).reshape((1, -1))
ytest = 17
print("2D array x : ", xtrain,"\n")
#définition du modèle
model_linReg = linear_model.LinearRegression()
#entrainement du modèle
model_linReg.fit(xtrain, ytrain)
#prédiction entrainement
Ytrain_predicted = model_linReg.predict(xtrain)
print("y train: ", ytrain)
print("prediction de y train:" , Ytrain_predicted,"\n")
#prédiction test
Ytest_predicted = model_linReg.predict(xtest)
print( "y test :", ytest)
print("prediction de y test:" , Ytest_predicted)
Exercice bonus \(\clubsuit\)#
On peut quand même adapter cette technique à des problèmes de classification.
On crée une frontière de séparation
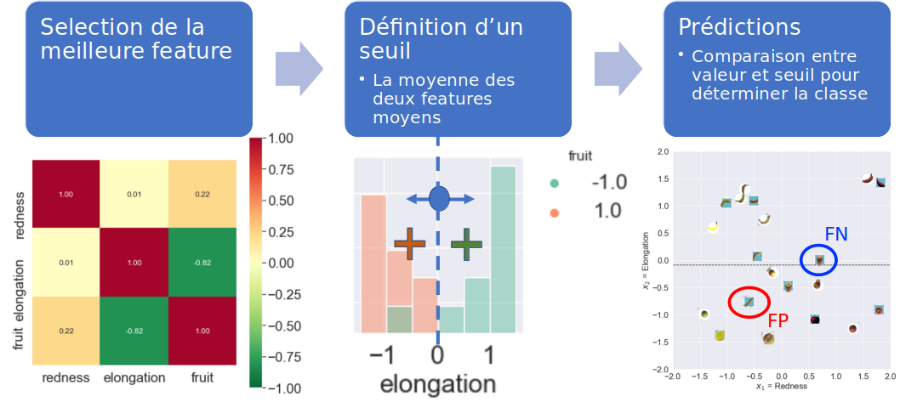
Exemple : le classificateur une règle (OneR: one rule):
on prend la décision de classe selon un seul attribut
vous pouvez implémenter votre propre OneR en TP dans la feuille classificateurs.
Arbres de décision#
Modèle avec des décisions imbriquées:
chaque nœud teste une condition sur un attribut
Exemple sur les feuilles d’Iris:
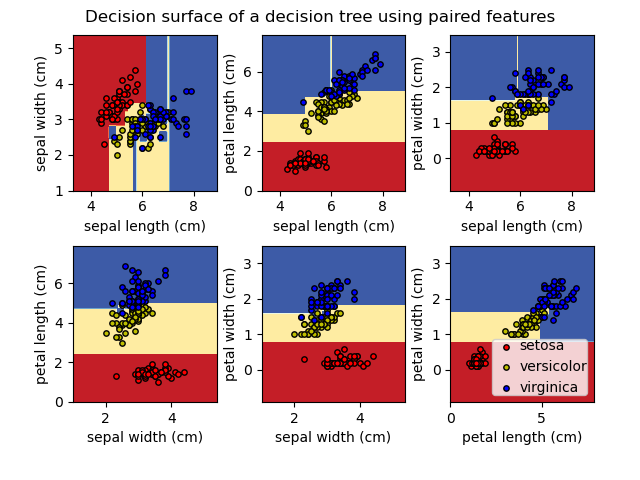
Avantages: interprétable; permet de traiter des attributs discrets, rééls et/ou binaires
Défauts: faibles propriétés de généralisation
L’implémentation est trop complexe pour ce cours (coté optimisation); l’utilisation est possible
from sklearn import tree
tree_iris = tree.DecisionTreeClassifier()
tree_iris.fit(Xtrain, Ytrain)
#prédictions
Ytrain_predicted = tree_iris.predict(Xtrain)
Ytest_predicted = tree_iris.predict(Xtest)
# Calcul des erreurs
e_tr = error_rate(Ytrain, Ytrain_predicted)
e_te = error_rate(Ytest, Ytest_predicted)
print("CLASSIFICATEUR De L'ARBRE DE DECISION")
print("Training error:", e_tr)
print("Test error:", e_te)
On parle d’arbre car les décisions peuvent etre représentées comme telles
les étiquettes se trouvent aux feuilles (une classe peut etre définie par plusieurs feuilles)
import matplotlib.pyplot as plt
plt.figure(figsize=(16,16))
tree.plot_tree(tree_iris, fontsize=10)
plt.show()
# gini : mesure de l'impureté du jeu de données
Réseaux de neurones artificiels ou perceptron#
Les réseaux de neurones artificiels :
Une modélisation mathématique du traitement de l’information par les neurones du cerveau
Le Perceptron, 1er réseau par F. Rosenblatt (1957).#
une seule couche
capacité de modélisation limitée
Composition
une couche d’entrée avec \(n\) neurones: pour chaque neurone \(i\), optimisation des poids \(w_i\)
une couche interne : les \(n\) neurones sont connectés via une fonction d’activation
une couche de sortie : un neurone qui calcule la fonction de décision
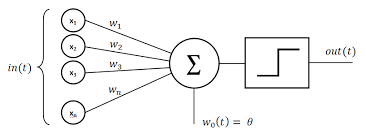
Fig. 3 https://commons.wikimedia.org/wiki/File:Perceptron_moj.png#
Entraînement
Le perceptron va s’entraîner en prenant un paquet d’images d’entraînement, prédire leurs étiquettes et changer les poids du réseau si la prédiction est fausse.
La prédiction (de l’étiquette) se fait selon la valeur de (décision) : \(D = \sum w_i * x_i + \theta\)
1 : si D > 0.0
-1 : sinon
Quand s’arreter ?
le nombre d’itérations ou d’époques (epochs) est un hyperparamètre du modèle qu’on peut fixer (paramètre max_iter dans la classe Perceptron de sklearn.linear_model)
quand on n’améliore plus la précision du modèle (on fait toujours le même nombre d’erreur, paramètre tol)
from sklearn.linear_model import Perceptron
iris_perceptron = Perceptron(tol=1e-3, random_state=2, shuffle=True, max_iter=100)
# *tol* est un autre critère d'arret
# Si loss <= previous_loss - tol alors on n'améliore pas le modèle
# en changeant les poids: on s'arrete.
#shuffle et random_state sont fixés afin d'avoir un exemple reproductible, comme une seed
iris_perceptron.fit(Xtrain, Ytrain)
#prédictions
Ytrain_predicted = iris_perceptron.predict(Xtrain)
Ytest_predicted = iris_perceptron.predict(Xtest)
# Calcul des erreurs
e_tr = error_rate(Ytrain, Ytrain_predicted)
e_te = error_rate(Ytest, Ytest_predicted)
print("CLASSIFICATEUR DU PERCEPTRON")
print("Training error:", e_tr)
print("Test error:", e_te)
# seulement 33% des données d'entrainement sont bien apprises: sous apprentissage ?
Le perceptron à couches multiples MLP#
Depuis les modèles de perceptron ont été raffinés. On parle de perceptron à plusieurs couches (MLP, multi layer perceptron) s’il possède:
une couche d’entrée,
des couches cachées.
une couche de sortie (nos classes).
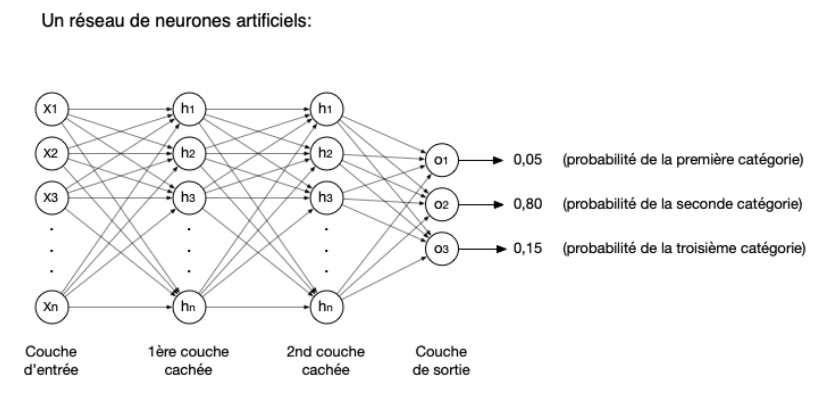
Fig. 4 https://www.lisn.upsaclay.fr/~tsanchez/activite_ia/#entrainement#
Un MLP peut avoir un nombre variable de couches cachées ainsi qu’un nombre variable de neurones par couche cachée.
Un MLP a au moins un hyperparamètre supplémentaire par rapport à ce qu’on a vu juste avant:
la taille du paquet d’images pris à chaque itération (batch size).
Elle varie entre 1 (entrainement séquentiel) et le nombre d’entités à classer (on parle de full batch). Entre ces deux valeurs, on parle de mini batch.
En fait, dans le cas du Perceptron de sklearn.linear_model, on travaille en full batch.
Retour sur l’exemple de pommes/bananes avec Marcelle#
Performance d’un perceptron multi-couches sur l’exemple de la semaine 3 (pomme verte-clémentine): Marcelle.
Autres classificateurs#
Qu’on ne détaillera pas.
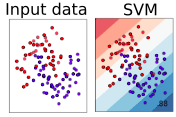
SVM Machines à vecteurs de support
Les SVM (support vector machines) optimisent la séparation des données de sorte que la frontière de décision ait la marge la plus large possible.
Méthodes à noyaux
Elles utilisent un classificateur linéaire pour résoudre un problème non linéaire après une transformation de l’espace des données en un espace de plus grande dimension. Ce changement de dimension est appelé le kernel trick (astuce du noyau), dévelopé entre autres au début des années 90 par Isabelle Guyon (professoresse ici) et d’autres.
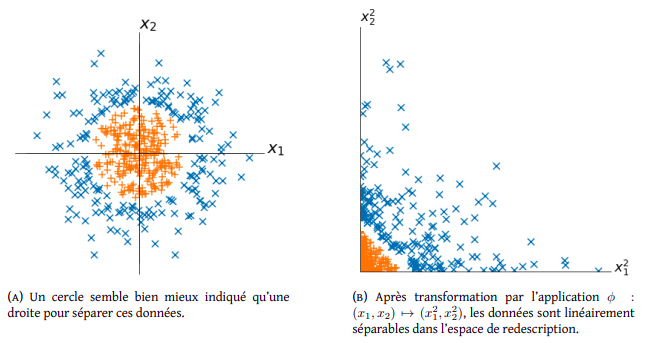
Fig. 5 http://cazencott.info/dotclear/public/lectures/IntroML_Azencott.pdf#
et plein d’autres
Conclusions#
Présentation de différents classificateurs
Basé sur les exemples (example based)
KNN
Parzen windows
Basé sur les attributs (feature based)
Une règle (OneR)
Arbres de décision
Perceptron
Python
Utilisation de la librairie
scikit-learn
Perspectives#
CM6
Préparation des données en entrée: spécificité des images
Biais dans les données
TP5
Fin du projet (appliquer au moins un classificateur tel que le KNN)
Rendu avant Mardi 27 février 23h59.
On corrigera la dernière version déposée sur GitLab avant cette date limite
Images
Pour le projet 2 vous ferez de la classification de vos propres images
Faites la feuille sur le choix de mes images pendant les vacances scolaires. Nous passerons valider votre jeu de données lors du TP6 (à la rentrée).