Ctrl+K

Cours 6: Traitement d’images

Cours 6: Traitement d’images#


Fanny Pouyet
L1 Informatique
Janvier - Avril 2024

Précédemment

  • Chaîne de traitement d’analyse de données

  • Application aux images : extraction d’attributs

  • Classificateurs

Cette semaine

  • Préparation des données : traitement d’images

Mise en contexte#

Pour le moment nous avons traité des images «parfaites» pour notre problème:

  • images toutes la même taille,

  • images carrées,

  • fond blanc,

  • objet d’étude centré.

Dans la suite du cours et pour votre Projet 2, vous allez étudier des images imparfaites, que vous aurez vous même prises:

  • fond «complexe»,

  • objet pas forcément centré,

  • images volumineuses,

  • tailles variables (résolution, …).

Aujourd’hui nous allons voir comment traiter ces images pour pallier à ces difficultés. Vous appliquerez ces méthodes lors du TP6

Les grandes étapes du traitement#

  1. Transformation d’une image en image carrée

  2. Extraction de l’objet

  3. Recadrage et centrage de l’image

  4. Réduction de la résolution

# Automatically reload code when changes are made
%load_ext autoreload
%autoreload 2
from PIL import Image, ImageDraw, ImageFont
import matplotlib.pyplot as plt
from scipy import signal

from utilities_cours_correction import *
from intro_science_donnees import *

Lors de la séance 6 nous allons traiter cette image:

img

Transformation en image carrée#

Nous allons la transformer en image carrée à l’aide de la méthode crop de PIL. Crop veut dire rogner en anglais.

img_carree = img.crop(box=(x_gauche, y_haut, x_droite, y_bas))
img_carree

Extraction de l’objet#

Comment extraire le smiley ?

Filtre pixel-à-pixel#

On peut regarder chaque pixel et déterminer s’il fait partie de l’objet ou bien de l’arrière plan. S’il est jaune, il appartient à l’objet! Pour cela trois étapes:

  1. En TP vous commencerez par construire la fonction yellowness_filter. Elle renvoie l’intensité de jaune pour chaque pixel. En RGB, le jaune \(y\) (pour yellow) se calcule comme suit:

    \(y = r + g -b \)

    La formule \(r+g-b\) est un produit scalaire \(v.w\) entre le vecteur \(v = (r,g,b)\) et le vecteur \(w=(1,1,-1)\).

  1. Puis vous créerez la fonction color_correlation_filter qui calcule pour chaque pixel d’une image, sa corrélation avec une couleur donnée (dans notre exemple le jaune).

  1. En appliquant un seuil à la sortie de cette fonction vous obtiendrez une matrice de booléens : True si le pixel appartient à l’objet, False sinon.

plt.imshow(foreground, cmap='gray');
foreground

Recadrage#

Ensuite on cherchera à recadrer l’image. On commencera par calculer son barycentre.

Définition du barycentre : Le barycentre est le centre de gravité d’un objet.

« Tout corps pesant a un centre de gravité bien défini en lequel tout le poids du corps peut être considéré comme concentré. » Archimède.

Par exemple, pour le disque c’est son centre, pour un triangle l’intersection entre les trois médianes

On effectuera un nouveau rognage (crop) centré autour du barycentre

Réduction de la résolution#

Parfois certaines images sont trop volumineuses et on peut ainsi vouloir réduire leur résolution.

En TP nous verrons comment passer d’une image 256x256 en 128x128.

Que se passe-t-il quand on sous-echantillonne des pixels ?

Il n’y a pas de contours lisses, ceux ci sont remplacés par des «escaliers» (on parle de crénelage)

plt.figure(figsize=(12,12)) 
plt.subplot(1,3,1)    
plt.imshow(resolution256x256)
plt.title("Résolution 256x256", fontsize=18) 
plt.subplot(1,3,2)    
plt.imshow(resolution64x64)
plt.title("Résolution 64x64", fontsize=18) 
plt.subplot(1,3,3)    
plt.imshow(resolution8x8)
plt.title("Résolution 8x8", fontsize=18)

Comment gérer le bruit?

On peut échantillonner la couleur des pixels à la limite des zones distinctes (l’objet et l’arrière plan par exemple) puis on remplace ces pixels par le pixel « moyen » de ses voisins. L’image sera plus floue mais ne présentera plus cet aspect d’escalier.

plt.figure(figsize=(12,12)) 
plt.subplot(1,3,1)    
plt.imshow(resolution256x256)
plt.title("Résolution 256x256 ", fontsize=18) 
plt.subplot(1,3,2)    
plt.imshow(resolution64x64_lisse)
plt.title("Résolution 64x64 lissé", fontsize=18) 
plt.subplot(1,3,3)    
plt.imshow(resolution8x8_lisse)
plt.title("Résolution 8x8 lissé", fontsize=18)

Lissage par convolution#

Convolution d’images : En traitement d’images, une matrice de convolution ou noyau est une petite matrice utilisée pour le floutage, l’amélioration de la netteté de l’image, le gaufrage, la détection de contours, et d’autres. Tout cela est accompli en faisant une convolution entre le noyau et l’image.

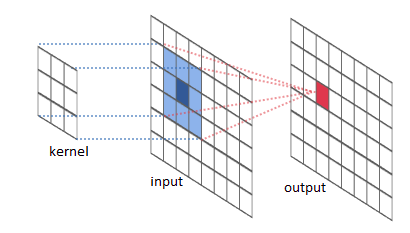
media/convolution.png

Fig. 6 http://mathinfo.alwaysdata.net/2016/11/filtres-de-convolution/#

Convolution : Chaque pixel de la nouvelle image est obtenu en multipliant le pixel d’origine et ses voisins par des coefficients (poids ou weight) donnés par une matrice appelée le noyau (kernel).
La convolution consiste à filtrer nos données et à étudier le résultat.

Exemple mathématique: le résultat correspond au produit de convolution de la fonction rouge sur la fonction bleue. C’est l’intégrale (l’aire jaune) en chaque point de la fonction bleue quand on lui applique la rouge.

https://upload.wikimedia.org/wikipedia/commons/6/6a/Convolution_of_box_signal_with_itself2.gif

Fig. 7 Source : wikimedia#

Nous verrons en TP:

  • le filtre de Gauss : convolution avec une fonction de Gauss. L’idée est de donner plus de poids aux pixels voisins qui sont proches du pixel central, selon une distribution gaussienne. La taille du noyau et l’écart type de la distribution gaussienne sont deux paramètres qui influent sur le degré de lissage.

  • le lissage itératif (avec un noyau \(3\times3\)): On définit un noyau ker et on va appliquer le calcul de lissage plusieurs fois de suite. L’idée est que chaque itération supplémentaire augmente l’effet de lissage, étendant l’influence des pixels au-delà du voisinage immédiat couvert par le noyau 3x3.

ker

# l'objet foreground_cropped_clean sera créé en TP
plt.imshow(foreground_cropped_clean, cmap='gray');

Traitement au bord : Comment faire pour les pixels aux bords ?

  • Enroulage (Wrap) : Les valeurs sont récupérées des bords opposés.

  • Extension : Le pixel le plus près du bord est dupliqué pour donner des valeurs à la convolution.

  • Miroir : L’image est reflétée sur les bords.

  • Crop : Tout pixel demandant l’utilisation de pixel en dehors de l’image n’est pas utilisé

Extraction de l’objet#

On peut maintenant extraire uniquement l’objet

smiley = transparent_background_filter(img_crop, foreground_cropped_clean)
smiley

Conclusion intermédiaire#

À cette étape, nous avons:

  • cadré;

  • filtré le jaune et identifié l’image;

  • recadré et centré l’image;

  • diminué la résolution et lissé;

  • extrait l’image

image_grid(images)

Extraction des contours#

Comment feriez vous pour extraire les contours de l’objet ?

Ici, on va calculer la différence entre chaque pixel et son voisin de gauche (c’est aussi de la convolution !).

  • S’ils sont tous les deux en arrière-plan ou bien dans l’objet alors la différence est 0.

  • Sinon, la différence est -1 ou 1, et alors on est sur le contour.

Pour ce calcul, on perd une bande de 1 pixel en largeur; pour conserver l’image carrée, on supprimera aussi une bande de 1 pixel en hauteur.

# Mat est la matrice de booléens obtenue après lissage
# Mat[:-1, 1:] : on enlève la dernière ligne et la première colonne
# Mat[:-1, :-1] : on enlève la dernière ligne et la dernière colonne

contour_horizontal = np.abs(Mat[:-1, 1:] - Mat[:-1, :-1])
plt.imshow(contour_horizontal, cmap='gray');

Superposition d’images#

Superposer deux images revient a remplacer les pixels d’une image par ceux d’une autre image. Remplacons ici, un oeil par une banane.

Prenons une image de banane des TP précédents. Cette image fait 32x32 pixels, ce qui est beaucoup plus petit que notre smiley qui fait 256x256! Dans le cas inverse nous devrions réduire la résolution avant l’incorporation.

banana = fruits.iloc[19]
M = np.array(smiley)
plt.imshow(M);

B = np.array(banana)
i = 106
j = 100
P = M[i:i+32, j:j+32]
F = foreground_filter(banana)
P[F] = B[F]
M[i:i+32, j:j+32] = P

j = 136
M[i:i+32, j:j+32] = P


plt.imshow(M);

Réalisation d’une animation#

En fin de TP, vous assemblerez toutes ces images pour faire un gif!

Remarques conclusives et domaine de la vision par ordinateur#

Aujourd’hui nous avons vu comment traiter des images :

  • cadrage et centrage;

  • filtrage;

  • changement de résolution par convolution;

  • extraction de l’image et manipulation;

  • superposition d’images;

  • animations.

Ces manipulations peuvent aller beaucoup plus loin; c’est le domaine de recherche de la vision par ordinateur (computer vision). Elle vise à:

  • reconnaître des images

  • les comprendre

  • traiter les informations qui en découlent

Un des objectifs de ce domaine est de comprendre et reproduire l’oeil humain, et plus généralement le système visuel humain. Connaissez vous des exemples d’applications de ce domaine ?

  • Mouvements et reconnaissance d’activités

Reconnaissance d'activités en vidéo (voir à partir d’1min45)

  • Voitures autonomes

    Identification des piétons et planification de leur intention

    http://wider-challenge.org/img/2019/portfolio/pedestrian.jpeg
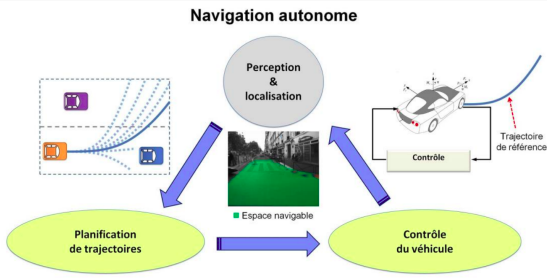
media/navigationautonome.png

Fig. 8 Source : Thèse de Marin Toromanoff, Septembre 2021, tel-03347567#

  • Biomédical

    Classification de grains de beauté, analyses d’imagerie médiale (IRM, scanners etc), reconnaissance d’espèces de bactéries

dataset_dir = os.path.join(data.dir, 'Melanoma')
gdb = load_images(dataset_dir, "*.jpg")
image_grid(gdb, titles=gdb.index)

Perspectives#

CM7: Deep Learning et classification d’images

CM8: Retour sur les classificateurs et l’évaluation des performances

CM9: Éthique et déontologie de l’IA

TP6

  • Traitement d’images (en vue du projet 2)

  • Rendu obligatoire avant Mardi 5 mars 23h59.

  • Vérification de la pertinence du jeu de données pour le projet 2

Contenu