Cours 4: Construction et sélection d’attributs#
\(\newcommand{\var}{\operatorname{var}}\) \(\newcommand{\Proba}{\operatorname{Proba}}\)
Précédemment
Définition et objectif de la science des données
Introduction à la librairie Pandas, Numpy, Matplotlib, Sklearn
Visualisation des données
Chaine de traitement en analyses des données
Cette Semaine
Extraction de features à partir d’images
Votre propre jeu de données
Extraction et sélection d’attributs : redness et elongation#
On va voir comment extraire la rougeur et l’élongation d’images en Python.
Lors de vos projets, vous serez amenés à adapter ce code à la spécificité de votre jeu de données.
En Python, nous utiliserons la bibliothèque PIL et Matplotlib
Librairie PIL#
PIL (Python Imaging Library) est une bibliothèque de traitement d’image de formats tels que PNG, JPEG, TIFF etc, qui utilise le principe d’images matricielles:
un pixel = un élément d’une matrice.
Une image en couleur contient plusieurs bandes de données (les 4 bandes RGBA vu précédemment par exemple).
PIL permet de filtrer, redimensionner, tourner, transformer les images. Grâce aux bandes on peut également agir indépendamment sur l’une ou l’autre.

Pixels RGBA#
Red, Green, Blue, Alpha (transparence)
Pixels RGBA:
Les bandes RGB varient de 0 à 255 (vu en TP2);
la bande A varie de 0 (transparent) à 255 (opaque)
Plus le chiffre est élevé plus la couleur est forte.
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
import os
#On charge l'image : étiquette de la librairie PIL
image = Image.open("media/pil.png")
#Exemple pour transformer l'image en noir et blanc
imageNB = image.convert('L')
arrNB = np.asarray(imageNB)
#matplotlib prend en entrée des array
plt.imshow(arrNB, cmap='gray', vmin=0, vmax=255)
# Manipulation des bandes, on échange les intensités de rouge, vert, bleu
# On obtient 4 sous matrices
r, g, b, a = image.split()
# on change l'ordre !
image_ordered = Image.merge("RGBA", (b, r, g, a))
plt.imshow(image_ordered)
Distinction entre l’objet et l’arrière plan#
Avant d’étudier les attributs de nos images, on souhaite extraire objet (le foreground) de l’arrière-plan (background). Ce dernier pourrait en effet influencer nos estimateurs.
Dans nos exemples (pommes et logo PIL):
# Hack: select which bytecode file to use for utilities_cours_correction depending on Python's version
import sys
ver = ''.join(str(i) for i in sys.version_info[:2])
!cp __pycache__/utilities_cours_correction.cpython-{ver}.pyc utilities_cours_correction.pyc
from utilities import *
from utilities_cours_correction import *
from intro_science_donnees import *
dataset_dir = os.path.join(data.dir, "ApplesAndBananasSimple")
# Reload code when changes are made
%load_ext autoreload
%autoreload 2
carte_RGB(image)
Observation : l’arrière plan est clair voire blanc :
beaucoup de rouge,
de vert et
de bleu.
Stratégie :
on choisit un seuil (threshold)
chaque pixel dont le rouge, le bleu et le vert est > ce seuil appartient à l’arrière-plan.
# Transform img into a numpy dataframe
M = np.array(image)
# create a dataframe (same size as each layer of M) with the lowest intensity for the RGB layers
rgb_minimal = np.min(M[:,:,0:3], axis=2)
# threshold for the background/forground distinction
threshold_background = 250
# M_background is a T/F matrix whether the pixel belongs to the background
M_background = (rgb_minimal >= threshold_background)
print(M_background)
img_background = Image.fromarray(M_background)
plt.imshow(img_background)
Objectif en TP#
Implémenter une fonction
foreground_filter()prend comme paramètre le seuil (threshold)
renvoie une matrice T/F selon que le pixel appartienne à l’objet (foreground) ou pas
On peut alors utiliser foreground_filter() pour extraire notre objet (foreground) et rogner l’arrière-plan.
La fonction transparent_background_filter() transforme tous les pixels du background en transparents.
from typing import Callable, List, Optional, Iterable, Union
# Fonction transparent_background_filter() qui prend en entrée
# soit une img soit une dataframe et le seuil (theta)
def transparent_background_filter(
img: Union[Image.Image, np.ndarray], theta: int = 150
) -> Image.Image:
"""Create a cropped image with transparent background."""
# F est donc une matrice T/F selon que le pixel soit
# dans le foreground ou pas
F = foreground_filter(img, theta=theta)
# on transforme l'image en matrice RGBA
M = np.array(img)
# N est la nouvelle image rognée, on commenca par recopier
# les couches R, G et B
N = np.zeros([M.shape[0], M.shape[1], 4], dtype=M.dtype)
N[:, :, :3] = M[:, :, :3]
# On modifie la couche d'opacité, A. On met:
# 0 pour le background (si F[i,j] = False
# et False peut etre lu comme 0)
# 255 pour le foreground (F[i,j] = True
# et True peut etre lu comme 1)
N[:, :, 3] = F * 255
return Image.fromarray(N)
Extraction de la rougeur (retour à l’exemple pommes/bananes)#
les pommes sont plutôt rouges
les bananes sont jaunes (généralement)
On peut distinguer ces fruits selon leur rougeur, c’est-à-dire la différence entre l’intensité moyenne de la bande rouge de notre objet et celle de la bande verte. Une image avec une forte rougeur aura beaucoup de rouge et peu de vert.
apple = load_images(dataset_dir, "a01.png")[0]
print(redness(apple))
extraction_objet(apple)
banana = load_images(dataset_dir, "b01.png")[0]
print(redness(banana))
extraction_objet(banana)
Objectif en TP#
Vous implémenterez la fonction redness().
Pour une image:
Extraction de la matrice des rouges et des verts (M[:,:,0] et M[:,:,1] resp.)
Transformation en nombre à virgules (floating numbers) pour faire des calculs.
Extraction de l’objet (foreground_filter())
Calcul de la redness d’une image
Calcul de la moyenne des rouges
Calcul de la moyenne des verts
Différence
Retourne la différence
Extraction de l’élongation#
les pommes sont rondes
les bananes sont allongées
Elongation: Ratio de la longueur sur la largeur de l’objet. Une pomme ronde aura la largeur \(\approx\) la longueur donc une élongation proche de 1.
# Build the cloud of points defined by the foreground image pixels
dataset_dir = os.path.join(data.dir, 'ApplesAndBananasSimple')
banana=load_images(dataset_dir, "b01.png")[0]
#fonction fournie
cloud(banana)
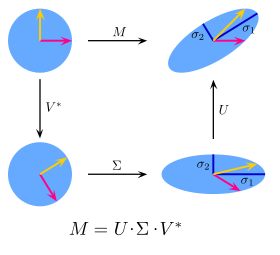
On va voir comment calculer l’élongation sachant que les fruits peuvent avoir différentes orientations et qu’il peut y avoir du bruit. Pour ce faire on va décomposer l’object en valeurs singulières
Singular vector decomposition#
La SVD est une méthode mathématique de factorisation de matrices. Elle permet d’identifier les axes d’un nuage de points pour lequel on a la plus grande variation, par une série de transformations linéaires.
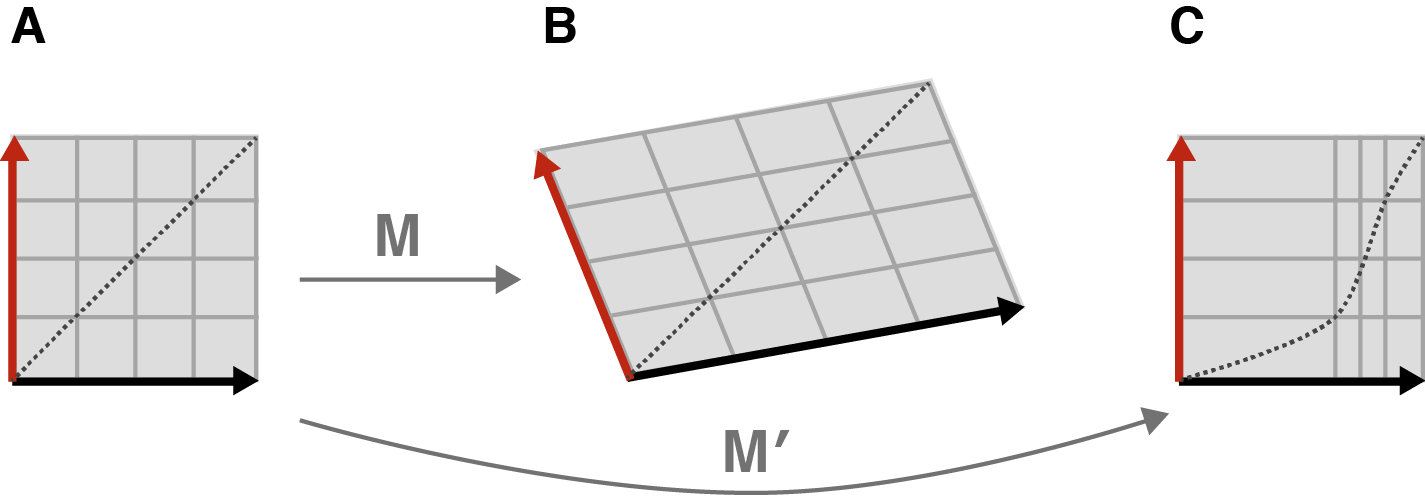
Transformations linéaires/non-linéaires
Une transformation est linéaire ssi les coordonnées des points après la transformation sont une combinaison linéaire (addition, multiplication) des coordonnées avant transformation. La même formule s’applique pour tous les points.
M est linéaire
M” n’est pas linéaire
En pratique:
on convertit l’image en un nuage de points (les coordonées des pixels de l’image)
on centre l’image
on applique l’algorithme de SVD
puis, on extrait l’axe 1 et 2 qui correspondent aux deux axes orthogonaux pour lesquels on a le plus de variation
on calcule l’élongation
def elongation(img: Image.Image) -> float:
"""Extract the scalar value elongation from a PIL image."""
F = foreground_filter(img)
# Build the cloud of points given by the foreground image pixels
xy = np.argwhere(F)
# Center the data
C = np.mean(xy, axis=0)
Cxy = xy - np.tile(C, [xy.shape[0], 1])
# Apply singular value decomposition
U, s, V = np.linalg.svd(Cxy)
return s[0] / s[1]
Objectif en TP#
Pour les bananes/pommes
implémenter et calculer l’attribut de rougeur
Calculer l’attribut d’élongation
Pour votre jeu de données
les appliquer
Autres attributs plus généraux#
Cas « difficiles » ?
Parfois les 2 catégories n’auront pas de différences de couleur (redness) ni de forme (elongation).
images = load_images(os.path.join(data.dir, 'Smiley'), "*.png")
image_grid(images, titles=images.index)
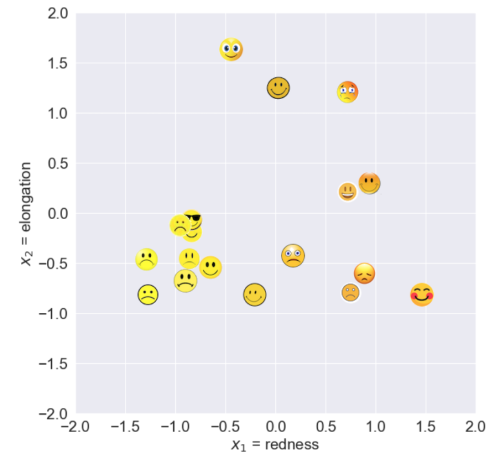
Pourtant, les smiley contents sourient et les smiley pas contents ne sourient pas, c’est simple de les distinguer !
1ère méthode : Matched filters#
On peut calculer les smiley moyens du training set:
Pour chaque classe (notée A et B), on calcule un template (le modèle):
on transforme les images en NB
on calcule la moyenne de noir qu’on a pour chaque pixel
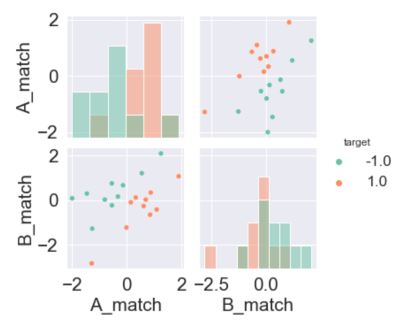
Pour chaque image test, on calcule sa corrélation avec les 2 modèles

Fig. 1 Deux exemples de correlation#
On représente les liens entre nos jeux de données test et nos modèles
from numbers import Number
def grayscale(img: Image.Image) -> np.ndarray:
"""Return image in gray scale"""
return np.mean(np.array(img)[:, :, :3], axis=2)
class MatchedFilter:
''' Matched filter class to extract a feature from a template'''
def __init__(self, examples: Iterable[Image.Image]):
''' Create the template for a matched filter; use only grayscale'''
# Compute the average of all images after conversion to grayscale
M = np.mean([grayscale(img)
for img in examples], axis=0)
# Standardize
self.template = (M - M.mean()) / M.std()
def show(self):
"""Show the template"""
fig = Figure(figsize=(3, 3))
ax = fig.add_subplot()
ax.imshow(self.template, cmap='gray')
return fig
def match(self, img: Image.Image) -> Number:
'''Extract the matched filter value for a PIL image.'''
# Convert to grayscale and standardize
M = grayscale(img)
M = (M - M.mean()) / M.std()
# Compute scalar product with the template
# This reinforce black and white if they agree
return np.mean(np.multiply(self.template, M))
#Comment utiliser MatchFilter ?
# on match avec les 10 premières images : celles qui sourient
filtre_sourire = MatchedFilter(images[:10])
#on regarde le filtre moyen
#display(filtre_sourire.show())
# on calcule la correlation moyenne entre une figure à tester et le filtre moyen
print("MATCH SOURIRE \n Pour un sourire :", filtre_sourire.match(images[9]))
print("Pour un smiley triste :" , filtre_sourire.match(images[19]))
# il faudrait encore calculer la corrélation moyenne avec le filtre moyen des smileys tristes
# puis comparer les ratios pour savoir à quelle classe appartient notre smiley !!
Objectif du TP#
Utiliser MatchFilter si besoin sur votre jeu de données
Calculer les pairplots/autres représentations pour analyser vos données
2ème méthode : Analyse en Composantes Principales (PCA ou ACP)#
Dans les cas généraux, le nombre de variables pour représenter les données est très élevé.
Pour nos (petites) images, on a 4096 variables
Intuitivement, plus on a de variables mieux c’est
Mais aussi, plus on s’emmêle les pinceaux (exemple: 4096 éléments vs. 2 attributs)
Stratégie : On peut extraire les composantes principales de nos images comme des attributs
Intérêt: extraire les composantes principales d’une image#
Visualiser les données
filtration des outliers (données aberrantes)
Réduire les coûts algorithmiques
mémoire
temps de calcul
identifie la redondance des variables
Améliorer de la qualité d’apprentissage des modèles par
sélection (choix de qq pixels) ou
extraction de variables
Analyse en Composantes Principales (ACP)#
Extraction de variables = création de m nouvelles variables à partir des p initiales, \(m << p\) (redness/elongation sont des combinaisons linéaires des 4096 éléments).
Méthode classique ACP : Représentation des données afin de maximiser la variance selon les nouvelles dimensions (comme la SVD). Cette méthode est classiquement utilisée afin de distinguer les classes. Ici on l’utilise pour extraire des attributs = les axes principaux
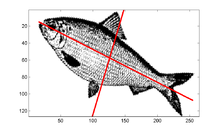
Fig. 2 https://fr.wikipedia.org/wiki/Analyse_en_composantes_principales#
Différence entre SVD et ACP#
La SVD transforme linéairement l’ensemble de la matrice et détermine l’ensemble des dimensions indépendantes
L’ACP ne gardent que les composantes principales
On peut utiliser la SVD pour trouver l’ACP en tronquant les vecteurs de base les moins importants dans la matrice SVD d’origine.
En pratique, la classe PCAFilter est fournie.
class PCAFilter:
"""PCAFilter
Similar to matched filter, but using one of the principal
components of the input images (in grayscale) instead of their
average.
"""
def __init__(self,
examples: List[Image.Image],
num: int = 0):
# Create the data matrix:
# each image contributes a column vector made of its pixels
# in grayscale
X = np.array([grayscale(img).ravel()
for img in examples])
w, h = examples[0].size
# Standardize the columns
X = (X - X.mean(axis=0)) / (X.std(axis=0)+0.000000001)
# Extract the num-th Principal Component and convert it back
# to a grayscale image
U, s, V = np.linalg.svd(X)
self.template = np.reshape(V[num, :], (h, w))
def show(self):
"""Show the template"""
fig = Figure(figsize=(3, 3))
ax = fig.add_subplot()
ax.imshow(self.template, cmap='gray')
return fig
def match(self, img, debug=False):
'''Extract the PCA filter value for a PIL image.'''
# Convert to grayscale and standardize
M = grayscale(img)
M = (M - M.mean()) / M.std()
# Compute scalar product with the template
# This reinforce black and white if they agree
return np.mean(np.multiply(self.template, M))
Objectif du TP#
Utiliser PCAFilter si besoin sur votre jeu de données
Calculer les pairplots/autres représentations pour analyser vos données
Quelques commentaires sur les jeux de données possibles pour le projet#
images = load_images(os.path.join(data.dir, 'Farm'), "*.jpeg")
image_grid(images, titles=images.index)
dataset_dir = os.path.join(data.dir, 'Hands')
images = load_images(dataset_dir, "*.jpeg")
image_grid(images, titles=images.index)
images = load_images(os.path.join(data.dir, 'ZeroOne'), "*.png")
image_grid(images, titles=images.index)
feuilles d’arbres ou plante pour reconnaitre l’espèce (voir plantnet)
animaux
etc.
Conclusion#
Comprendre, distinguer et utiliser les différentes notions:
vraie moyenne de la population, moyenne de l’échantillon
variance, ecart-type
intervalles de confiance
distribution
échantillonage, bootstrap
Python
implémenter des attributs
les appliquer à un ensemble d’image
Science des données
adapter les attributs selon le problème de classification
interpréter les résultats
est-ce un bon classificateur ?
sur quelles bases distingue-t-il les classes ?
Perspectives#
CM5
Introduction aux différentes catégories de classificateurs en machine learning
TP4
Calcul de features
Application à votre jeu de données (préparation des données, calcul des attributs)