Cours: Initiation à la Science des Données : VI-ME-RÉ-BAR#
Précédemment
Définition et objectifs de la science des données
Découverte des bibliothèques
Pandas,Matplotlib,SeabornetStatsmodelsObservation des données
Cette semaine
Chaîne de traitement en analyse des données
Un peu d’interprétation des résultats
Remerciements: Isabelle Guyon
Chaine de traitement en analyse des données#
EXPLORATION
Observer les données : Combien d’instances a-t-on ? (CM2)
Identifier la question posée. (CM2)
Comprendre ce qu’est un attribut (feature) voire en calculer d’autres (CM3) pour répondre à la question.
VIsualisation , MEsures, RÉférences et BARres d’erreurs
VI-ME-RÉ-BAR (CM3)
OBSERVATIONS
La conclusion se fait en 2 temps: l’observation de nos résultats
INTERPRÉTATIONS
Et leur interprétation. Qu’est ce qu’on peut raconter ?
Problématique#
Nous allons aborder un problème de classification automatique d’images de fruits par apprentissage statistique (machine learning). A part l’intérêt pédagogique, quelle peut être l’utilité d’étudier un tel problème ?

Connaissez-vous l’apprentissage statistique? l’intelligence artificielle ?#
Êtes vous capable de définir ces termes?
Connaissez-vous des entreprises qui en font ? Des exemples d’application ?
Répondez au sondage sur wooclap
Une révolution très récente : ChatGPT
Une autre révolution en IA : Alphafold
Définition de l’apprentissage statistique
L’apprentissage statistique (Machine Learning), combinant statistiques et informatique, est au coeur de la science des données et de l’intelligence artificielle. L’objectif est d’obtenir une fonction prédictive à partir d’un jeu de données; ici: la classification d’images de fruits.
Applications diverses
moteurs de recherche
banque
médecine
énergie
Overview - Marcelle
Marcelle est une boîte à outil qui permet de concevoir des applications interactives d’apprentissage statistique dans le navigateur. Elle permet de programmer le flux de données (pipeline) vers les modèles et d’intéragir sur les composants du flux avec des outils interactifs (visualisations, choix des paramètres etc.). Les applications ainsi réalisées peuvent être utilisées dans des contextes variés:
Pédagogie: démonstrations et utilisation de l’apprentissage machine sans programmation.
Recherche: Conception et évaluation de nouvelles interactions avec les algorithmes de ML
Collaboration entre différents domaines. Par exemple, un médecin peut s’occuper de vérifier les données tandis qu’un chercheur en apprentissage statistique conçoit le modèle. Ils peuvent collaborer via Marcelle.
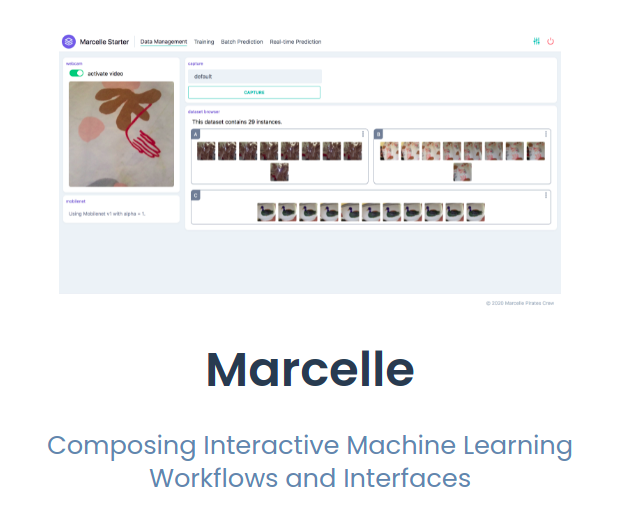
Overview - Chaîne de Traitement
Classification en direct à l’aide d’un exemple utilisant Marcelle
N.B: Marcelle est développé à Saclay par J. Francoise, B. Caramiaux et T. Sanchez. Vous pouvez aller sur le site pour tester les exemple vous même (ne fonctionne pas sur mobile): https://marcelle.dev/.
Marcelle: Composing Interactive Machine Learning Workflows and Interfaces. Annual ACM Symposium on User Interface Software and Technology (UIST ’21), Oct 2021, Virtual. DOI: 10.1145/3472749.3474734
Exemple de questions:
combien d’instance ?
pas d’infos d’attributs
notion de matrice de confusion (confusion matrix): combien on a juste / combien on a faux?
Notre jeu de données (CMs et TP3)
Nous cherchons à classer des pommes et des bananes.
from utilities_cours_correction import *
from intro_science_donnees import *
import os
# Configuration intégration dans Jupyter
%matplotlib inline
# Reload code when changes are made
%load_ext autoreload
%autoreload 2
dataset_dir = os.path.join(data.dir, 'ApplesAndBananasSimple')
images = load_images(dataset_dir, "*.png")
image_grid(images, titles=images.index)
EXPLORATION
10 images de chaque type
Label / Etiquette : l’étiquetage est le processus d’identification des données brutes. Cet étiquetage permet d’estimer l’efficacité de classification du modèle prédictif.
Quel était l”étiquette sur le jeu de données du titanic ?
Question : séparer correctement les pommes des bananes.
Attributs : les données que nous allons traiter
Etiquettes : l’appartenance aux classes de nos images
Attributs (features)#
Finalement, ce qui nous intéresse ce ne sont pas les 4096 cases mais seulement celles associées au fruit et pas au fond (au décor) à partir desquelles nous pourrons calculer des attributs explicites tels que:
la couleur;
la forme du fruit.
Lors du CM4/TP4, nous apprendrons à extraire automatiquement ce genre d’information de nos images. Pour aujourd’hui, nous supposons simplement qu’elles sont disponibles.
import pandas as pd
df = pd.read_csv("media/preprocessed_data.csv", index_col=0)
df.head()
df.shape
df.describe()
Description de la table de données:
20 instances
3 attributs dont une étiquette (ou label en anglais, lequel ?):
redness : couleur, à quel point le fruit est rouge
elongation : elongation, la ratio entre hauteur et longeur
fruit : 1 c’est une pomme, -1 c’est une banane
Observation - Objectif en TP:
Faire la description de la table, comme vu la semaine dernière :
quelle est la rougeur moyenne des pommes ? des bananes ?
quelle est l’élongation moyenne des pommes ? des bananes ?
quelles sont les échelles de valeurs des attributs ? Peut-on les comparer entre elles ?
Standardisation des données#
Motivation: On veut interpréter la valeur d’un attribut indépendamment de son échelle de valeur (range).
Géométriquement, standardiser c’est:
translater la distribution à droite ou à gauche
étendre ou compresser les données en largeur
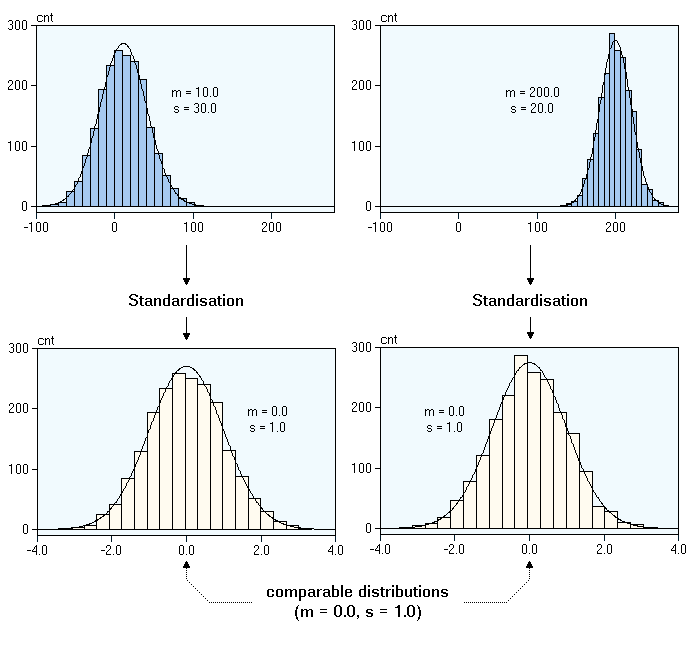
Définition:
La standardisation revient à:
centrer les valeurs d’un attribut autour de sa moyenne. Si la valeur est >0 alors elle est plus grande que la moyenne (<0, plus petite que la moyenne). Chaque attribut standardisé aura une moyenne de 0.
réduire les valeurs d’un attribut. Une valeur absolue de \(v=2\) (par exemple) veut dire qu’on est à 2 écart-types de la moyenne. Chaque attribut standardisé (chaque colonne) aura un écart-type de 1.
Mathématiquement cela revient à calculer pour chaque attribut \(X\):
\( X_{stz} = (X - \mu)/\sigma\)
La standardisation permet de mettre en évidence les valeurs aberrantes (outliers) qui auront une valeur largement différente de 0 (loin de la moyenne).
Objectifs du TP:
Standardiser les attributs selon la formule présentée (= question d’algorithmique en Python). On notera dfstz cette table. Remarquez que le label “fruit” n’a pas à être standardisé; c’est un attribut catégoriciel.
Étude de nos attributs#
En TP vous ferez:
Calcul des corrélations entre les attributs et le label
Représentation et analyse de ces relations à l’aide d’un pairplot
Observation des résultats
Interprétation: en quoi les attributs élongation/rougeur permettent de différencier les pommes des bananes ?
dfstz = (df-df.mean()) / df.std()
#on ne veut pas standardiser le label !
dfstz['fruit'] = df['fruit']
VIsualisation#
Passons ensuite à l’étape de Visualisation (nouveau). Commençons par représenter les fruits selon nos 2 attributs:
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
#Create a label with names instead of -1/1 for the legend
dfstz['Fruits'] = np.where(dfstz['fruit'] == 1, "Pommes", "Bananes")
#Make the plot, hue= "nuance" in french
sns.scatterplot(data=dfstz, x="redness", y="elongation", hue="Fruits")
Problème de classification#
Maintenant que les données ont été observées et préparées, on va répondre à notre question : peut-on séparer les pommes des bananes ?
Pour cela, on va définir un modèle qui selon des critères déterminera la nature des fruits:
le modèle permet de faire des prédictions; on veut mesurer ses performances
les critères se basent sur les attributs
la nature des fruits est encodé par l”étiquette
a. Séparation des attributs et des étiquettes#
On va séparer l’information de la table en deux sous-tables:
\(X\) contiendra les attributs pour faire des prédictions
\(Y\) contiendra ce qu’on cherche à prédire: l’étiquette
X = dfstz[['redness', 'elongation']]
Y = dfstz['fruit']
Notations \(X\) et \(Y\) :
Mathématiquement, on cherche une fonction \(f\) qui, pour chaque instance \(i\), permet de prédire \(Y_i\) en fonction des valeurs \(X_i\) des attributs.
On cherche \(f\) telle que: \(\forall i, Y_i = f(X_i)\)
b. Séparation du jeu de données#
Afin de mesurer la performance de notre modèle, on le sépare en deux groupes:
l’ensemble d’entraînement (training set) à partir duquel on ajustera (fit) les paramètres du modèle
Le modèle doit apprendre à partir d’exemples.
l’ensemble de test (test set) à partir duquel on mesurera la performance du modèle.
Le modèle est-il capable de classifier de nouveaux fruits, qu’il ne connaissait pas?
from sklearn.model_selection import train_test_split
#Separation en training et test set
train_index, test_index = split_data(X, Y, verbose = True, seed=0)
Xtrain, Xtest = X.iloc[train_index], X.iloc[test_index]
Ytrain, Ytest = Y.iloc[train_index], Y.iloc[test_index]
print("Training set:\n",Xtrain,'\n\n', Ytrain)
print("Test set:\n",Xtest,'\n\n', Ytest)
Représentation des données
#fonction fournie dans les utilities
make_scatter_plot(dfstz, images, train_index, test_index, filter=transparent_background_filter, axis='square')
REférence, Modélisation#
On peut enfin passer à la modélisation. En fait, la préparation des données, le calcul des attributs, etc. est ce qui prend le plus de temps et requiert le plus d’expertise!
Il existe pléthores de modèles. On va commencer par les \(k\) plus proches voisins mais nous en verrons d’autres au cours de l’UE.
KNN : \(k\)-Nearest Neighbors#
Le classificateur \(k\)-nearest neighbors est une méthode assez intuitive, l’objet est définit selon le label majoritaire de ses \(k\) voisins. Les résultats changent selon la valeur de \(k\) utilisée.
Le classificateur KNN est implémenté dans la bibliothèque
scikit-learn (notée sklearn) dans la classe KNeighborsClassifier
de sklearn.neighbors. En pratique cela donne:
from sklearn.neighbors import KNeighborsClassifier
#Posons :
k = 3
# Définissons le modèle KNN avec k=3
my_first_model = KNeighborsClassifier(n_neighbors=k)
# Apprentissage automatique à partir de l'ensemble d'entrainement
my_first_model.fit(Xtrain, Ytrain)
MEsure des performances#
L’ensemble de test (test set) permet de mesurer les performances en appliquant le modèle ajusté au test. Le modèle détermine si le fruit est une pomme ou pas.
Ytest_predicted = my_first_model.predict(Xtest)
La prédiction correspond-t-elle à la vérité de l’ensemble de test ?
Pour mesurer les performances de notre modèle prédictif on peut compter le nombre d’erreurs:
Faux positifs (FP) : Nombre de bananes (négatif) prises pour des pommes (positif)
Faux négatifs (FN) : Nombre de pommes (positif) prises pour des bananes (négatif)
TRUE = Pomme = 1 |
FALSE = Banane = -1 |
|
|---|---|---|
PREDICT Pomme = 1 |
TP |
FP |
PREDICT Banane = -1 |
FN |
TN |
Ceci est une matrice de confusion.
TP = vrai (true) positif; TN = vrai (true) négatif
Au total on a \(n\) prédictions et \(n= TP + TN + FP + FN\)
Le taux d’erreur \(e\) est donc:
\(e = \frac{(FP + FN)}{ n}= \frac{n_{erreurs}}{n_{prédictions}}\)
En pratique, on va comparer les labels estimés donc Ytest_predicted avec les véritables labels Ytest.
e = np.sum((Ytest_predicted != Ytest)) / len(Ytest)
e
#Strictement équivalent à
e_v2 = np.mean(Ytest_predicted != Ytest)
e_v2
On peut également calculer
La précision de la classification (accuracy), a = 1 – e
Le Balanced Error Rate, BER = 0.5 (T1 + T2)
avec T1 = Type I error = FP / (TN+FP)
et T2 = Type II error = FN / (TP+FN)
Le BER est utilisé lorsque le nombre d’échantillons par classe (pommes/bananes) est déséquilibré car on calcule la moyenne du taux d’erreur de chaque classe. Ce n’est pas le cas ici.
Objectifs en TP#
Implémenter une fonction
error_rate()pour automatiser ce calcul et l’utiliser.Calculer la précision de la classification
Représenter graphiquement les données et observer les résultats
BARres d’erreurs et significativité#
L’objectif est de répondre à la question : A quel point avons-nous confiance dans notre modèle ? Comment savoir si le modèle serait performant sur de nouvelles données ?
Cette variabilité peut être estimée par des outils comme :
l’intervalle de confiance : donne une plage où se situe probablement
la validation croisée : Permet de mesurer la performance réelle d’un modèle en le testant sur des données non vues.
C’est seulement après cette étape que nous pourrons interpréter les résultats.
Pour ce faire nous cherchons à estimer l’erreur de notre taux d’erreur. On a 2 options:
Calculer l’erreur standard 1-\(\sigma\) de notre modèle prédictif:
\(\sigma = \sqrt{\frac{e * (1-e)}{n}}\) où \(e\) est le taux d’erreur et \(n\) est le nombre de tests effectués dans une instance.
Sauriez-vous indiquer ce qui se passerait si on faisait plus de tests ?
Interprétation de l’erreur standard avec une distribution normale
Pour une distribution normale, l’erreur standard permet de définir des intervalles autour de la moyenne (\(\mu\), ici le taux d’erreur moyen) qui contiennent une proportion donnée des observations :on a :
\(P(\mu-\sigma<erreur<\mu+\sigma) = 0.68\)
\(P(\mu-2\sigma<erreur<\mu+2\sigma) = 0.95\)
Souvent vous verrez écrit : erreur = \(\mu \pm 2 \sigma\), ce qui se lit « Le taux d’erreur estimé de notre classificateur est de \(\mu\) à plus ou moins deux \(\sigma\), avec un niveau de confiance de 95% ».
Attention : La distribution normale est une approximation valide ici si n est suffisamment grand (loi des grands nombres). Ce n’est pas le cas dans nos TP !
Estimer la barre d’erreur par validation croisée CV
La méthode de validation croisée répétée permet d’estimer un intervalle de confiance pour le taux d’erreur de notre classificateur.
répéter \(N=100\) ou \(1000\) (ou encore plus) fois la séparation entre l’ensemble de test et d’entrainement;
recalculer la performance du modèle réapprenant.
On a donc \(N\) taux d’erreurs à partir desquels on peut estimer le taux d’erreur moyen.
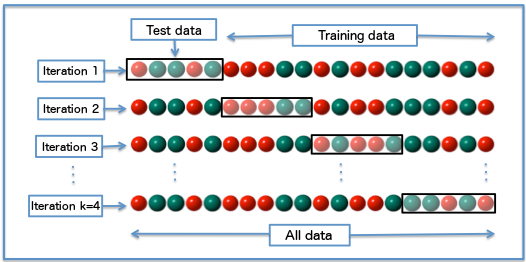
En TP et tout au long de cette UE, nous ferons de la valdiation croisée pour évaluer nos classificateurs.
Pseudo-code:
Soit B le nombre de répétitions
Soit \(n_{tr} + n_{te}\) la taille d’échantillon (sample size)
Pour chaque \(b \in B\) (boucle for):
Echantillonnage d’un training (\(n_{tr}\)) et d’un test set (\(n_{te}\))
Optimisation du modèle sur le training set actuel (model fit)
Calcul du taux d’erreur ou de l’accuracy sur le test set actuel
Calcul de la moyenne et de la variance des \(B\) taux d’erreurs.
Remarque importante: toute filtration des données effectuée avant de fitter un modèle doit être inclue dans la boucle for afin d’éviter d’introduire des biais et ainsi de surestimer la précision de notre modèle.
La distribution des \(e\) observées par rééchantillonnage se rapproche d’une courbe gaussiene définies par sa moyenne (\(\bar{e}\)) et son écart-type \(\sigma\) (voir théorème central limite en CM4)
On peut définir un intervalle de confiance de notre taux d’erreur car 95% des mesures du taux d’erreur tomberaient entre \(\bar{e}+2\sigma\) et \(\bar{e}-2\sigma\).
Retour sur les concepts#
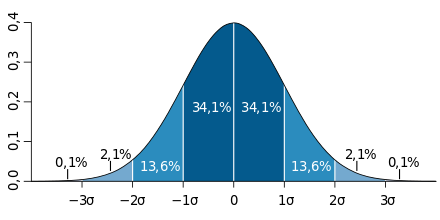
Loi Normale#
Loi normale ou courbe en cloche. Une des distributions les plus fréquentes en statistiques.
la moyenne (\(\mu\)) et la médiane sont égales
la variance vaut \(\sigma^2\)
la courbe est symétrique
95% des observations sont comprises entre \([\mu - 2 \sigma; \mu + 2 \sigma]\).
si \(\mu=0\) et \(\sigma^2=1\), on parle de loi normale centrée réduite.

Taille d’échantillon \(n\)#
Dans notre étude, la moyenne de «redness» de nos dix pommes est très probablement différente de la moyenne de «redness» de toutes les photos de pommes sur Terre.
Mathématiquement (voir le Théorème Central Limite), on distingue:
\(\mu\): la vraie moyenne de \(X\)
\(\hat{\mu} = (1/n) (\sum_{i=1}^n X_i)\): l’estimateur empirique (calculé sur seulement \(n\) exemples).
Intuitivement, la moyenne calculée sur un échantillon (\(\hat{\mu}\)) est une approximation de la moyenne vraie (\(\mu\)). Plus la taille de l’échantillon est grand, plus \(\hat{\mu}\) est proche de \(\mu\) (voir le théorème central limite pour une démonstration).
Conclusions#
Science des données
Chaîne de traitement en analyses des données:
on peut synthétiser l’information dans les images en une table
préparer les données prend du temps
L’interprétation des résultats dépend des barres d’erreurs !
Langage Python 3
sklearnpour l’apprentissage statistique et les problèmes de classificationPIL pour le traitement d’images (en détail lors du CM4)
Perspectives#
CM 4 : Construction & selection d’attributs
Extraction d’attributs a partir d’images
Votre propre jeu de données
TP 3
Observer les attributs
Calculer un modèle prédictif (prédeterminé: le 1-NN)
Calculer des barres d’erreur
TP 4 et 5 : Mini-projet
Classification d”images en binôme
Choisissez deux catégories d’images que vous aimeriez classer parmi un ensemble fourni en TP3:
canards/poulets, zeros/uns, …
il y aura 10 images par classe
Comment peut-on manipuler des images en Python ?#
Une image est un tableau de pixels
Dans le TP, un pixel de couleur est défini comme la superposition de quatre couches d’information, RGBA (Red Green Blue Alpha): trois couleurs + l’opacité (alpha).
Exemples de cartes RGB
Histogramme des couleurs
On peut aussi visualiser les données comme un histogramme. Comment le lisez vous ?
Une vraie pomme
Refaisons l’exercice avec une image d’une vraie pomme.
Des images aux dataframes
Vous apprendrez à passer d’une image à un tableau dans la feuille Manipulation d’images du TP4. Le tableau est en 3D car on a:
le nombre de pixels en largeur (32 dans notre cas)
le nombre de pixels en hauteur (32 dans notre cas)
les quatre couches: R, G, B et A
Quelle bibliothèque (qu’on a déjà mentionnée) va-t-on utiliser lors du TP3 pour manipuler ces images manipulées?
Bibliothèque :
PandasCombien de cases a-t-on par image ?