Cours 8: Evaluation des performances et Biais#
Précédemment
Chaine de traitement d’analyse de données
Application aux images : extraction de features
Classificateurs
Préparation des données : traitement d’images
Deep Learning et classification d’images
Cette semaine
Evaluation des performances dans un problème de classification d’images
Biais dans les données
Déclaration des classificateurs#
Il existe de très nombreux classificateurs d’images dans la librairie scikit-learn.
Pouvez vous en citer au moins 3 ?
Pour chaque classificateur on peut :
définir un ensemble d’entrainement et de test
utiliser les méthodes
.fitet.predictcalculer des performances
Choisir le meilleur classificateur#
Selon les classificateurs on n’obtient pas les mêmes resultats. Comment choisir le meilleur classificateur ?
Notions de sous-apprentissage et sur-apprentissage#
Ces deux notions sont liés à la granularité de la frontière de décision. Elles sont illustrées par les graphiques suivants :

Lorsque l’on entraîne un classificateur sur des données, deux comportements sont à éviter:
Lorsque à la fois les performances d’entraînement et celles de test sont mauvaises, on dit que le classificateur a sous-appris (under-fitting).
Lorsque les performances d’entraînement sont bonnes mais pas celles de test, on dit alors que le classificateur a sur-appris (over-fitting).
Question Peut-on à la fois sur-apprendre et sous-apprendre ?
Pour identifier les classificateurs qui ont un de ces deux comportements on doit définir ce qu’est une mauvaise performance.
on peut choisir un seuil
on peut comparer les performances entre classificateurs. Lors du projet 2, « mauvais » veut dire que les performances sont inférieures à la performance médiane. (Question Revenir sur la définition pratique de l’underfitting/overfitting dans ces conditions)
Comité de classificateurs#
Pour chaque image, les classificateurs font des prédictions. Et ils sont soient en accord soit en désaccord entre eux. On peut faire voter les classificateurs et choisir la classe finale après le vote.
Comité de classificateurs : classificateur dans lequel les réponses de plusieurs classificateurs sont combinées en une seule réponse. En d’autres termes, chaque classificateur vote pour l’une ou l’autre des catégories.
Avertissement
La performance du comité n’est pas forcément la meilleure solution car les classificateurs pris individuellement peuvent être meilleurs à notre tache.
Gestion de l’incertitude#
Selon le degré d’accord entre classificateurs on peut quantifier l’incertitude de nos données.

l’incertitude aléatorique : Les classificateurs du comité sont d’accord sur des probabilités
incertaines : chaque classificateur émet
une probabilité proche de [0.5, 0.5]. Elle est lié à l”ambiguïté intrinsèque de la
tâche de classification.
l’incertitude épistémique : Les classificateurs du comité sont certains de leurs prédictions,
mais ils sont en désaccord entre eux : les
classificateurs émettent chacun une probabilité confiante mais
différentes: [1.,0.], [0., 1.], [0.9, 0.1], [0.05, 0.95],
etc. Elle est
lié à l’idée de nouveauté dans les données. Cette incertitude
peut être réduite en ajoutant de nouvelles données.
Remarque
Les images avec une faible incertitude épistémique (les classificateurs sont d’accord) et une grande incertitude aléatorique (les classificateurs sont incertains de la prédiction) correspondent à des images se situant aux abords de la frontière de décision entre nos deux classes.
Incertitude aléatorique#
Pour chaque classificateur et chaque image, on estime cette incertitude en calculant l’entropie de Shanon qui est une mesure issue de la théorie de l’information.
Entropie de Shannon : mesure la quantité d’information contenu dans une source. Ici, notre probabilité d’appartenir à une classe pour l’image X:
avec \(x_i\) la probabilité de classification sur la classe \(i\).
Comportement de cette fonction avec 2 classes:
Incertitude épistémique#
Rappel: Les classificateurs du comité sont certains de leurs prédictions, mais ils sont en désaccord entre eux : les classificateurs émettent chacun une probabilité confiante mais différentes: [1.,0.], [0., 1.], [0.9, 0.1], [0.05, 0.95], etc.
Pour chaque image, on peut alors calculer l’incertitude moyenne d’une image en calculant l’écart-type pour une des classes entre les classificateurs:
où \(c\) sont les classificateurs et \(x_c\) la probabilité d’appartenir à la première classe. En effet, comme nous n’avons que deux classes l’écart-type est identique pour l’une ou l’autre.
L’incertitude épistémique de notre comité correspond à la moyenne des incertitudes des images.
Le biais dans les données: les bonnes versus les mauvaises données#
Big data#
Peter Norvig, directeur de recherche chez Google a dit en 2011: « We don’t have better algorithms, we just have more data. » A cette époque, on pensait que les méthodes d’IA pourraient résoudre tous les problèmes s’ils avaient suffisamment de données (les big data).
Etes-vous capable de remettre en cause cette assertion : qu’est ce qui pose problème ?
Cette idée simpliste à mener à des défaillances graves d’algorithmes prenant des décisions éthiquement problématiques, racistes (exemple) ou sexistes.
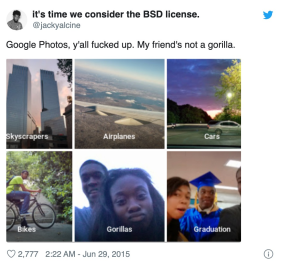
Source: twitter en 2015#
Good data#
Peter Norvig a repris sa citation et ajouté cette nuance indispensable : “More data beats clever algorithms, but better data beats more data.”
Pour l’exemple raciste ci-dessus, l’algorithme n’avait été entrainé qu’à reconnaitre des humains caucasiens (« blancs »), ratant une large diversité humaine. Les bonnes données d’entrainement doivent donc contenir une diversité représentative des données existantes.
Pour le jeu de données pommes/bananes :
Si on a 1 000 000 de photos de pommes et qu’elles sont toutes rouges, on croira que les golden (pommes jaunes) sont des bananes…
Il vaut mieux 1 000 photos variables que 1 000 000 de photos identiques ou presque identiques
Good data et absence de biais dans les données#
Définition#
En statistique, un biais engendre des erreurs systématiques qui font que les résultats d’une étude sont faussés. Cela pose problème lorsque les conclusions sont différentes de la vérité (Last, 2001)
Mathématiquement pour un paramètre, le biais d’un estimateur est la différence entre la moyenne de l’estimateur (qui est une variable aléatoire, voir CM2) et la valeur du paramètre (valeur fixe).
Il existe une multitude de biais et 2 catégories :
soit le biais provient des participants/données intrinsèques
soit de la personne effectuant les recherches
exemple avec le biais d’échantillonnage : les personnes sondées ne sont pas représentatives de la population : soit les personnes ne répondent pas toutes (biais provenant des participants) soit les personnes invitées à répondre ne représentent pas la population générale (biais provenant de la chercheuse ou du chercheur)
Il faut faire attention à ne pas introduire un biais systématique dans les données d’entrainement.
Trois exemples de biais#
Biais d’échantillonnage#
Cas pratique: lors de la seconde guerre mondiale, on analyse les impacts de balles sur les avions anglais touchés par des tirs nazis revenus à la base.
Ou doit-on renforcer la coque des avions ?
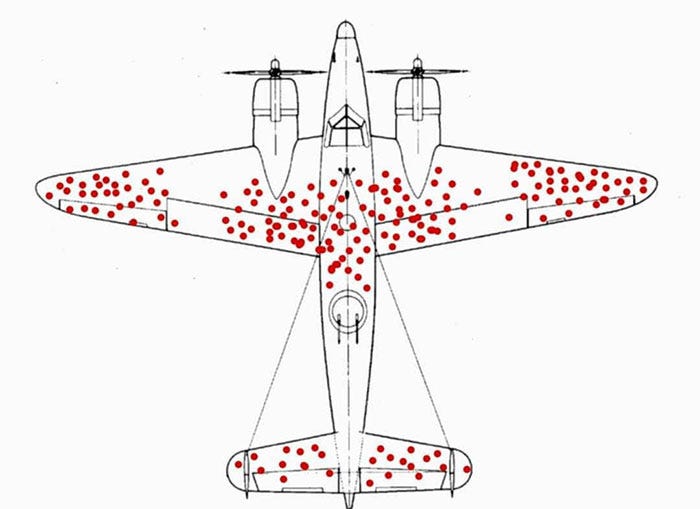
Le biais d’échantillonnage vient du fait qu’on n’analyse que les avions qui sont revenus à la base et donc qui ont continué à voler. Il faut renforcer là ou il n’y a pas d’impacts de balles !!
On ne prend que des pommes rouges alors qu’il existe des pommes jaunes (par ex. les golden) ou vertes (par ex. les granny smith).
# Automatically reload code when changes are made
%load_ext autoreload
%autoreload 2
import os
from PIL import Image, ImageDraw, ImageFont
import matplotlib.pyplot as plt
from scipy import signal
import seaborn as sns
from intro_science_donnees import data
from intro_science_donnees import *
from utilities import *
# Configuration intégration dans Jupyter
%matplotlib inline
dataset_dir = os.path.join(data.dir, 'ApplesAndBananas')
images = load_images(dataset_dir, "*.png")
redapples = [crop_image(img) for img in images[[114,115,116,118,122,124,125,133,134,135]]]
image_grid(redapples)
On ne pourra pas généraliser: ce serait risqué de considérer la couleur comme un attribut adéquat.
couleur = [crop_image(img) for img in images[[100,101,102,103,104,114,115,116,118,122,369,370,374,375,377]]]
image_grid(couleur)
Biais confondant#
Paradoxe de Simpson : on a une mauvaise corrélation entre deux variables, car on ne controle pas pour une troisième variable qui provoque la confusion.

Pour classifier des images on peut par exemple mesurer les éléments dans des contextes différents. Le contexte peut alors etre confondu avec l’élément lui-même. On ne pourra pas généraliser, si le contexte change on ne saura pas s’adapter.
exemple : Les photos d’avions dans le ciel versus de voitures sur goudron. Comment classerait-on un avion au sol ?

Biais de mesure#
Par exemple, si on ne prend que des bananes photographiées horizontalement dans le jeu de données d’entrainement, on ne pourra pas généraliser car on risque de croire que l’orientation est une information utile pour discriminer les pommes des bananes.
bananas_h = [crop_image(img) for img in images[[369,370,374,375,377,379, 387,396,401,406]]]
image_grid(bananas_h)
Correction des biais#
Comment pallier ces problèmes ?
en évitant les biais (dans le protocole de collecte des données)
en identifiant les biais et en les corrigant: on récupère les métadonnées (marque du téléphone, orientation des images, date, température, personne qui a récupéré les données etc) et on donne des noms explicites aux attributs! La correction est hors-programme mais on peut en discuter à l’oral.
Conclusions#
Deep Learning: réseau de neurones, perceptron multi-couches, CNN …
Grand jeu de données réputé difficile : ImageNet, qui sert de jeu de test
Deux exemples d’architectures de CNN qui ont marqué le domaine de la vision par ordinateur
Il existe de nombreux types de biais = tout facteur affectant la conclusion du test alors que ce n’est pas les données testées
Plus de données n’est pas forcément mieux
Perspectives#
CM9 : Impact écologique et impact sociétal de l’intelligence artificielle
QCM2: encore un quizz à faire
Comment gérer nos données étant donné nos classificateurs?#